| title | description | keywords | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
1232. 缀点成线 |
LeetCode 1232. 缀点成线题解,Check If It Is a Straight Line,包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。 |
|
🟢 Easy 🔖 几何 数组 数学 🔗 力扣 LeetCode
You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a
straight line in the XY plane.
Example 1:
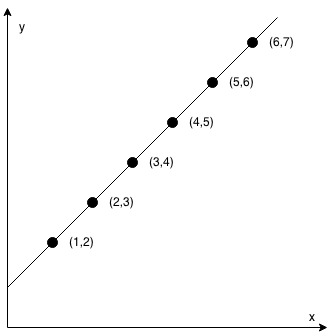
Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
Output: true
Example 2:
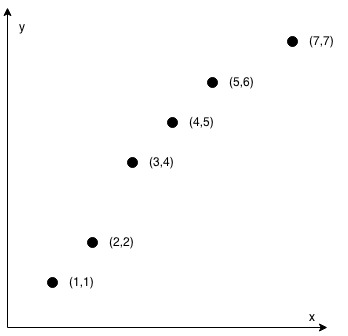
Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
Output: false
Constraints:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinatescontains no duplicate point.
给定一个数组 coordinates ,其中 coordinates[i] = [x, y],[x, y] 表示横坐标为 x、纵坐标为
y 的点。请你来判断,这些点是否在该坐标系中属于同一条直线上。
示例 1:

输入: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
输出: true
示例 2:

输入: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
输出: false
提示:
2 <= coordinates.length <= 1000coordinates[i].length == 2-10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4coordinates中不含重复的点
-
直线斜率公式:
- 对于两点
(x1, y1)和(x2, y2),斜率为:k = (y2 - y1) / (x2 - x1) - 斜率相等的充要条件是:
(y2 - y1) * dx = (x2 - x1) * dy - 其中
dx和dy是基准的横坐标和纵坐标差,避免除法计算引发精度问题。
- 对于两点
-
遍历数组:
- 使用前两个点的坐标,计算初始的
dx和dy。 - 遍历其余点,逐一验证其与基准点的斜率是否相等。
- 如果有点的斜率不同,立即返回
false;否则最终返回true。
- 使用前两个点的坐标,计算初始的
- 时间复杂度:
O(n),其中n是点的数量,遍历coordinates的所有点,每个点的计算复杂度为O(1)。 - 空间复杂度:
O(1),使用了常量级变量存储坐标差。
/**
* @param {number[][]} coordinates
* @return {boolean}
*/
var checkStraightLine = function (coordinates) {
// 基准点的坐标差
const dx = coordinates[1][0] - coordinates[0][0];
const dy = coordinates[1][1] - coordinates[0][1];
// 遍历剩余点,验证斜率
for (let i = 2; i < coordinates.length; i++) {
const x1 = coordinates[i - 1][0];
const y1 = coordinates[i - 1][1];
const x2 = coordinates[i][0];
const y2 = coordinates[i][1];
// 检查斜率是否一致
if (dx * (y2 - y1) !== dy * (x2 - x1)) {
return false;
}
}
return true;
};