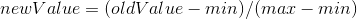第 3 章 图像分类
作者: 张伟 (Charmve)
日期: 2021/04/29
- 第 3 章 图像分类
- 3.1 数据驱动方法
- 3.1.1 语义上的差别
- 3.1.2 图像分类任务面临着许多挑战
- 3.1.3 数据驱动的方法
- 3.2 k 最近邻算法
- 3.2.1 k 近邻模型
- 3.2.2 k 近邻模型三个基本要素
- 3.2.3 KNN算法的决策过程
- 3.2.4 k 近邻算法Python实现
- 小结
- 参考文献
- 3.3 支持向量机
- 3.3.1 概述
- 3.3.2 线性支持向量机
- 3.3.3 从零开始实现支持向量机
- 3.3.4 支持向量机的简洁实现
- 3.4 逻辑回归 LR
- 3.4.1 逻辑回归模型
- 3.4.2 从零开始实现逻辑回归
- 3.4.3 逻辑回归的简洁实现
- 3.5 实战项目 3 - 表情识别
- 3.6 实战项目 4 - 使用卷积神经网络对CIFAR10图片进行分类
- 小结
- 参考文献
- 3.1 数据驱动方法
k近邻法(k-nearest neighbor, k-NN)是一种基本分类与回归方法。本章节先从机器学习的角度探讨分类问题中的 k 近邻法,然后再将其延申到图像分类的计算机视觉场景中。
k 近邻法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别,可以取多类。k 近邻法假设给定一个训练数据集,其中的实例类别已确定。分类时,对新的实例,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测。
因此,在学习掌握k近邻算法时,主要关注模型及其三要素:距离度量、k 值选择和分类决策规则。
本章节先介绍k近邻算法模型,然后讨论k近邻算法的模型及三个基本要素,最后以python代码实现讲述k近邻算法的实现方法。
k 近邻法使用的模型实际上对应于对特征空间的划分。
k 近邻算法简单、直观:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最近邻的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分为这个类。下面先叙述k近邻算法,然后再讨论其细节。
算法 3.1 (k 近邻算法)
输入:训练数据集
其中,$x_i ∈ X \subseteq R^n$ 为实例的特征向量,
输出:实例x所属的类y。
具体过程为: (1)根据给定的距离度量,在训练集T中找出与x 最近邻的k个点,涵盖这k个点的x的邻域,记作$N_k(x)$; (2)在$N_k(x)$中根据分类决策规则(如多数表决)决定x的类别y;
式(3.1)中,I为指示函数,即当 $ y_i = c_j $ 时 I 为1,否则 I 为 0;
k 近邻法的特殊情况是 k = 1的情形,称为 最近邻算法。 对于输入的实例点(特征向量)x, 最近邻算法将训练数据集中与x最邻近点的类作为x的类。
k 近邻算法没有显示的学习过程。
k 近邻算法中,当训练集、距离度量(如欧氏距离)、k值及分类决策规则(如多数表决)确定后,对于任何一个新的输入实例,它所属的类唯一确定。
距离就是平面上两个点的直线距离。
关于距离的度量方法,常用的有:欧几里得距离、余弦值(cos), 相关度 (correlation), 曼哈顿距离 (Manhattan distance)或其他。
Euclidean Distance 定义: 两个点或元组P1=(x1,y1)和P2=(x2,y2)的欧几里得距离是(如图3.1所示)。
图3.1 欧几里得距离计算
距离公式为:(多个维度的时候是多个维度各自求差)
距离的选择有很多种,常用的距离函数如下:
- 明考斯基(Minkowsky)距离
-
曼哈顿(Manhattan)距离
$$d(X,Y)=\sum\nolimits_{i=1}^{n}∣xi−yi∣$$ 该距离是Minkowsky距离在λ=1时的一个特例 -
Cityblock距离
-
欧几里德(Euclidean)距离(欧氏距离)
$$d(X,Y)=[\sum\nolimits_{i=1}^{n}∣x_i−y_i∣^2]\frac{1}{2}=(X−Y)(X−Y)T$$ 欧氏距离是Minkowsky距离在λ=2时的特例 -
Canberra距离
$$d(X,Y)=\sum\nolimits_{i=1}^{n}(x_i−y_i)(x_i+y_i)$$ -
Mahalanobis距离(马式距离) $$ d(X,M)=\sqrt{(X−M)TΣ−1(X−M)}$$
d(X,M)给出了特征空间中的点X和M之间的一种距离测度,其中M为某一个模式类别的均值向量,∑为相应模式类别的协方差矩阵。 该距离测度考虑了以M为代表的模式类别在特征空间中的总体分布,能够缓解由于属性的线性组合带来的距离失真。易见,到M的马式距离为常数的点组成特征空间中的一个超椭球面。
- 切比雪夫(Chebyshev)距离
切比雪夫距离或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各坐标数值差的最大值。在二维空间中。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为
切比雪夫距离或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各坐标数值差的最大值。在二维空间中。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为
- 平均距离
K:临近数,即在预测目标点时取几个临近的点来预测。
K值得选取非常重要,因为:
-
如果当K的取值过小时,一旦有噪声得成分存在们将会对预测产生比较大影响,例如取K值为1时,一旦最近的一个点是噪声,那么就会出现偏差,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
-
如果K的值取的过大时,就相当于用较大邻域中的训练实例进行预测,学习的近似误差会增大。这时与输入目标点较远实例也会对预测起作用,使预测发生错误。K值的增大就意味着整体的模型变得简单;
-
如果K==N的时候,那么就是取全部的实例,即为取实例中某分类下最多的点,就对预测没有什么实际的意义了;
K 的取值尽量要取奇数,以保证在计算结果最后会产生一个较多的类别,如果取偶数可能会产生相等的情况,不利于预测。
K 的取法:
-
常用的方法是从k=1开始,使用检验集估计分类器的误差率。重复该过程,每次K增值1,允许增加一个近邻。选取产生最小误差率的K。
-
一般k的取值不超过20,上限是n的开方,随着数据集的增大,K的值也要增大。
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
多数表决规则(majority voting rule) 有如下解释:如果分类的损失函数为0-1损失函数,分类函数为
那么误分类的概率是 $$ P(Y \neq f(X)) = 1 - P(Y = f(X)) $$ 对给定的实例$x∊X$,其最近邻的k个训练实例点构成集合$N_k(x)$。如果涵盖Nk(x)的区域的类别是$c_j$,那么误分类率是
要使误分类率最小即经验风险最小,就要使
如图3.2所示,有两种类型的样本数据,一类是蓝色的正方形,另一类是红色的三角形,中间那个绿色的圆形是待分类数据:
图3.2 k近邻模型决策过程
如果K=3,那么离绿色点最近的有2个红色的三角形和1个蓝色的正方形,这三个点进行投票,于是绿色的待分类点就属于红色的三角形。而如果K=5,那么离绿色点最近的有2个红色的三角形和3个蓝色的正方形,这五个点进行投票,于是绿色的待分类点就属于蓝色的正方形。
如图3.3所示,图解了一种简单情况下的k-最近邻算法,在这里实例是二维空间中的点,目标函数具有布尔值。正反训练样例用“+”和“-”分别表示。图中也画出了一个查询点xq。注意在这幅图中,1-近邻算法把xq分类为正例,然而5-近邻算法把xq分类为反例。
图3.3 一种简单情况下的k-最近邻算法
图解说明: 左图画出了一系列的正反训练样例和一个要分类的查询实例xq。1-近邻算法把xq分类为正例,然而5-近邻算法把xq分类为反例。
右图是对于一个典型的训练样例集合1-近邻算法导致的决策面。围绕每个训练样例的凸多边形表示最靠近这个点的实例空间(即这个空间中的实例会被1-近邻算法赋予该训练样例所属的分类)。
对前面的k-近邻算法作简单的修改后,它就可被用于逼近连续值的目标函数。为了实现这一点,我们让算法计算k个最接近样例的平均值,而不是计算其中的最普遍的值。更精确地讲,为了逼近一个实值目标函数$f:Rn⟶R$,我们只要把算法中的公式替换为:
示例A: 使用K-近邻算法改进约会网站的配对效果
(1) 收集数据:提供文本文件。
(2) 准备数据:使用python解析文本文件。
(3) 分析数据:使用Matplotlib画二维扩散图。
(4) 训练算法:此步骤不适用于K-近邻算法。
(5) 测试算法:使用海伦提供的部分数据作为测试样本。
测试样本和非测试样本的区别在于:测试样本是已经完成分类的数据,如果预测分类与实际类别不同,则标记为一个错误。
(6) 使用算法:产生简单的命令行程序,然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型。
将待处理的数据改变为分类器可以接受的格式。该函数的输入为文件名字符串,输出为训练样本矩阵和标签向量
def file2matrix(filename):
fr = open(filename)
#readlines()函数一次读取整个文件,readlines() 自动将文件内容分析成一个行的列表,
#该列表可以由 Python 的 for ... in ... 结构进行处理。
arrayOLines = fr.readlines()
#len() 返回字符串、列表、字典、元组等长度。
#得到文件的行数
numberOfLines = len(arrayOLines)
#zeros函数 例:zeros((3,4)),创建3行4列以0填充的矩阵
#创建以0填充的Numpy 矩阵
returnMat = zeros((numberOfLines,3))
classLabelVector = []
index = 0
for line in arrayOLines:
#strip()函数 s.strip(rm) 删除s字符串中开头、结尾处,位于 rm删除序列的字符
#当rm为空时,默认删除空白符(包括'\n', '\r', '\t', ' ')
line = line.strip() # 截取所有的回车符
#split():拆分字符串。通过指定分隔符对字符串进行切片,
#并返回分割后的字符串列表(list)
listFromLine = line.split('\t') #解析文件数据到列表
returnMat[index,:] = listFromLine[0:3]
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat,classLabelVector测试解析函数文件 file2matrix( )
#测试
datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
print(" datingDataMat \n " , datingDataMat," \n")
print(" datingLabels \n" , datingLabels[0:20])图3.4 示例1-准备数据
在 .py文件开头导入包
import matplotlib
import matplotlib.pyplot as pltfig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:,1], datingDataMat[:,2])
plt.show() 如图3.5所示,散点图使用datingDataMat矩阵的第二、三列数据,分别表示特征值“玩视频游戏所耗时间比”
图3.5 创建散点图
方程中数字差值最大的属性对计算结果的影响最大,但这三种特征是同等重要的,因此作为三个等权重的特征之一,飞行常客里程数不应该如此严重地影响到计算结果。处理这种不同取值范围的特征时,我们采用的方法是将数值归一化,如将取值范围处理为 0 到 1 或者 -1 到 1 之间。下面公式可以将任意取值范围的特征值转化为 0 到 1 区间内的值:
其中
归一化特征值函数代码:
#该函数可以将数字特征值转化为0到1的区间
def autoNorm(dataSet):
#a.min()返回的就是a中所有元素的最小值
#a.min(0)返回的就是a的每列最小值
#a.min(1)返回的是a的每行最小值
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
#生成一个和数据集相同大小的矩阵
normDataSet = zeros(shape(dataSet))
#获取数据集行数
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m,1))
#特征值相除
normDataSet = normDataSet/tile(ranges, (m,1))
return normDataSet, ranges, minVals
#测试函数
normMat, ranges, minVals = autoNorm(datingDataMat)
print("normMat: \n", normMat,"\n ")
print("ranges: \n", ranges," \n ")
print("minVals: \n", minVals)测试结果,如图3.6所示。
图3.6 测试结果
测试代码:
#测试分类器的效果函数
def datingClassTest():
hoRatio = 0.10
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
#获取数据集的行数
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
# "\" 换行符
classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],\
datingLabels[numTestVecs:m], 20)
print("the classsifier came back with: %d, the real answer is: %d"\
%(classifierResult,datingLabels[i]))
if(classifierResult != datingLabels[i]): errorCount +=1.0
print("the total error rate is:%f" % (errorCount/float(numTestVecs)))
datingClassTest() #测试分类器的正确率 测试算法 测试结果,如图3.7所示。
图3.7 测试结果错误率
分类器处理约会数据集的错误率是 6% 。
约会网站预测函数代码:
#使用算法
def classifyPerson():
resultList = ['not at all', 'in small doses', 'in large doses']
# \ 为换行符
percentTats = float(input(\
"percentage of time spent playing video games?"))
ffMiles = float(input("frequent flier miles earned per year?"))
iceCream = float(input ("liters of ice creamm consumed per year?"))
datingDataMat, datingLabels = file2matrix('datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
inArr = array([ffMiles, percentTats, iceCream])
classifierResult = classify0((inArr-\
minVals)/ranges, normMat, datingLabels, 3)
print("You will probably like this person: ",\
resultList[classifierResult - 1])
classifyPerson() 测试结果,如图3.8所示。
图3.8 约会网站预测结果
示例B:手写字识别系统
(1) 收集数据:提供文本文件。
(2) 准备数据:编写函数img2vector(),将图像格式转化为分类器使用的向量格式。
(3) 分析数据:在python命令行中检查数据,确保它符合要求。
(4) 训练算法:此步骤不适用于K-近邻算法。
(5) 测试算法:编写函数使用提供的部分数据集作为测试样本。 测试样本和非测试样本的区别在于:测试样本是已经完成分类的数据,如果预测分类与实际类别不同,则标记为一个错误。
(6) 使用算法:本列没有此步骤,若你感兴趣你可以用此算法去完成 kaggle 上的 Digital Recognition(数字识别)题目。
转化函数代码:
"""
手写数据集 准备数据:将图像转换为测试向量
"""
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0, 32*i+j] = int(lineStr[j])
#返回数组
return returnVect
#测试函数
testVector = img2vector('testDigits/0_13.txt')
print(testVector[0,0:22])执行结果,如图3.9所示。
图3.9 手写数据集 准备数据
测试结果,如图3.10所示。
图3.10 测试识别手写数字结果
错误率为 1.2% 。
1.k近邻法是基本且简单的分类与回归方法。k近邻法的基本做法是:对给定的训练实例点和输入实例点,首先确定输入实例点的k个最近邻训练实例点,然后利用这k个训练实例点的类的多数来预测输入实例点的类。
2.k近邻模型对应于基于训练数据集对特征空间的一个划分。k近邻法中,当训练集、距离度量、k值及分类决策规则确定后,其结果唯一确定。
3.k近邻法三要素:距离度量、k值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。k值小时,k近邻模型更复杂;k值大时,k近邻模型更简单。k值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的k。常用的分类决策规则是多数表决,对应于经验风险最小化。
[1] Cover T,Hart P. Nearest neighbor pattern classification. IEEE Transactions on Information Theory,1967
[2] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: Data Mining,Inference,and Prediction,2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[3] Friedman J. Flexible metric nearest neighbor classification. Technical Report,1994
[4] Weinberger KQ,Blitzer J,Saul LK. Distance metric learning for large margin nearest neighbor classification. In: Proceedings of the NIPS. 2005
[5] Samet H. The Design and Analysis of Spatial Data Structures. Reading,MA: Addison- Wesley,1990
[6] 统计学习方法/李航著. --北京:清华大学出版社, 2012.3. ISBN 978-7-302-27595-4