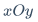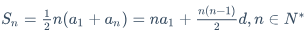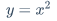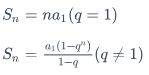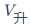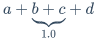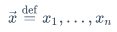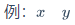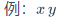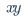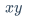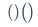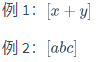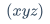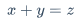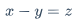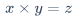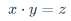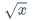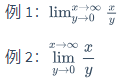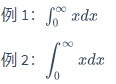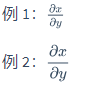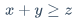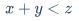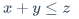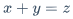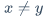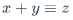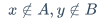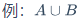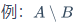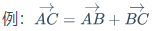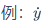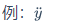Typora_使用_Markdown_嵌入_LaTeX_数学公式符号语法.md

Typora 使用 Markdown 嵌入 LaTeX 数学公式符号语法

博客园不支持渲染 LaTeX 数学公式，需要用到什么公式，请复制到您所用的支持 LaTeX 的编辑器中查看实现效果。Typora 可以渲染 LaTeX 数学公式。

公式内换行

在网上看了许多关于latex多行公式对齐的教程，大多比较凌乱。在此总结一种最整洁的写法：

\begin{eqnarray}    \label{eq}
E&=&(a+b)(a-b)+b^2  \nonumber    
~&=&a^2-b^2+b^2 \nonumber    
~&=&a^2
\end{eqnarray}

以上公式中， “&=&”代表在“=”处对齐， “nonumber”代表此行不参与自动编号，“”表示换行。“～”输入或不输入对结果没有影响。效果如下

有时候公式太长，用=号对齐很难看(有的公式左边很长，右边很短)，此时难免需要进行"公式左对齐"。所需要的环境还是"align"(或者是align*，不带公式编号)。

\begin{align*}\label{2}
  & X(0) = x(0)W_{N}^{0\cdot0} + x(1)W_{N}^{0\cdot1} + \cdots + x(N-1)W_{N}^{0\cdot(N-1)}\\
  & X(1) = x(0)W_{N}^{1\cdot0} + x(1)W_{N}^{1\cdot1} + \cdots + x(N-1)W_{N}^{1\cdot(N-1)} \\
  & \cdots \\
  & X(N-1) = x(0)W_{N}^{(N-1)\cdot0} + x(1)W_{N}^{(N-1)\cdot1} + \cdots + x(N-1)W_{N}^{(N-1)\cdot(N-1)} \\
\end{align*}

$$ \begin{align*}\label{2} & X(0) = x(0)W_{N}^{0\cdot0} + x(1)W_{N}^{0\cdot1} + \cdots + x(N-1)W_{N}^{0\cdot(N-1)}\\ & X(1) = x(0)W_{N}^{1\cdot0} + x(1)W_{N}^{1\cdot1} + \cdots + x(N-1)W_{N}^{1\cdot(N-1)} \\ & \cdots \\ & X(N-1) = x(0)W_{N}^{(N-1)\cdot0} + x(1)W_{N}^{(N-1)\cdot1} + \cdots + x(N-1)W_{N}^{(N-1)\cdot(N-1)} \\ \end{align*} $$

说明1：&符号就是"对齐的位置"，放置在最左边就是多行公式左对齐； 说明2：\符号是每一行公式结束后的换行。

行内与独行

行内公式

将公式插入到本行内

$公式内容$
\inline

例：坐标轴

$xOy$

独行公式

公式单独占用一行

$$公式内容$$
\displaystyle

例：等差数列求和公式：

$$S_n = \frac{1}{2}n(a_1 + a_n) = na_1 + \frac{n(n-1)}{2}d, n\in N^*$$

---

上标、下标与组合

上标

$底数^指数$
$y = x^2$

例：

$y=x^2$

下标

$CuSO_4·5H_2O$

例：

$CuSO_4·5H_2O$

上下标组合

例：等比数列求和公式：

$$S_n = na_1 (q=1)$$
$$S_n = \frac{a_1 (1 - q^n)}{1-q} (q\neq1)$$

---

汉字、字体与格式

汉字形式

\mbox{}

例：

$V_{\mbox{升}}$

字体控制

不加此内容，公式会缩至与文字同高。加此内容，公式会以原大小显示。

\displaystyle

$\displaystyle \frac{x+y}{y+z}$
$\frac{x+y}{y+z}$

下划线符号

\underline

$\underline{x+y}$

标签

\tag{数字}

$\tag{69}$

上大括号

\overbrace{算式}

例：

$\overbrace{a+b+c}^{2.0}$

下大括号

\underbrace{算式}

例：

$a+\underbrace{b+c}_{1.0}+d$

上位符号

\stackrel{上位符号}{基位符号}

例：

$\vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n}$

---

占位符

两个 quad 空格

\qquad

$x\qquad y$

quad 空格

\quad

$x\quad y$

大空格

\

$x \ y$

中空格

\:

$x \: y$

小空格

\,

$x \, y$

贴紧

\!

例：

$x \! y$

无空格

例：

$xy$

---

界定符与组合

括号

\big(算式\big)

例：

$() \big(\big)$

中括号

[]
\left[ \right]

$[x + y]$
$\left[ abc \right]$

第二种中括号可以跨行，例如矩阵左右两边的中括号

大括号

\{算式\}

例：

$\{x + y\}$

自适应括号

\left(算式 \right)

例：

$\left(xyz\right)$

组合公式

${n+1 \choose k}={n \choose k}+{n \choose k-1}$
$\sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots$

左大括号 联立公式

方法一：

f(x)=\left\{
\begin{aligned}
x & = & \cos(t) \\
y & = & \sin(t) \\
z & = & \frac xy
\end{aligned}
\right.

$$ f(x)=\left{ \begin{aligned} x & = & \cos(t) \\ y & = & \sin(t) \\ z & = & \frac xy \end{aligned} \right. $$

方法二：

$$ F^{HLLC}=\left{ \begin{array}{rcl} F_L & & {0 < S_L}\ F^_L & & {S_L \leq 0 < S_M}\ F^_R & & {S_M \leq 0 < S_R}\ F_R & & {S_R \leq 0} \end{array} \right. $$

 F^{HLLC}=\left\{
\begin{array}{rcl}
F_L   &   & {0   <   S_L}\\
F^*_L  &   & {S_L \leq 0 < S_M}\\
F^*_R  &   & {S_M \leq 0 < S_R}\\
F_R   &   & {S_R \leq 0}
\end{array} \right. 

方法三:

$$f(x)= \begin{cases} 0& \text{x=0}\\ 1& \text{x!=0} \end{cases}$$

f(x)=
\begin{cases}
0& \text{x=0}\\
1& \text{x!=0}
\end{cases}

---

四则运算

加

例：

$x+y=z$

减

例：

$x-y=z$

加减运算

\pm

例：

$x \pm y = z$

减加运算

\mp

例：

$x \mp y = z$

乘

叉乘

\times

例：

$x \times y = z$

点乘

\cdot

例：

$x \cdot y = z$

星乘

\ast

例：

$x \ast y = z$

除

除号

\div

例：

$x \div y = z$

斜杠除

x/y

例：

$x / y = z$

分式

\frac{分子}{分母}
{分子}\over{分母}

$\frac{x+y}{y+z}$
${x+y}\over{y+z}$

绝对值

|算式|

例：

$y = |x|$

---

高级运算

平均数

\overline{算式}

例：

$\overline{xyz}$

开方

开平方

\sqrt

例：

$\sqrt x$

开多次方

\sqrt[开方数]{被开方数}

例：

$\sqrt[3]{x+y}$

对数

\log

例：

$\log_5{x}$

极限

\lim
\displaystyle \lim

$\lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$
$\displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}}$

$\lim^{x \to \infty}{y \to 0}{\frac{x}{y}}$ $\displaystyle \lim^{x \to \infty}{y \to 0}{\frac{x}{y}}$

求和

\sum
\displaystyle \sum

$\sum^{x \to -\infty}_{y \to 0}{\frac{x}{y}}$
$\displaystyle \sum^{x \to -\infty}_{y \to 0}{\frac{x}{y}}$

$\sum^{x \to -\infty}{y \to 0}{\frac{x}{y}}$ $\displaystyle \sum^{x \to -\infty}{y \to 0}{\frac{x}{y}}$

积分

\int
\displaystyle \int

$\int^{\infty}_{0}{xdx}$
$\displaystyle \int^{\infty}_{0}{xdx}$

$\int^{\infty}{0}{xdx}$ $\displaystyle \int^{\infty}{0}{xdx}$

微分

\partial
\displaystyle \partial

$\frac{\partial x}{\partial y}$
$\displaystyle \frac{\partial x}{\partial y}$

$\frac{\partial x}{\partial y}$ $\displaystyle \frac{\partial x}{\partial y}$

矩阵

\begin{matrix} \end{matrix}

例：

$$\left[ \begin{matrix} 1 & 2  & \cdots & 5 & 6 & \cdots & 9 & 10 \\ \vdots & \vdots & \cdots & \vdots & \vdots & \cdots & \cdots & \ddots \\ a & b & \cdots & e & f & \cdots & i & j \end{matrix} \right]$$

$$\left[ \begin{matrix} 1 & 2 & \cdots & 5 & 6 & \cdots & 9 & 10 \ \vdots & \vdots & \cdots & \vdots & \vdots & \cdots & \cdots & \ddots \ a & b & \cdots & e & f & \cdots & i & j \end{matrix} \right]$$

逻辑运算

大于、小于和等于

大于

例：

$x+y>z$

大于等于

\geq

例：

$x+y \geq z$

小于

例：

$x+y<z$

小于等于

\leq

例：

$x+y \leq z$

等于

例：

$x+y=z$

不等于

\neq

例：

$x \neq y$

不大于等于、不小于等于

不大于等于

\ngeq
\not\geq

$x \ngeq y$
$x \not\geq y$

不小于等于

\nleq
\not\leq

$x \nleq y$
$x \not\leq y$

约等于

\approx

$\frac{1}{3} \approx 0.3$
$\displaystyle \frac{1}{3} \approx 0.3$

$\frac{1}{3} \approx 0.3$ $\displaystyle \frac{1}{3} \approx 0.3$

恒等于

\equiv

例：

$x + y \equiv z$

---

集合运算

属于、不属于

属于

\in

例：

$x \in A$

不属于

\notin
\not\in

例：

$x \notin A, y \not \in B$

子集运算

子集

\subset
\supset

$A \subset B$
$A \supset B$

非子集

\not\subset
\not\supset

$A \not\subset B$
$A \not\supset B$

真子集

\subseteq
\supseteq

$A \subseteq B$
$A \supseteq B$

非真子集

\subsetneq
\supsetneq

$A \subsetneq B$
$A \supsetneq B$

集合布尔运算

交集

\cap

$A \cap B$

并集

\cup

$A \cup B$

差集

\setminus

$A \setminus B$

同或运算

\bigodot

$A \bigodot B$

同与运算

\bigotimes

$A \bigotimes B$

常用数集

\mathbb{数集字母}

空集

\empty
\emptyset

---

数学符号

无穷

\infty

虚数

\imath
\jmath

向量符号

\vec{字母}

$\vec{AC} = \vec{AB} + \vec{BC}$

$\vec{AC} = \vec{AB} + \vec{BC}$

导数

一阶导数

$$\dot{a}$$

\dot{a}

二阶导数

$$\ddot{a}$$

\ddot{a}

以此类推：

箭头

上箭头

\uparrow

双线上箭头

\Uparrow

下箭头

\downarrow

双线下箭头

\Downarrow

左箭头

\leftarrow

双线左箭头

\Leftarrow

右箭头

\rightarrow

双线右箭头

\Rightarrow

箭头上文字

$\stackrel{a}{\longrightarrow}$

示例：

$0\stackrel{a}{\longrightarrow}1$

更多箭头符号

latex 显示效果

\uparrow    ↑
\downarrow    ↓
\Uparrow    ⇑
\Downarrow    ⇓
\updownarrow    ↕
\Updownarrow    ⇕
\rightarrow    →
\leftarrow    ←
\Rightarrow    ⇒
\Leftarrow    ⇐
\leftrightarrow    ↔
\Leftrightarrow    ⇔
\longrightarrow    ⟶
\longleftarrow    ⟵
\Longrightarrow    ⟹
\Longleftarrow    ⟸
\longleftrightarrow    ⟷
\Longleftrightarrow    ⟺

latex    显示效果
\mapsto    ↦
\longmapsto    ⟼
\hookleftarrow    ↩
\hookrightarrow    ↪
\leftharpoonup    ↼
\rightharpoonup    ⇀
\leftharpoondown    ↽
\rightharpoondown    ⇁
\rightleftharpoons    ⇌
\leadsto    ⇝
\nearrow    ↗
\searrow    ↘
\swarrow    ↙
\nwarrow    ↖
\nleftarrow    ↚
\nrightarrow    ↛
\nLeftarrow    ⇍
\nRightarrow    ⇏
\nleftrightarrow    ↮
\nLeftrightarrow    ⇎
\dashrightarrow    ⇢
\dashleftarrow    ⇠
\leftleftarrows    ⇇
\leftrightarrows    ⇆
\Lleftarrow    ⇚
\twoheadleftarrow    ↞
\leftarrowtail    ↢
\looparrowleft    ↫
\leftrightharpoons    ⇋
\curvearrowleft    ↶
\circlearrowleft    ↺
\Lsh    ↰
\upuparrows    ⇈
\upharpoonleft    ↿
\downharpoonleft    ⇃
\multimap    ⊸
\leftrightsquigarrow    ↭
\rightrightarrows    ⇉
\rightleftarrows    ⇄
\rightrightarrows    ⇉
\rightleftarrows    ⇄
\twoheadrightarrow    ↠
\rightarrowtail    ↣
\looparrowright    ↬
\rightleftharpoons    ⇌
\curvearrowright    ↷
\circlearrowright    ↻
\Rsh    ↱
\downdownarrows    ⇊
\upharpoonright    ↾
\downharpoonright    ⇂
\rightsquigarrow    ⇝

---

省略号

低端对齐

\ldots

中线对齐

\cdots

垂直对齐

\vdots

斜对齐

\ddots

其他数学符号 音节符号

ā

$\bar{a}$

á

$\acute{a}$

ǎ

$\check{a}$

à

$\grave{a}$

â

$\hat{a}$

$\breve{a}$

$\breve{a}$

ã

$\tilde{a}$

å

$\mathring{x}$

$\mathring{x}$

希腊字母

大写字母	效果	实现	小写字母	效果	实现
A	$\Alpha$	\Alpha	α	$\alpha$	\alpha
B	$\Beta$	\Beta	β	$\beta$	\beta
Γ	$\Gamma$	\Gamma	γ	$\gamma$	\gamma
Δ	$\Delta$	\Delta	δ	$\delta$	\delta
Ε	$\Epsilon$	\Epsilon	ε	$\epsilon$	\epsilon
Ζ	$\Zeta$	\Zeta	ζ	$\zeta$	\zeta
Η	$\Eta$	\Eta	η	$\eta$	\eta
Θ	$\Theta$	\Theta	θ	$\theta$	\theta
Ι	$\Iota$	\Iota	ι	$\iota$	\iota
Κ	$\Kappa$	\Kappa	κ	$\kappa$	\kappa
Λ	$\Lambda$	\Lambda	λ	$\lambda$	\lambda
Μ	$\Mu$	\Mu	μ	$\mu$	\mu
Ν	$\Nu$	\Nu	ν	$\nu$	\nu
Ξ	$\Xi$	\Xi	ξ	$\xi$	\xi
Ο	$\Omicron$	\Omicron	ο	$\omicron$	\omicron
Π	$\Pi $	\Pi	π	$\pi$	\pi
Ρ	$\Rho$	\Rho	ρ	$\rho$	\rho
Σ	$\Sigma$	\Sigma	σ	$\sigma$	\sigma
Τ	$\Tau$	\Tau	τ	$\tau$	\tau
Υ	$\Upsilon$	\Upsilon	υ	$\upsilon$	\upsilon
Φ	$\Phi$	\Phi	φ	$\phi$	\phi
Χ	$\Chi$	\Chi	χ	$\chi$	\chi
Ψ	$\Psi$	\Psi	ψ	$\psi$	\psi
Ω	$\Omega$	\Omega	ω	$\omega$	\omega

• 此文参考自 @Daniel_Gavin 的文章《Markdown数学公式语法》（ 简书 ）
• 推荐网站：Online LaTeX Equation Editor

分类: Markdown_LaTeX

$$ f(x)=\left{ \begin{aligned} x & = & \cos(t) \\ y & = & \sin(t) \\ z & = & \frac xy \end{aligned} \right. $$

$$ \displaystyle \lim^{x \to \infty}_{y \to 0}{\frac{x}{y}} $$

$$ \vec{x}\stackrel{\mathrm{def}}{=}{x_1,\dots,x_n} $$

$$ \left[ \begin{matrix} 1 & 2 & \cdots & 5 & 6 & \cdots & 9 & 10 \ \vdots & \vdots & \cdots & \vdots & \vdots & \cdots & \cdots & \ddots \ a & b & \cdots & e & f & \cdots & i & j \end{matrix} \right] $$

$$ {n+1 \choose k}={n \choose k}+{n \choose k-1} $$

$$ \sum_{k_0,k_1,\ldots>0 \atop k_0+k_1+\cdots=n}A_{k_0}A_{k_1}\cdots $$

$$ \begin {align*}\label{3} & X(0) = x(0)W_{N}^{0\cdot0} + x(1)W_{N}^{0\cdot1} + \cdots + x(N-1)W_{N}^{0\cdot(N-1)}\\ & X(1) = x(0)W_{N}^{1\cdot0} + x(1)W_{N}^{1\cdot1} + \cdots + x(N-1)W_{N}^{1\cdot(N-1)} \\ & \cdots \\ & X(N-1) = x(0)W_{N}^{(N-1)\cdot0} + x(1)W_{N}^{(N-1)\cdot1} + \cdots + x(N-1)W_{N}^{(N-1)\cdot(N-1)} \\ \end{align*} $$