参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

如果不对递归有深刻的理解，本题有点难单纯移除一个节点那还不够，要修剪！

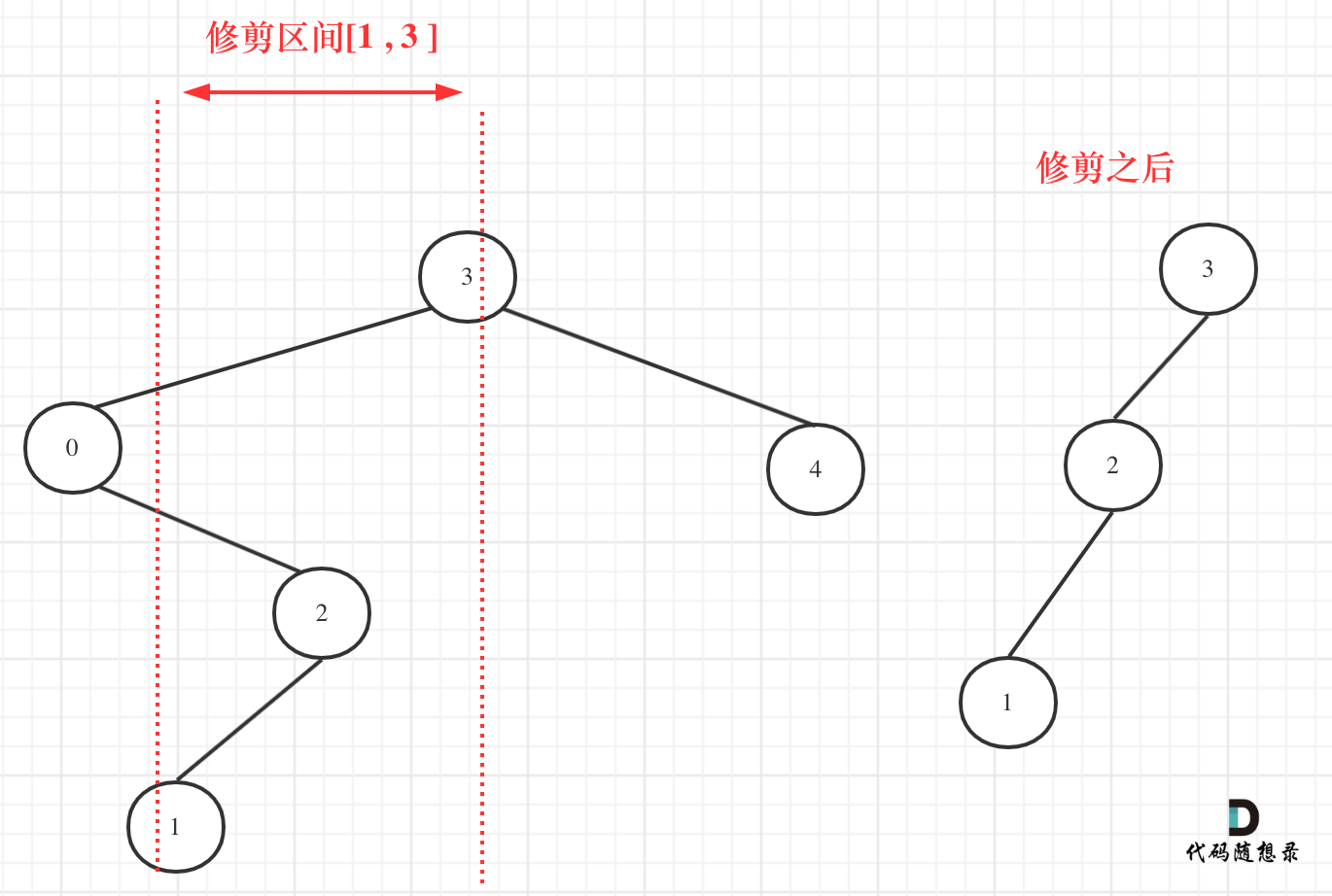
669. 修剪二叉搜索树

力扣题目链接

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

算法公开课

《代码随想录》算法视频公开课：你修剪的方式不对，我来给你纠正一下！| LeetCode：669. 修剪二叉搜索树，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

相信看到这道题目大家都感觉是一道简单题（事实上leetcode上也标明是简单）。

但还真的不简单！

递归法

直接想法就是：递归处理，然后遇到 root->val < low || root->val > high 的时候直接return NULL，一波修改，赶紧利落。

不难写出如下代码：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr || root->val < low || root->val > high) return nullptr;
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的，还要考虑节点0的右子树。

我们在重新关注一下第二个示例，如图：

所以以上的代码是不可行的！

从图中可以看出需要重构二叉树，想想是不是本题就有点复杂了。

其实不用重构那么复杂。

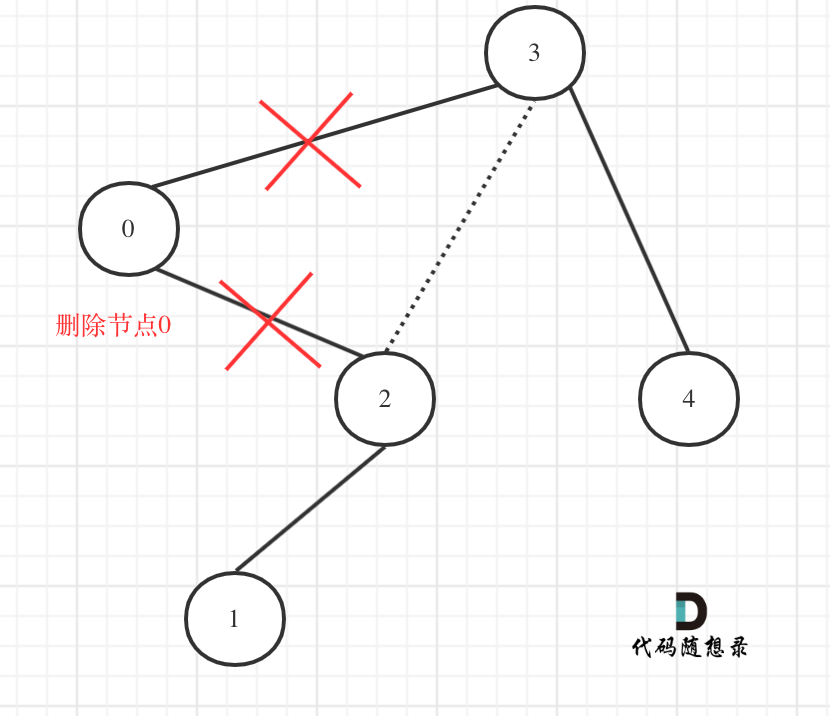
在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子节点2 直接赋给节点3的左孩子就可以了（就是把节点0从二叉树中移除），如图：

理解了最关键部分了我们再递归三部曲：

确定递归函数的参数以及返回值

这里我们为什么需要返回值呢？

因为是要遍历整棵树，做修改，其实不需要返回值也可以，我们也可以完成修剪（其实就是从二叉树中移除节点）的操作。

但是有返回值，更方便，可以通过递归函数的返回值来移除节点。

这样的做法在二叉树：搜索树中的插入操作和二叉树：搜索树中的删除操作中大家已经了解过了。

代码如下：

TreeNode* trimBST(TreeNode* root, int low, int high)

确定终止条件

修剪的操作并不是在终止条件上进行的，所以就是遇到空节点返回就可以了。

if (root == nullptr ) return nullptr;

确定单层递归的逻辑

如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。

代码如下：

if (root->val < low) {
    TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
    return right;
}

如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。

代码如下：

if (root->val > high) {
    TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
    return left;
}

接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。

最后返回root节点，代码如下：

root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;

此时大家是不是还没发现这多余的节点究竟是如何从二叉树中移除的呢？

在回顾一下上面的代码，针对下图中二叉树的情况：

如下代码相当于把节点0的右孩子（节点2）返回给上一层，

if (root->val < low) {
    TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
    return right;
}

然后如下代码相当于用节点3的左孩子把下一层返回的节点0的右孩子（节点2）接住。

root->left = trimBST(root->left, low, high);

此时节点3的左孩子就变成了节点2，将节点0从二叉树中移除了。

最后整体代码如下：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr ) return nullptr;
        if (root->val < low) {
            TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点
            return right;
        }
        if (root->val > high) {
            TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点
            return left;
        }
        root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
        root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
        return root;
    }
};

精简之后代码如下：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr) return nullptr;
        if (root->val < low) return trimBST(root->right, low, high);
        if (root->val > high) return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

只看代码，其实不太好理解节点是如何移除的，这一块大家可以自己再模拟模拟！

迭代法

因为二叉搜索树的有序性，不需要使用栈模拟递归的过程。

在剪枝的时候，可以分为三步：

将root移动到[L, R] 范围内，注意是左闭右闭区间
剪枝左子树
剪枝右子树

代码如下：

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int L, int R) {
        if (!root) return nullptr;

        // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while (root != nullptr && (root->val < L || root->val > R)) {
            if (root->val < L) root = root->right; // 小于L往右走
            else root = root->left; // 大于R往左走
        }
        TreeNode *cur = root;
        // 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
        while (cur != nullptr) {
            while (cur->left && cur->left->val < L) {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }
        cur = root;

        // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        while (cur != nullptr) {
            while (cur->right && cur->right->val > R) {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};

总结

修剪二叉搜索树其实并不难，但在递归法中大家可看出我费了很大的功夫来讲解如何删除节点的，这个思路其实是比较绕的。

最终的代码倒是很简洁。

如果不对递归有深刻的理解，这道题目还是有难度的！

本题我依然给出递归法和迭代法，初学者掌握递归就可以了，如果想进一步学习，就把迭代法也写一写。

其他语言版本

Java

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

Python

递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
        '''
        确认递归函数参数以及返回值：返回更新后剪枝后的当前root节点
        '''
        # Base Case
        if not root: return None

        # 单层递归逻辑
        if root.val < low:
            # 若当前root节点小于左界：只考虑其右子树，用于替代更新后的其本身，抛弃其左子树整体
            return self.trimBST(root.right, low, high)
        
        if high < root.val:
            # 若当前root节点大于右界：只考虑其左子树，用于替代更新后的其本身，抛弃其右子树整体
            return self.trimBST(root.left, low, high)

        if low <= root.val <= high:
            root.left = self.trimBST(root.left, low, high)
            root.right = self.trimBST(root.right, low, high)
            # 返回更新后的剪枝过的当前节点root
            return root

Go

// 递归
func trimBST(root *TreeNode, low int, high int) *TreeNode {
    if root == nil {
        return nil
    }
    if root.Val < low {     //如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
        right := trimBST(root.Right, low, high)
        return right
    }
    if root.Val > high {    //如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
        left := trimBST(root.Left, low, high)
        return left
    }
    root.Left = trimBST(root.Left, low, high)
    root.Right = trimBST(root.Right, low, high)
    return root
}

// 迭代
func trimBST(root *TreeNode, low int, high int) *TreeNode {
    if root == nil {
        return nil
    }
    // 处理 root，让 root 移动到[low, high] 范围内，注意是左闭右闭
    for root != nil && (root.Val < low || root.Val > high) {
        if root.Val < low {
            root = root.Right
        } else {
            root = root.Left
        }
    }
    cur := root
    // 此时 root 已经在[low, high] 范围内，处理左孩子元素小于 low 的情况（左节点是一定小于 root.Val，因此天然小于 high）
    for cur != nil {
        for cur.Left != nil && cur.Left.Val < low {
            cur.Left = cur.Left.Right
        }
        cur = cur.Left
    }
    cur = root
    // 此时 root 已经在[low, high] 范围内，处理右孩子大于 high 的情况
    for cur != nil {
        for cur.Right != nil && cur.Right.Val > high {
            cur.Right = cur.Right.Left
        }
        cur = cur.Right
    }
    return root
}

JavaScript版本

迭代：

var trimBST = function(root, low, high) {
   if(root === null) {
       return null;
   }
   while(root !== null && (root.val < low || root.val > high)) {
       if(root.val < low) {
           root = root.right;
       }else {
           root = root.left;
       }
   }
   let cur = root;
   while(cur !== null) {
       while(cur.left && cur.left.val < low) {
           cur.left = cur.left.right;
       }
       cur = cur.left;
   }
   cur =  root;
   //判断右子树大于high的情况
   while(cur !== null) {
       while(cur.right && cur.right.val > high) {
           cur.right = cur.right.left;
       }
       cur = cur.right;
   }
   return root;
};

递归：

var trimBST = function (root,low,high) { 
    if(root === null) {
        return null;
    }
    if(root.val < low) {
        let right = trimBST(root.right, low, high);
        return right;
    }
    if(root.val > high) {
        let left = trimBST(root.left, low, high);
        return left;
    }
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
 }

TypeScript

递归法

function trimBST(root: TreeNode | null, low: number, high: number): TreeNode | null {
    if (root === null) return null;
    if (root.val < low) {
        return trimBST(root.right, low, high);
    }
    if (root.val > high) {
        return trimBST(root.left, low, high);
    }
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
};

迭代法

function trimBST(root: TreeNode | null, low: number, high: number): TreeNode | null {
    while (root !== null && (root.val < low || root.val > high)) {
        if (root.val < low) {
            root = root.right;
        } else if (root.val > high) {
            root = root.left;
        }
    }
    let curNode: TreeNode | null = root;
    while (curNode !== null) {
        while (curNode.left !== null && curNode.left.val < low) {
            curNode.left = curNode.left.right;
        }
        curNode = curNode.left;
    }
    curNode = root;
    while (curNode !== null) {
        while (curNode.right !== null && curNode.right.val > high) {
            curNode.right = curNode.right.left;
        }
        curNode = curNode.right;
    }
    return root;
};

Scala

递归法:

object Solution {
  def trimBST(root: TreeNode, low: Int, high: Int): TreeNode = {
    if (root == null) return null
    if (root.value < low) return trimBST(root.right, low, high)
    if (root.value > high) return trimBST(root.left, low, high)
    root.left = trimBST(root.left, low, high)
    root.right = trimBST(root.right, low, high)
    root
  }
}

rust

// 递归

impl Solution {
    pub fn trim_bst(
        root: Option<Rc<RefCell<TreeNode>>>,
        low: i32,
        high: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        root.as_ref()?;
        let mut node = root.as_ref().unwrap().borrow_mut();
        if node.val < low {
            return Self::trim_bst(node.right.clone(), low, high);
        }
        if node.val > high {
            return Self::trim_bst(node.left.clone(), low, high);
        }

        node.left = Self::trim_bst(node.left.clone(), low, high);
        node.right = Self::trim_bst(node.right.clone(), low, high);
        drop(node);
        root
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

0669.修剪二叉搜索树.md

0669.修剪二叉搜索树.md

669. 修剪二叉搜索树

算法公开课

思路

递归法

迭代法

总结

其他语言版本

Java

Python

Go

JavaScript版本

TypeScript

Scala

rust

Files

0669.修剪二叉搜索树.md

Latest commit

History

0669.修剪二叉搜索树.md

File metadata and controls

669. 修剪二叉搜索树

算法公开课

思路

递归法

迭代法

总结

其他语言版本

Java

Python

Go

JavaScript版本

TypeScript

Scala

rust