Skip to content

Latest commit

 

History

History
284 lines (225 loc) · 6.76 KB

README.md

File metadata and controls

284 lines (225 loc) · 6.76 KB

1135. 最低成本联通所有城市

English Version

题目描述

想象一下你是个城市基建规划者，地图上有 N 座城市，它们按以 1 到 N 的次序编号。

给你一些可连接的选项 conections，其中每个选项 conections[i] = [city1, city2, cost] 表示将城市 city1 和城市 city2 连接所要的成本。（连接是双向的，也就是说城市 city1 和城市 city2 相连也同样意味着城市 city2 和城市 city1 相连）。

返回使得每对城市间都存在将它们连接在一起的连通路径（可能长度为 1 的）最小成本。该最小成本应该是所用全部连接代价的综合。如果根据已知条件无法完成该项任务，则请你返回 -1。

 

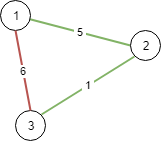
示例 1：

输入：N = 3, conections = [[1,2,5],[1,3,6],[2,3,1]]
输出：6
解释：
选出任意 2 条边都可以连接所有城市，我们从中选取成本最小的 2 条。

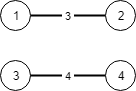
示例 2：

输入：N = 4, conections = [[1,2,3],[3,4,4]]
输出：-1
解释： 
即使连通所有的边，也无法连接所有城市。

 

提示：

  1. 1 <= N <= 10000
  2. 1 <= conections.length <= 10000
  3. 1 <= conections[i][0], conections[i][1] <= N
  4. 0 <= conections[i][2] <= 10^5
  5. conections[i][0] != conections[i][1]

解法

最小生成树 + 并查集。

并查集模板：

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

Python3

class Solution:
    def minimumCost(self, n: int, connections: List[List[int]]) -> int:
        p = list(range(n))
        connections.sort(key=lambda x: x[2])
        res = 0

        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        def union(a, b):
            pa, pb = find(a - 1), find(b - 1)
            if pa == pb:
                return False
            p[pa] = pb
            return True

        for c1, c2, cost in connections:
            if union(c1, c2):
                n -= 1
                res += cost
                if n == 1:
                    return res
        return -1

Java

class Solution {
    private int[] p;

    public int minimumCost(int n, int[][] connections) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        Arrays.sort(connections, (a, b) -> a[2] - b[2]);
        int res = 0;
        for (int[] e : connections) {
            if (union(e[0], e[1])) {
                res += e[2];
                --n;
                if (n == 1) {
                    return res;
                }
            }
        }
        return -1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    private boolean union(int a, int b) {
        int pa = find(a - 1), pb = find(b - 1);
        if (pa == pb) {
            return false;
        }
        p[pa] = pb;
        return true;
    }
}

C++

class Solution {
public:
    vector<int> p;

    int minimumCost(int n, vector<vector<int>> &connections) {
        p.resize(n);
        for (int i = 0; i < n; ++i) p[i] = i;
        auto cmp = [](auto &a, auto &b)
        {
            return a[2] < b[2];
        };
        sort(connections.begin(), connections.end(), cmp);
        int res = 0;
        for (auto e : connections)
        {
            if (unite(e[0], e[1]))
            {
                res += e[2];
                --n;
                if (n == 1) return res;
            }
        }
        return -1;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    bool unite(int a, int b) {
        int pa = find(a - 1), pb = find(b - 1);
        if (pa == pb) return false;
        p[pa] = pb;
        return true;
    }
};

Go

var p []int

func minimumCost(n int, connections [][]int) int {
	p = make([]int, n)
	for i := 0; i < len(p); i++ {
		p[i] = i
	}
	sort.Slice(connections, func(i, j int) bool {
		return connections[i][2] < connections[j][2]
	})
	res := 0
	for _, e := range connections {
		if union(e[0], e[1]) {
			res += e[2]
			n--
			if n == 1 {
				return res
			}
		}
	}
	return -1
}

func find(x int) int {
	if p[x] != x {
		p[x] = find(p[x])
	}
	return p[x]
}

func union(a, b int) bool {
	pa, pb := find(a-1), find(b-1)
	if pa == pb {
		return false
	}
	p[pa] = pb
	return true
}

...