README.md

1572. 矩阵对角线元素的和

English Version

题目描述

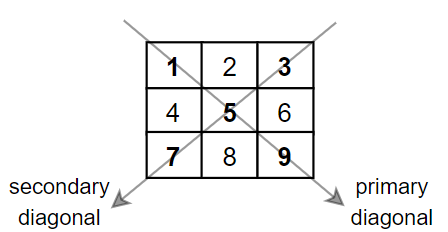
给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

 

示例  1：

输入：mat = [[1,2,3],
            [4,5,6],
            [7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例  2：

输入：mat = [[1,1,1,1],
            [1,1,1,1],
            [1,1,1,1],
            [1,1,1,1]]
输出：8

示例 3：

输入：mat = [[5]]
输出：5

 

提示：

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

解法

Python3

class Solution:
    def diagonalSum(self, mat: List[List[int]]) -> int:
        n = len(mat)
        res = 0
        for i in range(n):
            res += mat[i][i] + (0 if n - i - 1 == i else mat[i][n - i - 1])
        return res

Java

class Solution {
    public int diagonalSum(int[][] mat) {
        int n = mat.length;
        int res = 0;
        for (int i = 0; i < n; ++i) {
            res += mat[i][i] + (n - i - 1 == i ? 0 : mat[i][n - i - 1]);
        }
        return res;
    }
}

TypeScript

function diagonalSum(mat: number[][]): number {
    let n = mat.length;
    let ans = 0;
    for (let i = 0; i < n; i++) {
        ans += mat[i][i];
        let j = n - 1 - i;
        if (i != j) {
            ans += mat[i][j];
        }
    }
    return ans;
};

C++

class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int n = mat.size();
        int res = 0;
        for (int i = 0; i < n; ++i) {
            res += mat[i][i] + (n - i - 1 == i ? 0 : mat[i][n - i - 1]);
        }
        return res;
    }
};

Go

func diagonalSum(mat [][]int) int {
	n, res := len(mat), 0
	for i := 0; i < n; i++ {
		res += mat[i][i]
		if n-i-1 != i {
			res += mat[i][n-i-1]
		}
	}
	return res
}

...