README.md

1886. 判断矩阵经轮转后是否一致

English Version

题目描述

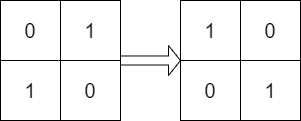
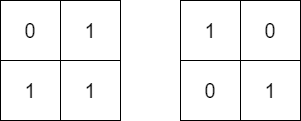
给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素 若干次 ，如果能够使 mat 与 target 一致，返回 true ；否则，返回 false 。

 

示例 1：

输入：mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
输出：true
解释：顺时针轮转 90 度一次可以使 mat 和 target 一致。

示例 2：

输入：mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
输出：false
解释：无法通过轮转矩阵中的元素使 equal 与 target 一致。

示例 3：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
输出：true
解释：顺时针轮转 90 度两次可以使 mat 和 target 一致。

 

提示：

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] 和 target[i][j] 不是 0 就是 1

解法

旋转矩阵，判断矩阵是否一致。

Python3

class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        def rotate(matrix):
            n = len(matrix)
            for i in range(n // 2):
                for j in range(i, n - 1 - i):
                    t = matrix[i][j]
                    matrix[i][j] = matrix[n - j - 1][i]
                    matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
                    matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
                    matrix[j][n - i - 1] = t
        for _ in range(4):
            if mat == target:
                return True
            rotate(mat)
        return False

Java

class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int times = 4;
        while (times-- > 0) {
            if (equals(mat, target)) {
                return true;
            }
            rotate(mat);
        }
        return false;
    }
    
    private void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = i; j < n - 1 - i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = t;
            }
        }
    }
    
    private boolean equals(int[][] nums1, int[][] nums2) {
        int n = nums1.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (nums1[i][j] != nums2[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}

...