Skip to content

Latest commit

 

History

History
125 lines (98 loc) · 9.17 KB

PCA.md

File metadata and controls

125 lines (98 loc) · 9.17 KB

Principal Component Analysis and Singular Value Decomposition

Singular Value Decomposition

Singular value decomposition is an extension of eigenvector decomposition of a matrix.

For the square matrix $M_{n\times n}$, we can compute the eigenvalues and eigenvectors: $$M_{n\times n}v=\lambda v$$ where the eigenvector $v\in \mathbb{R}^n$, the eigenvalue $\lambda \in\mathbb{R}$. It is equivalent to solve the linear equation system $(M_{n\times n}-\lambda I_{n\times n})v=0$ where $I_{n\times n}$ is the $n$th order identity matrix. Especially, when $M_{n\times n}$ is symmetrical i.e. $M^T=M$, what are the properties of eigenvalue and eigenvector?

Theorem: All eigenvalues of a symmetrical matrix are real.

Proof: Let $A$ be a real symmetrical matrix and $Av=\lambda v$. We want to show the eigenvalue $\lambda$ is real. Let $v^{\star}$ be conjugate transpose of $v$. $v^{\star}Av=\lambda v^{\star}v,(1)$. If $Av=\lambda v$，thus $(Av)^{\star}=(\lambda v)^{\star}$, i.e. $v^{\star}A=\bar{\lambda}v^{\star}$. We can infer that $v^{\star}Av=\bar{\lambda}v^{\star}v,(2)$.By comparing the equation (1) and (2), we can obtain that $\lambda=\bar{\lambda}$ where $\bar{\lambda}$ is the conjugate of $\lambda$.

Theorem: Every symmetrical matrix can be diagonalized.

See more at http://mathworld.wolfram.com/MatrixDiagonalization.html.

When the matrix is rectangle i.e. the number of columns and the number of rows are not equal, what is the counterpart of eigenvalues and eigenvectors? Another question is if every matrix $M_{m\times n}\in\mathbb{R}^{m\times n}$ can be written as the sum of rank-1 matrix and how? $$M_{m\times n}=\sum_{i}^{r}p_i q_i=P_{m\times r}Q_{r\times n}$$ where $p_i\in\mathbb{R}^m$,$q_i\in\mathbb{R}^n$ and $r$ is integer.

They are from the square matrices $M_{m\times n}^TM_{m\times n}=A_{n\times n}$ and $M_{m\times n}M_{m\times n}^T=B_{m\times m}$. It is obvious that the matrix $A$ and $B$ are symmetrical.

Theorem: The matrix $A$ and $B$ has the same eigenvalues except zeroes.

Proof: We know that $A=M_{m\times n}^TM_{m\times n}$ and $B=M_{m\times n}M_{m\times n}^T$. Let $Av=\lambda v$ i.e. $M_{m\times n}^TM_{m\times n} v=\lambda v$, which can be rewritten as $M_{m\times n}^T(M_{m\times n} v)=\lambda v,(1)$, where $v\in\mathbb{R}^n$. We multiply the matrix $M_{m\times n}$ in the left of both sides of equation (1), then we obtain $M_{m\times n}M_{m\times n}^T(M_{m\times n} v)=M_{m\times n}(\lambda v)=\lambda(M_{m\times n} v)$ such that $B(M_{m\times n}v)=\lambda M_{m\times n}v$.

Another observation of $A$ and $B$ is that the trace of $A$ is equal to the trace of $B$, i.e. $tr(A)=tr(M_{m\times n}^TM_{m\times n})=tr(B)=tr(M_{m\times n}M_{m\times n}^T)=\sum_{i,j}m_{ij}^2$ where $m_{ij}$ is the element of matrix $M_{m\times n}$.

Theorem: The matrix $A$ and $B$ are non-negative definite, i.e. $\left<v,Av\right>\geq 0, \forall v\in\mathbb{R}^n$ and $\left<u,Bu\right>\geq 0, \forall u\in\mathbb{R}^m$.

Proof: It is $\left<v,Av\right>=\left<v,M_{m\times n}^TM_{m\times n}v\right>=(Mv)^T(Mv)=|Mv|_2^2\geq 0$ as well as $B$.

We can infer that the eigenvalues of matrix $A$ and $B$ are nonnegative. We ca prove it by counterproof. Suppose that $\lambda < 0$ and $Av = \lambda v$, we can conclude that $\left<v,Av\right>=\left<v,\lambda v\right>=(Mv)^T(Mv)=|Mv|_2^2 = \lambda {|v|}_2^2\geq 0$ while $v =\not \vec{0}$ and $\lambda < 0$. The contradiction occurs.

The eigenvalues of $A$ or $B$ really matters. And it is possible to compute the eigenvalues and eigenvectors of $A_{n\times n}$ or $B_{m\times m}$. For example, we assume that $A_{n\times n}=V_{n\times n}\Lambda V_{n\times n}^{T}$, where the diagonal matrix $\Lambda = Diag(\lambda_1,\dots, \lambda_n)$ consists of eigenvalues, the orthogonal matrix $V_{n\times n}=(v_1,\dots, v_n)$ consists of eigenvectors ${v_1,\dots, v_n}\subset \mathbb{R}^{n}$ so that $A_{n\times n}v_i = \lambda_i v_i$ for $i=1,2,\dots, n$. In anther word, $M_{m\times n}^TM_{m\times n} v_i = \lambda_i v_i$ or ${v_i}^{T} M_{m\times n}^TM_{m\times n}= \lambda_i {v_i}^{T}\Rightarrow(M_{m\times n}v_i)^{T}M_{m\times n}=\lambda_i {v_i}^{T}$. The vector $M_{m\times n}v_i\in\mathbb{R}^{m}$ for $i=1, 2, \dots, n$ can make up a matrix and $\left<M_{m\times n}v_i, M_{m\times n}v_j\right>=(M_{m\times n}v_i)^{T}M_{m\times n}v_j=0$ if $i =\not j$ because of the fact that $M_{m\times n}v_i$ is the eigenvector of $B = M_{m\times n}M_{m\times n}^{T}$. What is more, we have that $(M_{m\times n}\Lambda)^{T}M_{m\times n}=\Lambda V_{n\times n}^{T}$.

It is known that $\sum_{i=1}^{n}\lambda_i=tr(A)$. Note thta the columns of $M_{m\times n}\Lambda$ are perpendicular to each other.

Theorem: $M_{m\times n}=U_{m\times m}\Sigma_{m\times n} V_{n\times n}^T$, where

  • $U_{m\times m}$ is an $m \times m$ orthogonal matrix;
  • $\Sigma_{m\times n}$ is a diagonal $m \times n$ matrix with non-negative real numbers on the diagonal,
  • $V_{n\times n}^T$ is the transpose of an $n \times n$ orthogonal matrix.
SVD

See more at http://mathworld.wolfram.com/SingularValueDecomposition.html.

Principal Component Analysis

It is to maximize the variance of the data projected to some line, which means compress the information to some line as much as possible.

Let $X=(X_1, X_2, \dots, X_n)^{T}$ be random variable and $\Sigma = ({\sigma}{ij})$ be the variance-covariance matrix of $X$. We want to find the linear combination of $X_1, X_2, \dots, X_n$, i.e. $Y=w^{T}X$, so that
$$Y=\arg\max{Y} , var(Y)=w^{T}\Sigma w, \text{s.t.} w^T w={|w|}_2^2=1 .$$ It is a constrained optimization problem. $$L(w,\lambda) = w^{T}\Sigma w + \lambda ({|w|}_2^2-1)$$ thus that $\frac{\partial L(w,\lambda)}{\partial w} = \Sigma w-\lambda w=0$ which implies that $\lambda$ must be a eigenvalue of $\Sigma$. i.e. $\Sigma w=\lambda w$.

Gaussian Scatter PCA

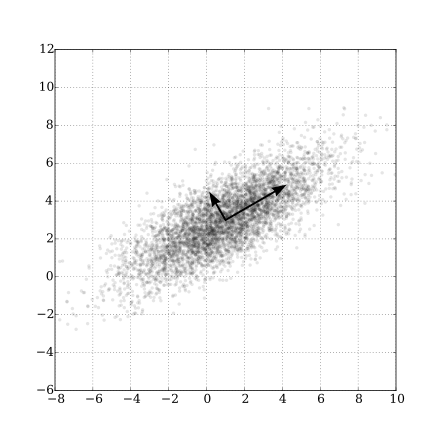Principal Component Regression

In linear regression, we assume that $$f(x|w,b)=w^{T}x + b$$ and we assume that the error ${{y_i - f(x_i|w,b)}}{i=1}^{n}$ are distributed in standard Gaussian distribution. And it is to find the parameters $w,b$ by maximum likelihood function, i.e. $\arg\max{w,b}\sum_{i}(y_i-f(x_i|w,b))^2$. In optimization, we can find the parameters by $\arg\max_{w,b}\sum_{i}d(y_i,f(x_i|w,b))$ where $d(y,l)$ is the distance from the point $y$ to the line $l$, i.e $$ \arg\min_{w,b}\sum_{i=1}^{n}d(x_i, y_i, l) $$ where $d(x_i, y_i)=\frac{|w^{T}x_i+b-y_i|}{\sqrt{w^2+b^2}}$. The problem is that the absolute value function $|\cdot|$ is not differential at original point, so that we may take one subgradient. Another way is to transform the raw data into principal components as a filter. It is the idea of principal component regression. It is more robust than ordinary least square method.

Generalized PCA and SVD

PCA can extend to generalized principal component analysis(GPCA), kernel PCA, functional PCA. The generalized SVD also proposed by Professor Zhang Zhi-Hua. SVD as an matrix composition method is natural to process the tabular data. And the singular values or eigenvalues can be regarded as the importance measure of features or factors. And it used to dimension reduction.