https://leetcode.com/problems/inorder-successor-in-bst-ii/
Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.
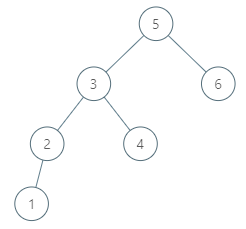
Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
Output: 17
- 这道题要求只给一个 node,然后在 BST 中找到这个节点的后继节点,注意题目没有给出树的结构。
- There are only 3 ways that one node may have a successor
- it has a right child,有右孩子,直接返回右孩子
- it has a parent,
- it is the left child of its parent
- it is the right child of its parent
- 详见代码
"""
# Definition for a Node.
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
"""
class Solution(object):
def inorderSuccessor(self, node):
"""
:type node: Node
:rtype: Node
"""
if not node:
return None
if node.right:
# if node has right child, return most left of right child
node = cur = node.right
while node:
cur = node
node = node.left
return cur
elif node.parent and node.parent.left == node:
# if node is a left child of its parent, return its parent
return node.parent
elif node.parent and node.parent.right == node:
# if node is a right child of its parent,
# reaching to the parent until node is a left child of the parent
# like Example 4, we need to find "13" -> "7" -> "6" -> "15",
# because now "13" is a left child of "15", so we stop finding
while node.parent and node == node.parent.right:
node = node.parent
return node.parent
else:
# no such successor!
return None