Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.
Example 1:
Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into
one [1,5].
- 明确四种情况:
- b 整体在 a 后面,无交集(不用合并)
- b 与 a 部分重叠,需要合并 (a的起点,b的终点)
- b 完全被 a 覆盖 (a的起点,a的终点)
- b 与 a 起点均相同,看谁的终点长。
- 步骤:
- 将所有 intervals 按起点进行排序,保证 a.start <= b.start
- 若发现重叠,即 a.start <= b.start < a.end,也就是b的起点在a的区间内:
- 更改当前 end = max(a.end, b.end),即上图一、图二情况
- 若不重叠,这说明当前 interval 和之前访问过的区间无交集,我们则可以将之前的 [start, end] 加入 result,并将新的 start 和 end 更新为当前 interval 的始末位置。
class Solution(object):
def merge(self, intervals):
"""
:type intervals: List[List[int]]
:rtype: List[List[int]]
"""
if len(intervals) < 2:
return intervals
# sort the intervals by interval.start
intervals.sort(key = lambda x:x[0])
merged_intervals = []
start = intervals[0][0]
end = intervals[0][1]
for i in range(1, len(intervals)):
interval_ = intervals[i]
if interval_[0] <= end:
end = max(end, interval_[1]) # compare a.end or b.end
else:
# b.start > a.end, no need to merge, just append to result
merged_intervals.append([start, end])
# update new start & end with current interval value
start, end = interval_[0], interval_[1]
# finally, add last [start, end] to result
merged_intervals.append([start, end])
return merged_intervalsGiven a list of non-overlapping intervals sorted by their start time, insert a given interval at the correct position and merge all necessary intervals to produce a list that has only mutually exclusive intervals.
Example 1:
Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,6]
Output: [[1,3], [4,7], [8,12]]
Explanation: After insertion, since [4,6] overlaps with [5,7], we merged them into one [4,7].
Example 2:
Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,10]
Output: [[1,3], [4,12]]
Explanation: After insertion, since [4,10] overlaps with [5,7] & [8,12], we merged them into [4,12].
Example 3:
Input: Intervals=[[2,3],[5,7]], New Interval=[1,4]
Output: [[1,4], [5,7]]
Explanation: After insertion, since [1,4] overlaps with [2,3], we merged them into one [1,4].
总结:对于一个排好序的区间序列,插入一个新区间,返回插入且合并后的区间结果。
- 如果用上一道题 Merge Intervals 的方法,先排序,再合并,时间复杂度为 O(N*logN)。但考虑到本题所给区间序列已排好序,我们尝试用 O(N) 的办法一趟完成合并。
- 对第一种情况:也就是 a.end < b.start 的区间,将这些区间直接加入到 result 并跳过即可,直到发现有 overlap 的区间为止。
- 对剩余四种情况,共同特点 a.start < b.end,即必有交集,需要合并:
- 合并后的起点 start,谁在前,谁是 start,即 min(a.start, b.start)
- 合并后的终点 end,谁在后,谁是 end,即 max(a.end, b.end)
class Solution(object):
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
merged, i, start, end = [], 0, 0, 1
while i < len(intervals) and intervals[i][end] < newInterval[start]:
# skip these intervals and append them into merged[]
merged.append(intervals[i])
i += 1
# already find interval do not follow the condition
while i < len(intervals) and intervals[i][start] <= newInterval[end]:
newInterval[start] = min(newInterval[start], intervals[i][start]) # 谁小谁起点
newInterval[end] = max(newInterval[end], intervals[i][end]) # 谁大谁终点
i += 1
merged.append(newInterval) # 合并完,加到merged
# for the rest of intervals
while i < len(intervals):
merged.append(intervals[i])
i += 1
return mergedleetcode 986. Interval List Intersections
Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)
Example 1:
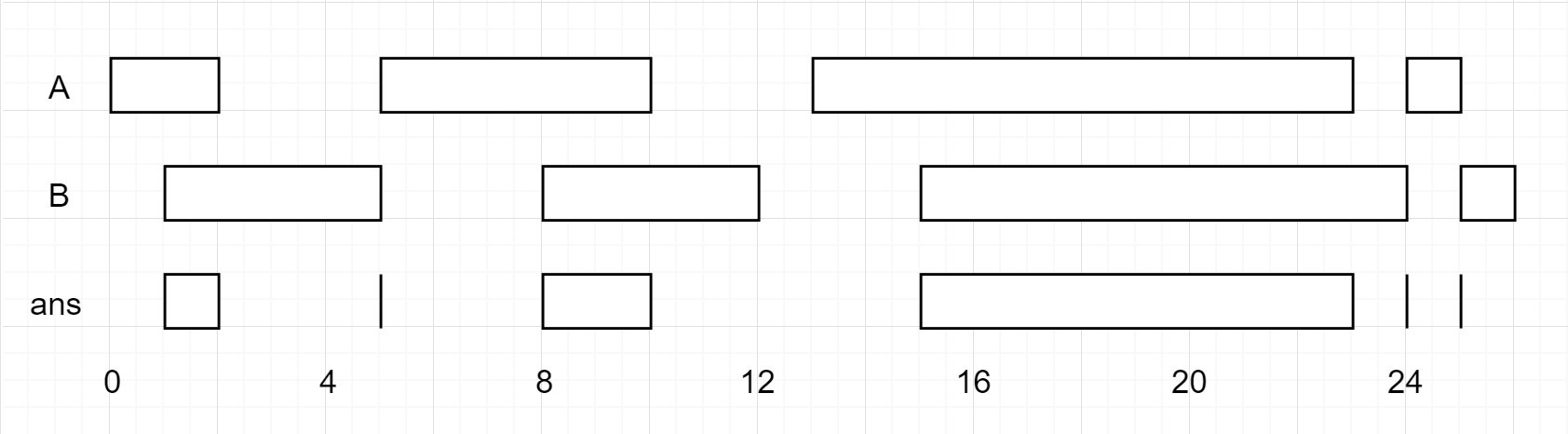
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
与上一题一样,有五种情况:
- while 循环,查找overlap的情况(图2,3,4,5),并对交集作如下操作:
- 更改交集起点 start = max(a.start, b.start)
- 更改交集终点 end = min(a.end, b.end)
class Solution(object):
def intervalIntersection(self, A, B):
"""
:type A: List[List[int]]
:type B: List[List[int]]
:rtype: List[List[int]]
"""
merged, i, j, start, end = [], 0, 0, 0, 1
while i < len(A) and j < len(B):
A_after_B = B[j][start] <= A[i][start] <= B[j][end]
B_after_A = A[i][start] <= B[j][start] <= A[i][end]
if (A_after_B or B_after_A):
intersect_start = max(A[i][start], B[j][start])
intersect_end = min(A[i][end], B[j][end])
merged.append([intersect_start, intersect_end])
if A[i][end] < B[j][end]:
i += 1
else:
j += 1
return merged
-
Time complexity: As we are iterating through both the lists once, the time complexity of the above algorithm is O(N + M), where ‘N’ and ‘M’ are the total number of intervals in the input arrays respectively.
-
Space complexity: Ignoring the space needed for the result list, the algorithm runs in constant space O(1).
Given an array of intervals representing ‘N’ appointments, find out if a person can attend all the appointments.
Example 1:
Appointments: [[1,4], [2,5], [7,9]]
Output: false
Explanation: Since [1,4] and [2,5] overlap, a person cannot attend both of these appointments.
Example 2:
Appointments: [[6,7], [2,4], [8,12]]
Output: true
Explanation: None of the appointments overlap, therefore a person can attend all of them.
Example 3:
Appointments: [[4,5], [2,3], [3,6]]
Output: false
Explanation: Since [4,5] and [3,6] overlap, a person cannot attend both of these appointments.
def can_attend_all_appointments(intervals):
intervals.sort(key=lambda x: x[0])
start, end = 0, 1
for i in range(1, len(intervals)):
if intervals[i][start] < intervals[i-1][end]:
# please note the comparison above, it is "<" and not "<="
# while merging we needed "<=" comparison, as we will be merging the two
# intervals having condition "intervals[i][start] == intervals[i - 1][end]" but
# such intervals don't represent conflicting appointments as one starts right
# after the other
return False
return TrueImplement a
MyCalendarclass to store your events. A new event can be added if adding the event will not cause a double booking.Your class will have the method,
book(int start, int end). Formally, this represents a booking on the half open interval[start, end), the range of real numbersxsuch thatstart <= x < end.A double booking happens when two events have some non-empty intersection (ie., there is some time that is common to both events.)
For each call to the method
MyCalendar.book, returntrueif the event can be added to the calendar successfully without causing a double booking. Otherwise, returnfalseand do not add the event to the calendar.Your class will be called like this:
MyCalendar cal = new MyCalendar();MyCalendar.book(start, end)
Example 1:
MyCalendar(); MyCalendar.book(10, 20); // returns true MyCalendar.book(15, 25); // returns false MyCalendar.book(20, 30); // returns true Explanation: The first event can be booked. The second can't because time 15 is already booked by another event. The third event can be booked, as the first event takes every time less than 20, but not including 20.
- Brute force 暴力搜索,时间复杂度O(n^2)。因为总搜索次数为1+2+3+...+n,每次book都要重头查找一遍
- Binary Search 二分查找,时间复杂度O(n*logn)。
数据结构定义:定义一个orderMap或者TreeMap的数据类型,保存当前已经book的所有pairs,即TreeMap<int, int>,这个Map的映射关系是 start -> end,即 start 为 key,end 为 value。
假定 booked 中已有数据:[(10, 20), (15, 20)],我们这时如果要查询<12, 18>,那么:
floor 定义:Largest entry whose key <= query_key。 即当前小于query_key=12 的最大时间段,就是[10, 20],因为10最接近12
ceiling 定义:smallest entry whose key >query_key。即当前大于query_key=12 的最小时间段,就是[15, 20],因为15刚好大于10
所以我们只需要找两次,即分别找出booked(int start, int end) 时,以start为query_key所对应的floor和celling,在 java/c++ 中这一步操作时间复杂度为 O(logn)。找到 floor 和 ceiling 有何用?
- 以查询<12, 18> 为例,如果我们的query_start=12 比 floor.end (对应 value值) 要小,也就是12<20,则必定overlap。
- 同样,如果我们的ceiling.start 比 end=18 小,也就是15 < 18,也属于overlap。
class MyCalendar {
TreeMap<Integer, Integer> m_booked;
public MyCalendar() {
m_booked = new TreeMap<>();
}
public boolean book(int start, int end) {
Integer largest_key_smaller = m_booked.floorKey(start); // := floor.key
if (largest_key_smaller != null && m_booked.get(largest_key_smaller) > start) {
// lower_bound.end > start, then overlap
return false;
}
Integer smallest_key_larger = m_booked.ceilingKey(start); // := ceiling.key
if (smallest_key_larger != null && smallest_key_larger < end) {
// upper_bound.start < end, then overlap
return false;
}
m_booked.put(start, end); // not overlap, add them to TreeMap
return true;
}
}Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required.
Example 1:
Input: [[0, 30],[5, 10],[15, 20]]
Output: 2
Example 2:
Input: [[7,10],[2,4]]
Output: 1
- 用 Heapq ,每次遇到一个 meeting,先比较 Heap 里面是否存在已经结束的会议,即检查 [s1, e1] 中 e1 <= s2
- 若存在这样已经结束的 meetings,那么就用 Min-Heap 去 pop 这些会议区间
from heapq import *
class Solution(object):
def minMeetingRooms(self, meetings):
meetings.sort(key = lambda x: x[0])
minRooms = 0
minHeap = []
for meet in meetings:
# remove all the meetings that have ended
while (len(minHeap) > 0 and meet[0] >= minHeap[0]):
heappop(minHeap)
# add current meeting into min_heap
heappush(minHeap, meet[1])
# all active meetings are in heap, we need to know the max rooms if happened.
minRooms = max(minRooms, len(minHeap))
return minRoomshttps://leetcode.com/problems/non-overlapping-intervals/
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Example 1:
Input: [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.
Example 2:
Input: [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.
Example 3:
Input: [[1,2],[2,3]]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
- 题意:最少需要移除多少区间,可以使得所有区间都不互相冲突
- 解法:贪心算法
- 排序:先按会议结束的时间排序,然后遍历所有的区间,假如遇到开会时间比 cur_end 要早的区间(即产生冲突的区间),就 count++,代表这个区间是要被移除掉的。如果遇到开会时间比 cur_end 要迟,说明这个区间不会产生冲突,那么就把 cur_end 更新为现在这个非冲突会议的结束时间。
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
cur_end, _count = float('-inf'), 0
for s, e in sorted(intervals, key=lambda x:x[1]):
if s >= cur_end:
cur_end = e
else:
_count += 1
return _counthttps://leetcode.com/problems/remove-covered-intervals/
Given a list of intervals, remove all intervals that are covered by another interval in the list.
Interval [a,b) is covered by interval [c,d) if and only if c <= a and b <= d.
After doing so, return the number of remaining intervals.
Example 1:
Input: intervals = [[1,4],[3,6],[2,8]]
Output: 2
Explanation: Interval [3,6] is covered by [2,8], therefore it is removed.
Example 2:
Input: intervals = [[1,4],[2,3]]
Output: 1
Example 3:
Input: intervals = [[0,10],[5,12]]
Output: 2
Example 4:
Input: intervals = [[3,10],[4,10],[5,11]]
Output: 2
Example 5:
Input: intervals = [[1,2],[1,4],[3,4]]
Output: 1
Constraints:
1 <= intervals.length <= 1000intervals[i].length == 20 <= intervals[i][0] < intervals[i][1] <= 10^5- All the intervals are unique.
- Greedy methods,we first sort the intervals by start time, if two intervals share the same point, we put the longer one to be the first, e.g. [1,2] and [1,4] -> [1,4] and [1,2]
- Then we iterate all the intervals, if the interval[end] > previous_end, we do count++, then update the previous_end.
class Solution:
def removeCoveredIntervals(self, intervals: List[List[int]]) -> int:
# Sort by start point.
# If two intervals share the same start point
# put the longer one to be the first.
intervals.sort(key = lambda x: (x[0], -x[1]))
count = 0
prev_end = 0
for _, end in intervals:
# if current interval is not covered
# by the previous one
if end > prev_end:
count += 1
prev_end = end
return count