Clustering
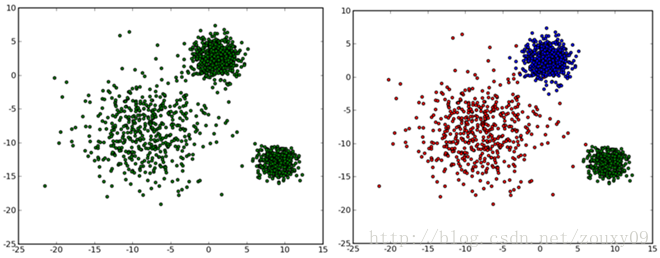
在无监督(无样本标签)情况下的分类,叫做聚类(clustering)。聚类是根据数据之间的关系将数据划分开,如下图,作为一个human,我们可以轻松地区分开 at first glance。
- 预定义聚类的类别数量K
- 随机选择K个数据作为初始中心点
- 迭代直至max_iters或中心无变化
- 计算数据点和所有中心点之间的欧氏距离和
- 将每个数据点划分到最近的类(最近的中心点)
- 计算每一类的新中心点(类中数据求平均)
def fit(self, X_train, max_iters = 10):
centroids = self.initCentroids(X_train, self.n_clusters)
m, n = X_train.shape
for i in range(max_iters): # 迭代次数
print(u'迭代计算次数:%d'%(i+1))
idx = self.findClosestCentroids(X_train, centroids)
centroids = self.computerCentroids(X_train, idx, self.n_clusters) # 重新计算类中心
self.cluster_centers_ = centroids
# init centroids with random samples
def initCentroids(self, data, k):
numSamples, dim = data.shape
centroids = np.zeros((k, dim))
for i in range(k):
index = int(np.random.uniform(0, numSamples))
centroids[i, :] = data[index, :]
return np.array(centroids)
# 找到每条数据距离哪个类中心最近
def findClosestCentroids(self, X, initial_centroids):
m = X.shape[0] # 数据条数
K = initial_centroids.shape[0] # 类的总数
dis = np.zeros((m,K)) # 存储计算每个点分别到K个类的距离
idx = np.zeros((m,1)) # 要返回的每条数据属于哪个类
'''计算每个点到每个类中心的距离'''
for i in range(m):
for j in range(K):
dis[i,j] = np.dot((X[i,:]-initial_centroids[j,:]).reshape(1,-1),(X[i,:]-initial_centroids[j,:]).reshape(-1,1))
'''返回dis每一行的最小值对应的列号,即为对应的类别
- np.min(dis, axis=1)返回每一行的最小值
- np.where(dis == np.min(dis, axis=1).reshape(-1,1)) 返回对应最小值的坐标
- 注意:可能最小值对应的坐标有多个,where都会找出来,所以返回时返回前m个需要的即可(因为对于多个最小值,属于哪个类别都可以)
'''
dummy,idx = np.where(dis == np.min(dis, axis=1).reshape(-1,1))
return idx[0:dis.shape[0]] # 注意截取一下
# 计算类中心
def computerCentroids(self, X,idx,K):
n = X.shape[1]
centroids = np.zeros((K,n))
for i in range(K):
centroids[i,:] = np.mean(X[np.ravel(idx==i),:], axis=0).reshape(1,-1) # 索引要是一维的,axis=0为每一列,idx==i一次找出属于哪一类的,然后计算均值
return centroids