ANN-Basics.md

Artificial neural networks

Artificial neural networks or short: ANN (german: Künstliches Neuronales Netzwerk).

ANNs are no new invention, to the contrary they are comparatively old, but the increasing computation power enables us to calculate bigger and bigger networks, which enables us to attack bigger and bigger problems.

Neurons

Since a ANN is a network or collection of neurons, the question occurs "What is a neuron?".

A neuron is inspired by the structure of a neuron in a human brain. It receives one or more impulses and reacts by outputting a more or less intense signal.

Realization

A neuron is receiving an input-vector (the impulse):

$$ \overrightarrow{x} = \left(\begin{array}{c}x_{0}\ x_{1}\ ...\ x_{n}\end{array}\right) $$

After the neuron receives the input it starts to evaluate the input, by multiplying each input value with an internally saved Weight. When we create a new neural network we normally initialize the weights with random values.

$$ \sum_{i=0}^{n} w_{i} * x_{i} $$

After the input is evaluated the Offset (Bias) gets added, the offset is used as additional parameter to increase the efficiency of the network. The resulting value is the internal state z. When we create a new neural network we normally initialize each bias with the value zero (0).

$$ z = (\sum_{i=0}^{n} w_{i} * x_{i})+b $$

This so calculated internal state gets then passed on to the activation function to calculate the Activation(y) of the Neuron.

$$ y = f(z) $$

In the end the so calculated Activation is passed on to other neurons, commonly of the next layer.

Activation Function

After we evaluate the input, we have a value that has no defined range. This value can be any real value (between $-\infty$ and $+\infty$). But we still have to decide if this value is enough to trigger the neuron to fire or not. Therefore we use the activation function to decide for which range of values the connected neurons will consider this neuron to be fired and for which range they will consider the neuron as not fired. There are different kinds of activation functions, which bring different advantages and disadvantages. Sometimes activation functions are even linked to learning algorithms so you have to use the linked activation function to use this learning algorithm.

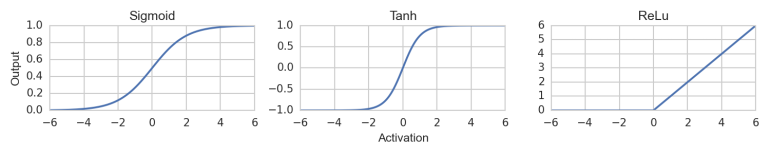
The most common activity functions are the Sigmoid function, the Hyperbolic Tangent and especially the ReLu (Rectifier Linear Unit) function (max(0,x)).

Rectifier linear unit

$$ f(x)= max(x,0) $$

One of the simplest activation functions, that lets the Neuron only fire if the activation is bigger than zero.

• value range: $[0, +\infty]$
• not differentiable everywhere
• continuous

Exponential linear unit

$$ f(x)= \left{\begin{matrix} x& \text{if x}\geq 0 \\ (e^{x}-1)& \text{otherwise} \end{matrix}\right. $$

Exponential modification of the Rectifier, so the Neuron also fires when negative values are given (but weaker).

• value range: $[0, +\infty]$
• differentiable everywhere

Softplus

$$ f(x)= log(e^{x}+1) $$

Tries to perform a smooth approximation on the standard relu-functions.

• returns values in range: $[0, +\infty]$
• everywhere differentiable

Softsign

$$ f(x)= \frac{x}{\left | x \right |+1} $$

• value range: $[-1, +1]$
• differentiable everywhere

Sigmoid

$$ f(x)= \frac{1}{1+ e^{-x}} $$

One of the most spreaded activation functions and the standard activation function in combination with Backpropagation.

• value range: $[0, 1]$
• differentiable everywhere

hyperbolic tangent

$$ f(x)= \tanh(x) = \frac{1 + e^{-2x}}{1 - e^{-2x}} $$

• value range: $[-1, 1]$
• differentiable everywhere

Layers

A neural network consisting of only one neuron is called a Perceptron, but since such a neural network is limited in its use cases, we tend to use neural networks with several layers.

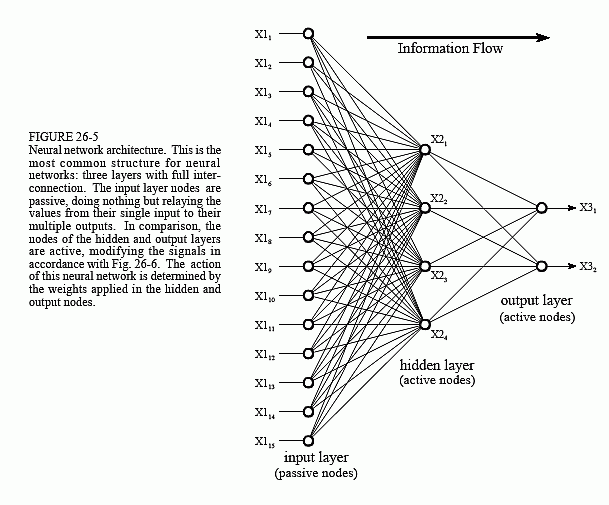
In general you can differ between three kinds of layers

1. The input layer

This Layer is passive, doing nothing but passing the input vector on to the hidden layer.

2. The hidden layer

Every layer that exist between the input layer and output layer is called hidden.

3. The output layer.

This layer returns the values, that represent the output of the whole neural network, therefore the activation function doesn't get applied to this layer, because the evaluation if a neuron should fire or not is unimportant, since the output of the neuron is used as output for the whole network.

A normal neural network has only one input and one output layer, but you can use as many hidden layers as you want. Each additional layer raises the amount of CPU time needed to train and evaluate the network. If your network includes a large number number of layers (i.e., more than 10) it is called a Deep Neural Network.

In a simple artificial neural network each neuron of a layer is connected to every neuron of the next layer. These layers are called Fully Connected Layers.

Convolutional Neural Networks

It's also possible to integrate a case separation into a ANN, this option is common for the extraction of features from a data set. This case separation is called convolution and is realized through a simple function, but it turned out to be a really strong functionality. Such networks are named Convolutional Neural Networks (or short ConvNets)

Loss function

We can pass values to our network and calculate an activation based on the random weights but we could do the same thing with a piece of paper and a few dies. But before we implement the most well known ability of an AI, namely to learn, we first need to know evaluate the correctness of the AI.

Classification

ANN can be used to sort inputs into different classes. A simple classification problem might only have two states (true or false). The ANN therefore either gets the class correct or not. To evaluate your AI you can just count how many correct predictions the AI made (the more the better).

For a classifier it's also useful to use a softmax function as the last layer to transform the actual activations of the previous layer into a probability (from 0 to 1).

Softmax Function

This function is used to reduce a K-dimensional vector z of arbitrary real numbers:

$$ z = \left(\begin{array}{c}z_{0}\ z_{1}\ ...\ z_{K}\end{array}\right) e.g.: \left(\begin{array}{c}80.06\ -200\ -50.2\ 0\end{array}\right) $$

to a K-dimensional vector of real values between [0, 1] that add up to one.

$$ \sigma(z) = \left(\begin{array}{c} \sigma(z){0}\ \sigma(z){1} \ ...\ \sigma(z)_{K}\end{array}\right) e.g.: \left(\begin{array}{c}0.5\ 0.05\0.05\ 0.4\end{array}\right) $$

$$ 1 = \sum_{i = 0}^{K} \sigma(z)_{i} $$

$$ \text{for example:} ~~ 1 = 0.5 + 0.05 + 0.05 + 0.4 $$

Regression

In this case we expect our network to return an estimated or predicted response (mostly a value or a set of values). We need a different loss function for calculate the loss. Commonly we will therefore use L1 were we just use the difference between the expected and the returned output. Mostly to create a more neutral loss we take the square of the difference this loss function is then called L2. In some cases it can also become handy to use Cross Entropy as a loss function.

Learning

After we defined which cases our network got right or wrong, we can start to teach it. Note that you naturally have to first collect fitting training and test data for your network. After that you train your network by giving the network one set of your training data to process. Since we initialized the weights of the neurons with random values it is unlikely that the output is similar to the expected output. To change that we start to tune our network using our loss function. There are several different technics how to do that, I will introduce some of them in a different file.

Representation as Matrix

It's possible to represent a neural network as sequence of matrices. We extract the weight-vectors of the neurons and assemble them in a matrix. Each column of these matrices represents the weights of one neuron. Each Bias gets extracted into a separate vector that gets added during the evaluation. This principle can be applied to every hidden layer as well as the output layer. $$n : \text{length input vector} $$

$$nH : \text{number hidden neurons} $$

$$ \begin{bmatrix} w_{1|1}& w_{1|2} & ... & w_{1|n} \\ w_{2|1}& w_{2|2} & ... & w_{2|n} \\ ... & ... & ... & ... \\ w_{nH|1} & w_{nH|2} & ... & w_{nH|n} \end{bmatrix} $$

$$ nO : \text{number of output neurons} $$

$$ \begin{bmatrix} w_{1|1}& w_{1|2} & ... & w_{1|nH} \\ w_{2|1}& w_{2|2} & ... & w_{2|nH} \\ ... & ... & ... & ... \\ w_{nO|1} & w_{nO|2} & ... & w_{nO|nH} \end{bmatrix} $$

Book recommendations

The Elements of Statistical Learning by Trevor Hastie, Robert Tibshirani, Jerome Friedman

Neural Networks by Raul Rojas (available online)