Skip to content
/ Matft Public
forked from jjjkkkjjj/Matft

Numpy-like library in swift. (Multi-dimensional Array, ndarray, matrix and vector library)

0 stars 21 forks Branches Tags Activity
Star
Notifications You must be signed in to change notification settings

Synopsis/Matft

BranchesTags
 
 

Repository files navigation

Matft

SwiftPM compatible CocoaPods compatible Carthage compatible license

Matft is Numpy-like library in Swift. Function name and usage is similar to Numpy.

INFO: Support Complex!!

Note: You can use [Protocol version(beta version)](https://github.com/jjjkkkjjj/Matft/tree/protocol) too.

Feature & Usage

  • Many types

  • Pretty print

  • Indexing

    • Positive
    • Negative
    • Boolean
    • Fancy
    • Complex

  • Slicing

    • Start / To / By
    • New Axis

  • View

    • Assignment

  • Conversion

    • Broadcast
    • Transpose
    • Reshape
    • Astype

  • Univarsal function reduction

  • Mathematic

    • Arithmetic
    • Statistic
    • Linear Algebra

  • Complex

  • Image Conversion

...etc.

See Function List for all functions.

Declaration

MfArray

  • The MfArray such like a numpy.ndarray

    let a = MfArray([[[ -8,  -7,  -6,  -5],
                  [ -4,  -3,  -2,  -1]],
        
                 [[ 0,  1,  2,  3],
                  [ 4,  5,  6,  7]]])
let aa = Matft.arange(start: -8, to: 8, by: 1, shape: [2,2,4])
print(a)
print(aa)
/*
mfarray = 
[[[	-8,		-7,		-6,		-5],
[	-4,		-3,		-2,		-1]],

[[	0,		1,		2,		3],
[	4,		5,		6,		7]]], type=Int, shape=[2, 2, 4]
mfarray = 
[[[	-8,		-7,		-6,		-5],
[	-4,		-3,		-2,		-1]],

[[	0,		1,		2,		3],
[	4,		5,		6,		7]]], type=Int, shape=[2, 2, 4]
*/

MfType

  • You can pass MfType as MfArray's argument mftype: .Hoge . It is similar to dtype.

    ※Note that stored data type will be Float or Double only even if you set MfType.Int. So, if you input big number to MfArray, it may be cause to overflow or strange results in any calculation (+, -, *, /,... etc.). But I believe this is not problem in practical use.

  • MfType's list is below

      public enum MfType: Int{
    case None // Unsupportted
    case Bool
    case UInt8
    case UInt16
    case UInt32
    case UInt64
    case UInt
    case Int8
    case Int16
    case Int32
    case Int64
    case Int
    case Float
    case Double
    case Object // Unsupported
}

  • Also, you can convert MfType easily using astype

    let a = MfArray([[[ -8,  -7,  -6,  -5],
                  [ -4,  -3,  -2,  -1]],
        
                 [[ 0,  1,  2,  3],
                  [ 4,  5,  6,  7]]])
print(a)//See above. if mftype is not passed, MfArray infer MfType. In this example, it's MfType.Int

let a = MfArray([[[ -8,  -7,  -6,  -5],
                  [ -4,  -3,  -2,  -1]],
            
                 [[ 0,  1,  2,  3],
                  [ 4,  5,  6,  7]]], mftype: .Float)
print(a)
/*
mfarray = 
[[[	-8.0,		-7.0,		-6.0,		-5.0],
[	-4.0,		-3.0,		-2.0,		-1.0]],

[[	0.0,		1.0,		2.0,		3.0],
[	4.0,		5.0,		6.0,		7.0]]], type=Float, shape=[2, 2, 4]
*/
let aa = MfArray([[[ -8,  -7,  -6,  -5],
                  [ -4,  -3,  -2,  -1]],
            
                 [[ 0,  1,  2,  3],
                  [ 4,  5,  6,  7]]], mftype: .UInt)
print(aa)
/*
mfarray = 
[[[	4294967288,		4294967289,		4294967290,		4294967291],
[	4294967292,		4294967293,		4294967294,		4294967295]],

[[	0,		1,		2,		3],
[	4,		5,		6,		7]]], type=UInt, shape=[2, 2, 4]
*/
//Above output is same as numpy!
/*
>>> np.arange(-8, 8, dtype=np.uint32).reshape(2,2,4)
array([[[4294967288, 4294967289, 4294967290, 4294967291],
        [4294967292, 4294967293, 4294967294, 4294967295]],

       [[         0,          1,          2,          3],
        [         4,          5,          6,          7]]], dtype=uint32)
*/

print(aa.astype(.Float))
/*
mfarray = 
[[[	-8.0,		-7.0,		-6.0,		-5.0],
[	-4.0,		-3.0,		-2.0,		-1.0]],

[[	0.0,		1.0,		2.0,		3.0],
[	4.0,		5.0,		6.0,		7.0]]], type=Float, shape=[2, 2, 4]
*/

Subscription

MfSlice

  • You can access specific data using subscript.

You can set MfSlice (see below's list) to subscript.

  • MfSlice(start: Int? = nil, to: Int? = nil, by: Int = 1)
  • Matft.newaxis
  • ~< //this is prefix, postfix and infix operator. same as python's slice, ":"
  • Matft.all // same as python's slice :, matft's 0~<
  • Matft.reverse // same as python's slice ::-1, matft's ~<<-1

(Positive) Indexing

  • Normal indexing

    let a = Matft.arange(start: 0, to: 27, by: 1, shape: [3,3,3])
print(a)
/*
mfarray = 
[[[	0,		1,		2],
[	3,		4,		5],
[	6,		7,		8]],

[[	9,		10,		11],
[	12,		13,		14],
[	15,		16,		17]],

[[	18,		19,		20],
[	21,		22,		23],
[	24,		25,		26]]], type=Int, shape=[3, 3, 3]
*/
print(a[2,1,0])
// 21

    Slicing

  • If you replace : with ~<, you can get sliced mfarray. Note that use a[0~<] instead of a[:] to get all elements along axis.

    print(a[~<1])  //same as a[:1] for numpy
/*
mfarray = 
[[[	9,		10,		11],
[	12,		13,		14],
[	15,		16,		17]]], type=Int, shape=[1, 3, 3]
*/
print(a[1~<3]) //same as a[1:3] for numpy
/*
mfarray = 
[[[	9,		10,		11],
[	12,		13,		14],
[	15,		16,		17]],

[[	18,		19,		20],
[	21,		22,		23],
[	24,		25,		26]]], type=Int, shape=[2, 3, 3]
*/
print(a[~<~<2]) //same as a[::2] for numpy
//print(a[~<<2]) //alias
/*
mfarray = 
[[[	0,		1,		2],
[	3,		4,		5],
[	6,		7,		8]],

[[	18,		19,		20],
[	21,		22,		23],
[	24,		25,		26]]], type=Int, shape=[2, 3, 3]
*/

print(a[Matft.all, 0]) //same as a[:, 0] for numpy
/*
mfarray = 
[[    0,      1,      2],
[ 9,      10,     11],
[18,      19,     20]], type=Int, shape=[3, 3]
*/

Negative Indexing

  • Negative indexing is also available That's implementation was hardest for me...

    print(a[~<-1])
/*
mfarray = 
[[[	0,		1,		2],
[	3,		4,		5],
[	6,		7,		8]],

[[	9,		10,		11],
[	12,		13,		14],
[	15,		16,		17]]], type=Int, shape=[2, 3, 3]
*/
print(a[-1~<-3])
/*
mfarray = 
	[], type=Int, shape=[0, 3, 3]
*/
print(a[Matft.reverse])
//print(a[~<~<-1]) //alias
//print(a[~<<-1]) //alias
/*
mfarray = 
[[[	18,		19,		20],
[	21,		22,		23],
[	24,		25,		26]],

[[	9,		10,		11],
[	12,		13,		14],
[	15,		16,		17]],

[[	0,		1,		2],
[	3,		4,		5],
[	6,		7,		8]]], type=Int, shape=[3, 3, 3]*/

Boolean Indexing

  • You can use boolean indexing.

    Caution! I don't check performance, so this boolean indexing may be slow

    Unfortunately, Matft is too slower than numpy...

    (numpy is 1ms, Matft is 7ms...)

    let img = MfArray([[1, 2, 3],
                               [4, 5, 6],
                               [7, 8, 9]], mftype: .UInt8)
img[img > 3] = MfArray([10], mftype: .UInt8)
print(img)
/*
mfarray = 
[[	1,		2,		3],
[	10,		10,		10],
[	10,		10,		10]], type=UInt8, shape=[3, 3]
*/

Fancy Indexing

  • You can use fancy indexing!!!

    let a = MfArray([[1, 2], [3, 4], [5, 6]])
            
a[MfArray([0, 1, 2]), MfArray([0, -1, 0])] = MfArray([999,888,777])
print(a)
/*
mfarray = 
[[	999,		2],
[	3,		888],
[	777,		6]], type=Int, shape=[3, 2]
*/
            
a.T[MfArray([0, 1, -1]), MfArray([0, 1, 0])] = MfArray([-999,-888,-777])
print(a)
/*
mfarray = 
[[	-999,		-777],
[	3,		-888],
[	777,		6]], type=Int, shape=[3, 2]
*/

View

  • Note that returned subscripted mfarray will have base property (is similar to view in Numpy). See numpy doc in detail.

    let a = Matft.arange(start: 0, to: 4*4*2, by: 1, shape: [4,4,2])
            
let b = a[0~<, 1]
b[~<<-1] = MfArray([9999]) // cannot pass Int directly such like 9999

print(a)
/*
mfarray = 
[[[	0,		1],
[	9999,		9999],
[	4,		5],
[	6,		7]],

[[	8,		9],
[	9999,		9999],
[	12,		13],
[	14,		15]],

[[	16,		17],
[	9999,		9999],
[	20,		21],
[	22,		23]],

[[	24,		25],
[	9999,		9999],
[	28,		29],
[	30,		31]]], type=Int, shape=[4, 4, 2]
*/

Complex

Matft supports Complex!!

But this is beta version. so, any bug may be ocurred.

Please report me by issue!

TODO

  • Arithmetic Operation
  • Angle, Conjugate and Absolute
  • Math (partial: sin,cos,tan,exp,log)
  • Basic Subscription Getter
  • Basic Subscription Setter
  • Boolean Indexing Getter
  • Boolean Indexing Setter
  • Fancy Indexing Getter
  • Fancy Indexing Setter
let real = Matft.arange(start: 0, to: 16, by: 1).reshape([2,2,4])
let imag = Matft.arange(start: 0, to: -16, by: -1).reshape([2,2,4])
let a = MfArray(real: real, imag: imag)
print(a)

/*
mfarray = 
[[[    0 +0j,        1 -1j,        2 -2j,        3 -3j],
[    4 -4j,        5 -5j,        6 -6j,        7 -7j]],

[[    8 -8j,        9 -9j,        10 -10j,        11 -11j],
[    12 -12j,        13 -13j,        14 -14j,        15 -15j]]], type=Int, shape=[2, 2, 4]
*/

print(a+a)
/*
mfarray = 
[[[    0 +0j,        2 -2j,        4 -4j,        6 -6j],
[    8 -8j,        10 -10j,        12 -12j,        14 -14j]],

[[    16 -16j,        18 -18j,        20 -20j,        22 -22j],
[    24 -24j,        26 -26j,        28 -28j,        30 -30j]]], type=Int, shape=[2, 2, 4]
*/

print(Matft.complex.angle(a))
/*
mfarray = 
[[[    -0.0,        -0.7853982,        -0.7853982,        -0.7853982],
[    -0.7853982,        -0.7853982,        -0.7853982,        -0.7853982]],

[[    -0.7853982,        -0.7853982,        -0.7853982,        -0.7853982],
[    -0.7853982,        -0.7853982,        -0.7853982,        -0.7853982]]], type=Float, shape=[2, 2, 4]
*/

print(Matft.complex.conjugate(a))
/*
mfarray = 
[[[    0 +0j,        1 +1j,        2 +2j,        3 +3j],
[    4 +4j,        5 +5j,        6 +6j,        7 +7j]],

[[    8 +8j,        9 +9j,        10 +10j,        11 +11j],
[    12 +12j,        13 +13j,        14 +14j,        15 +15j]]], type=Int, shape=[2, 2, 4]
*/

Image

You can acheive an image processing by Matft! (Beta version) Please refer to the example here.

@IBOutlet weak var originalImageView: UIImageView!
@IBOutlet weak var reverseImageView: UIImageView!
@IBOutlet weak var swapImageView: UIImageView!

func reverse(){
    var image = Matft.image.cgimage2mfarray(self.reverseImageView.image!.cgImage!)

    // reverse
    image = image[Matft.reverse] // same as image[~<<-1]
    self.reverseImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
}


func swapchannel(){
    var image = Matft.image.cgimage2mfarray(self.swapImageView.image!.cgImage!)

    // swap channel
    image = image[Matft.all, Matft.all, MfArray([1,0,2,3])] // same as image[0~<, 0~<, MfArray([1,0,2,3])]
    self.swapImageView.image = UIImage(cgImage: Matft.image.mfarray2cgimage(image))
}

For more complex conversion, see OpenCV code.

Screen Shot 2022-07-19 at 21 09 02

Function List

Below is Matft's function list. As I mentioned above, almost functions are similar to Numpy. Also, these function use Accelerate framework inside, the perfomance may keep high.

* means method function exists too. Shortly, you can use a.shallowcopy() where a is MfArray.

^ means method function only. Shortly, you can use a.tolist() not Matft.tolist where a is MfArray.

# means support complex operation

  • Creation
Matft Numpy
*#Matft.shallowcopy *numpy.copy
*#Matft.deepcopy copy.deepcopy
Matft.nums numpy.ones * N
Matft.nums_like numpy.ones_like * N
Matft.arange numpy.arange
Matft.eye numpy.eye
Matft.diag numpy.diag
Matft.vstack numpy.vstack
Matft.hstack numpy.hstack
Matft.concatenate numpy.concatenate
*Matft.append numpy.append
*Matft.insert numpy.insert
*Matft.take numpy.take
  • Conversion
Matft Numpy
*#Matft.astype *numpy.astype
*#Matft.transpose *numpy.transpose
*#Matft.expand_dims *numpy.expand_dims
*#Matft.squeeze *numpy.squeeze
*#Matft.broadcast_to *numpy.broadcast_to
*#Matft.to_contiguous *numpy.ascontiguousarray
*#Matft.flatten *numpy.flatten
*#Matft.flip *numpy.flip
*#Matft.clip *numpy.clip
*#Matft.swapaxes *numpy.swapaxes
*#Matft.moveaxis *numpy.moveaxis
*Matft.roll numpy.roll
*Matft.sort *numpy.sort
*Matft.argsort *numpy.argsort
^MfArray.toArray ^numpy.ndarray.tolist
^MfArray.toFlattenArray n/a
*Matft.orderedUnique numpy.unique
  • File
Matft Numpy
Matft.file.loadtxt numpy.loadtxt
Matft.file.genfromtxt numpy.genfromtxt
Matft.file.savetxt numpy.savetxt

  • Operation

    Line 2 is infix (prefix) operator.

Matft Numpy
#Matft.add
+		 numpy.add
+
#Matft.sub
-		 numpy.sub
-
#Matft.div
/		 numpy.div
.
#Matft.mul
*		 numpy.multiply
*
Matft.inner
*+		 numpy.inner
n/a
Matft.cross
*^		 numpy.cross
n/a
Matft.matmul
*&　　		 numpy.matmul
@　
Matft.dot　　　 numpy.dot 　
Matft.equal
===		 numpy.equal
==
Matft.not_equal
!==		 numpy.not_equal
!=
Matft.less
<		 numpy.less
<
Matft.less_equal
<=		 numpy.less_equal
<=
Matft.greater
>		 numpy.greater
>
Matft.greater_equal
>=		 numpy.greater_equal
>=
#Matft.allEqual
==		 numpy.array_equal
n/a
#Matft.neg
-		 numpy.negative
-
  • Universal Fucntion Reduction
Matft Numpy
*#Matft.ufuncReduce
e.g.) Matft.ufuncReduce(a, Matft.add)		 numpy.add.reduce
e.g.) numpy.add.reduce(a)
*#Matft.ufuncAccumulate
e.g.) Matft.ufuncAccumulate(a, Matft.add)		 numpy.add.accumulate
e.g.) numpy.add.accumulate(a)
  • Math function
Matft Numpy
#Matft.math.sin numpy.sin
Matft.math.asin numpy.asin
Matft.math.sinh numpy.sinh
Matft.math.asinh numpy.asinh
#Matft.math.cos numpy.cos
Matft.math.acos numpy.acos
Matft.math.cosh numpy.cosh
Matft.math.acosh numpy.acosh
#Matft.math.tan numpy.tan
Matft.math.atan numpy.atan
Matft.math.tanh numpy.tanh
Matft.math.atanh numpy.atanh
Matft.math.sqrt numpy.sqrt
Matft.math.rsqrt numpy.rsqrt
#Matft.math.exp numpy.exp
#Matft.math.log numpy.log
Matft.math.log2 numpy.log2
Matft.math.log10 numpy.log10
*Matft.math.ceil numpy.ceil
*Matft.math.floor numpy.floor
*Matft.math.trunc numpy.trunc
*Matft.math.nearest numpy.nearest
*Matft.math.round numpy.round
#Matft.math.abs numpy.abs
Matft.math.reciprocal numpy.reciprocal
#Matft.math.power numpy.power
Matft.math.arctan2 numpy.arctan2
Matft.math.square numpy.square
Matft.math.sign numpy.sign
  • Statistics function
Matft Numpy
*Matft.stats.mean *numpy.mean
*Matft.stats.max *numpy.max
*Matft.stats.argmax *numpy.argmax
*Matft.stats.min *numpy.min
*Matft.stats.argmin *numpy.argmin
*Matft.stats.sum *numpy.sum
Matft.stats.maximum numpy.maximum
Matft.stats.minimum numpy.minimum
*Matft.stats.sumsqrt n/a
*Matft.stats.squaresum n/a
*Matft.stats.cumsum *numpy.cumsum
  • Random function
Matft Numpy
Matft.random.rand numpy.random.rand
Matft.random.randint numpy.random.randint
  • Linear algebra
Matft Numpy
Matft.linalg.solve numpy.linalg.solve
Matft.linalg.inv numpy.linalg.inv
Matft.linalg.det numpy.linalg.det
Matft.linalg.eigen numpy.linalg.eig
Matft.linalg.svd numpy.linalg.svd
Matft.linalg.pinv numpy.linalg.pinv
Matft.linalg.polar_left scipy.linalg.polar
Matft.linalg.polar_right scipy.linalg.polar
Matft.linalg.normlp_vec scipy.linalg.norm
Matft.linalg.normfro_mat scipy.linalg.norm
Matft.linalg.normnuc_mat scipy.linalg.norm
  • Complex
Matft Numpy
Matft.complex.angle numpy.angle
Matft.complex.conjugate numpy.conj / numpy.conjugate
Matft.complex.abs numpy.abs / numpy.absolute
  • Interpolation

Matft supports only natural cubic spline. I'll implement other boundary condition later.

Matft Numpy
Matft.interp1d.cubicSpline scipy.interpolation.CubicSpline
  • Image
Matft Numpy
Matft.image.cgimage2mfarray N/A
Matft.image.mfarray2cgimage N/A
Matft OpenCV
Matft.image.color cv2.cvtColor
Matft.image.resize cv2.resize
Matft.image.warpAffine cv2.warpAffine

Performance

I use Accelerate framework, so all of MfArray operation may keep high performance.

let a = Matft.arange(start: 0, to: 10*10*10*10*10*10, by: 1, shape: [10,10,10,10,10,10])
let aneg = Matft.arange(start: 0, to: -10*10*10*10*10*10, by: -1, shape: [10,10,10,10,10,10])
let aT = a.T
let b = a.transpose(axes: [0,3,4,2,1,5])
let c = a.transpose(axes: [1,2,3,4,5,0])
let posb = a > 0
import numpy as np

a = np.arange(10**6).reshape((10,10,10,10,10,10))
aneg = np.arange(0, -10**6, -1).reshape((10,10,10,10,10,10))
aT = a.T
b = a.transpose((0,3,4,2,1,5))
c = a.transpose((1,2,3,4,5,0))
posb = a > 0
  • Arithmetic test
Matft time Numpy time
let _ = a+aneg 596μs a+aneg 1.04ms
let _ = b+aT 4.46ms b+aT 4.31ms
let _ = c+aT 5.31ms c+aT 2.92ms
  • Math test
Matft time Numpy time
let _ = Matft.math.sin(a) 2.14ms np.sin(a) 14.7ms
let _ = Matft.math.sin(b) 7.02ms np.sin(b) 15.8ms
let _ = Matft.math.sign(a) 3.09ms np.sign(a) 1.37ms
let _ = Matft.math.sign(b) 8.33ms np.sign(b) 1.42ms
  • Bool test
Matft time Numpy time
let _ = a > 0 4.63ms a > 0 855μs
let _ = a > b 17.8ms a > b 1.83ms
let _ = a === 0 4.65ms a == 0 603μs
let _ = a === b 19.7ms a == b 1.78ms
  • Indexing test
Matft time Numpy time
let _ = a[posb] 1.21ms a[posb] 1.29ms

Matft achieved almost same performance as Numpy!!!

※Swift's performance test was conducted in release mode

However, as you can see the above table, Matft's boolean operation is toooooooo slow...(Issue #18)

So, a pull request is very welcome!!

Installation

SwiftPM

  • Import
    • Project > Build Setting > + Build Setting
    • Select Rules select
  • Update
    • File >Swift Packages >Update to Latest Package versions update

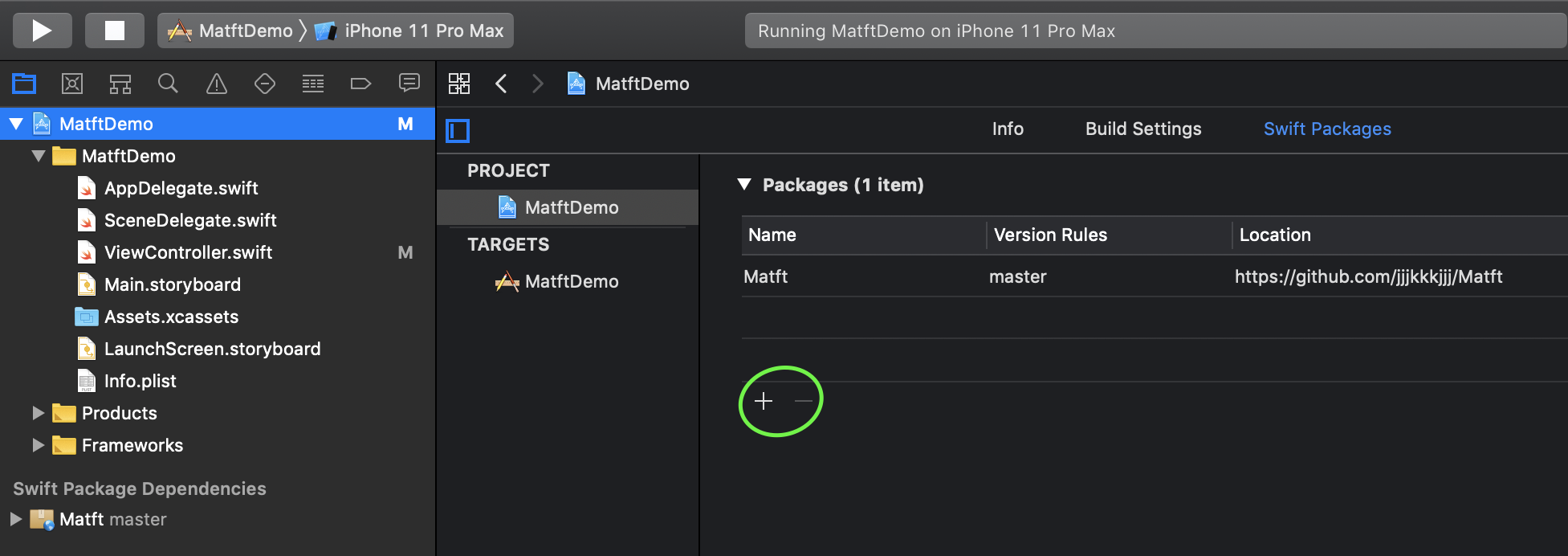
Important!!! the below installation is outdated. Please install Matft via swiftPM!!!

Carthage

  • Set Cartfile

    echo 'github "jjjkkkjjj/Matft"' > Cartfile
 carthage update ###or append '--platform ios'

  • Import Matft.framework made by above process to your project

CocoaPods

  • Create Podfile (Skip if you have already done)

    pod init

  • Write pod 'Matft' in Podfile such like below

    target 'your project' do
  pod 'Matft'
end

  • Install Matft

    pod install

Contact

Feel free to ask this project or anything via junnosuke.kado.git@gmail.com

About

Numpy-like library in swift. (Multi-dimensional Array, ndarray, matrix and vector library)

Resources

Readme
Activity
Custom properties

Stars

0 stars

Watchers

0 watching

Forks

0 forks
Report repository

Releases

21 tags

Packages

No packages published