05 Example: NP-Complete.md

Example: XKCD's NP-Complete

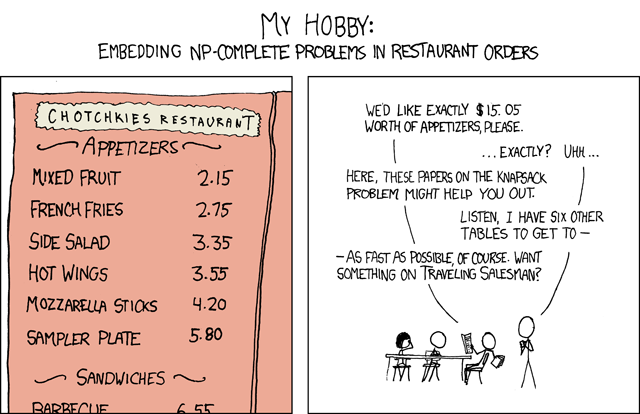
Mathematically, this problem is asking for:

$$ 15.05 = 2.15 * Count_{mixed fruit} + 2.75 * Count_{french fries} + 3.35 * Count_{side salad} + 3.55 * Count_{hot wings} + 4.20 * Count_{mozzarella sticks} + 5.80 * Count_{sampler plate} $$

If we declare a constant Int for each of these, constrained that the values must be non-negative and that this equation holds, it should work:

(declare-const mixed_fruit Int)
(declare-const french_fries Int)
(declare-const side_salad Int)
(declare-const hot_wings Int)
(declare-const mozzarella_sticks Int)
(declare-const sampler_plate Int)

(assert (>= mixed_fruit 0))
(assert (>= french_fries 0))
(assert (>= side_salad 0))
(assert (>= hot_wings 0))
(assert (>= mozzarella_sticks 0))
(assert (>= sampler_plate 0))

(assert (= 15.05
        (+
         (* 2.15 mixed_fruit)
         (* 2.75 french_fries)
         (* 3.35 side_salad)
         (* 3.55 hot_wings)
         (* 4.20 mozzarella_sticks)
         (* 5.80 sampler_plate)
        )))

(check-sat)
sat

(get-model)
(
  (define-fun sampler_plate () Int
    1)
  (define-fun mozzarella_sticks () Int
    0)
  (define-fun french_fries () Int
    0)
  (define-fun side_salad () Int
    0)
  (define-fun mixed_fruit () Int
    1)
  (define-fun hot_wings () Int
    2)
)

Note that there exists another solution:

(
  (define-fun sampler_plate () Int
    0)
  (define-fun mozzarella_sticks () Int
    0)
  (define-fun french_fries () Int
    0)
  (define-fun side_salad () Int
    0)
  (define-fun hot_wings () Int
    0)
  (define-fun mixed_fruit () Int
    7)
)

Python implementation

This Python implementation requires the use of the ToReal function to ensure the primary assertion uses Real sorts instead of downcasting to an Int sort.

from z3 import *
sampler, mozzarella, fries, salad, wings, fruit = \
        Ints('sampler_plate mozzarella_sticks french_fries side_salad hot_wings mixed_fruit')

s = Solver()

for item in [sampler, mozzarella, fries, salad, wings, fruit]:
	s.add(item >= 0)

s.add(15.05 == 2.15 * ToReal(fruit)     
             + 2.75 * ToReal(fries)     
             + 3.35 * ToReal(salad)     
             + 3.55 * ToReal(wings)     
             + 4.20 * ToReal(mozzarella)
             + 5.80 * ToReal(sampler))

assert sat == s.check()

s.model() # [sampler_plate = 0,
          #  mozzarella_sticks = 0,
          #  french_fries = 0,
          #  side_salad = 0,
          #  hot_wings = 0,
          #  mixed_fruit = 7]

---

With a few basic examples under our belt, let's turn next to Functions in SMT-LIB.