-
Notifications
You must be signed in to change notification settings - Fork 236
API Reference
This page describes the concepts in graphlib and provides a reference for the API. By default, graphlib functions and objects are exposed under the graphlib namespace.
Table of Contents
Graphlib has a single graph type: Graph. To create a new instance:
var g = new Graph();By default this will create a directed graph that does not allow multi-edges or compound nodes. The following options can be used when constructing a new graph:
-
directed: set to
trueto get a directed graph andfalseto get an undirected graph. An undirected graph does not treat the order of nodes in an edge as significant. In other words,g.edge("a", "b") === g.edge("b", "a")for an undirected graph. Default:true. -
multigraph: set to
trueto allow a graph to have multiple edges between the same pair of nodes. Default:false. -
compound: set to
trueto allow a graph to have compound nodes - nodes which can be the parent of other nodes. Default:false.
To set the options, pass in an options array to the Graph constructor. For example, to create a directed compound multigraph:
var g = new Graph({ directed: true, compound: true, multigraph: true });In graphlib, a node is represented by a user-supplied String id. All node related functions use this String id as a way to uniquely identify the node. Here is an example of interacting with nodes:
var g = new Graph();
g.setNode("my-id", "my-label");
g.node("my-id"); // returns "my-label"Edges in graphlib are identified by the nodes they connect. For example:
var g = new Graph();
g.setEdge("source", "target", "my-label");
g.edge("source", "target"); // returns "my-label"However, we need a way to uniquely identify an edge in a single object for various edge queries (e.g. outEdges). We use edgeObjs for this purpose. They consist of the following properties:
- v: the id of the source or tail node of an edge
- w: the id of the target or head node of an edge
- name (optional): the name that uniquely identifies a multi-edge.
Any edge function that takes an edge id will also work with an edgeObj. For example:
var g = new Graph();
g.setEdge("source", "target", "my-label");
g.edge({ v: "source", w: "target" }); // returns "my-label"A multigraph is a graph that can have more than one edge between the same pair of nodes. By default graphlib graphs are not multigraphs, but a multigraph can be constructed by setting the multigraph property to true:
var g = new Graph({ multigraph: true });With multiple edges between two nodes we need some way to uniquely identify each edge. We call this the name property. Here's an example of creating a couple of edges between the same nodes:
var g = new Graph({ multigraph: true });
g.setEdge("a", "b", "edge1-label", "edge1");
g.setEdge("a", "b", "edge2-label", "edge2");
g.getEdge("a", "b", "edge1"); // returns "edge1-label"
g.getEdge("a", "b", "edge2"); // returns "edge2-label"
g.edges(); // returns [{ v: "a", w: "b", name: "edge1" },
// { v: "a", w: "b", name: "edge2" }]A multigraph still allows an edge with no name to be created:
var g = new Graph({ multigraph: true });
g.setEdge("a", "b", "my-label");
g.edge({ v: "a", w: "b" }); // returns "my-label"A compound graph is one where a node can be the parent of other nodes. The child nodes form a "subgraph". Here's an example of constructing and interacting with a compound graph:
var g = new Graph({ compound: true });
g.setParent("a", "parent");
g.setParent("b", "parent");
g.parent("a"); // returns "parent"
g.parent("b"); // returns "parent"
g.parent("parent"); // returns undefinedWhen a node or edge is created without a label, a default label can be assigned. See setDefaultNodeLabel and setDefaultEdgeLabel.
# graph.isDirected()
Returns true if the graph is directed. A directed graph treats the order of nodes in an edge as significant whereas an undirected graph does not. This example demonstrates the difference:
var directed = new Graph({ directed: true });
directed.setEdge("a", "b", "my-label");
directed.edge("a", "b"); // returns "my-label"
directed.edge("b", "a"); // returns undefined
var undirected = new Graph({ directed: false });
undirected.setEdge("a", "b", "my-label");
undirected.edge("a", "b"); // returns "my-label"
undirected.edge("b", "a"); // returns undefined# graph.isMultigraph()
Returns true if the graph is a multigraph.
# graph.isCompound()
Returns true if the graph is compound.
# graph.graph()
Returns the currently assigned label for the graph. If no label has been assigned, returns undefined. Example:
var g = new Graph();
g.graph(); // returns undefined
g.setGraph("graph-label");
g.graph(); // returns "graph-label"# graph.setGraph(label)
Sets the label for the graph to label.
# graph.nodeCount()
Returns the number of nodes in the graph.
# graph.edgeCount()
Returns the number of edges in the graph.
# graph.setDefaultNodeLabel(val)
Sets a new default value that is assigned to nodes that are created without a label. If val is not a function it is assigned as the label directly. If val is a function, it is called with the id of the node being created.
# graph.setDefaultEdgeLabel(val)
Sets a new default value that is assigned to edges that are created without a label. If val is not a function it is assigned as the label directly. If val is a function, it is called with the parameters (v, w, name).
# graph.nodes()
Returns the ids of the nodes in the graph. Use node(v) to get the label for each node. Takes O(|V|) time.
# graph.edges()
Returns the [edgeObj](#node-and-edge-representation) for each edge in the graph. Use edge(edgeObj) to get the label for each edge. Takes O(|E|) time.
# graph.sources()
Returns those nodes in the graph that have no in-edges. Takes O(|V|) time.
# graph.sinks()
Returns those nodes in the graph that have no out-edges. Takes O(|V|) time.
# graph.hasNode(v)
Returns true if the graph has a node with the id v. Takes O(1) time.
# graph.node(v)
Returns the label assigned to the node with the id v if it is in the graph. Otherwise returns false. Takes O(1) time.
# graph.setNode(v, [label])
Creates or updates the value for the node v in the graph. If label is supplied it is set as the value for the node. If label is not supplied and the node was created by this call then the default node label will be assigned. Returns the graph, allowing this to be chained with other functions. Takes O(1) time.
# graph.removeNode(v)
Remove the node with the id v in the graph or do nothing if the node is not in the graph. If the node was removed this function also removes any incident edges. Returns the graph, allowing this to be chained with other functions. Takes O(|E|) time.
# graph.predecessors(v)
Return all nodes that are predecessors of the specified node or undefined if node v is not in the graph. Behavior is undefined for undirected graphs - use neighbors instead. Takes O(|V|) time.
# graph.successors(v)
Return all nodes that are successors of the specified node or undefined if node v is not in the graph. Behavior is undefined for undirected graphs - use neighbors instead. Takes O(|V|) time.
# graph.neighbors(v)
Return all nodes that are predecessors or successors of the specified node or undefined if node v is not in the graph. Takes O(|V|) time.
# graph.inEdges(v, [u])
Return all edges that point to the node v. Optionally filters those edges down to just those coming from node u. Behavior is undefined for undirected graphs - use nodeEdges instead. Returns undefined if node v is not in the graph. Takes O(|E|) time.
# graph.outEdges(v, [w])
Return all edges that are pointed at by node v. Optionally filters those edges down to just those point to w. Behavior is undefined for undirected graphs - use nodeEdges instead. Returns undefined if node v is not in the graph. Takes O(|E|) time.
# graph.nodeEdges(v, [w])
Returns all edges to or from node v regardless of direction. Optionally filters those edges down to just those between nodes v and w regardless of direction. Returns undefined if node v is not in the graph. Takes O(|E|) time.
# graph.parent(v)
Returns the node that is a parent of node v or undefined if node v does not have a parent or is not a member of the graph. Always returns undefined for graphs that are not compound. Takes O(1) time.
# graph.children(v)
Returns all nodes that are children of node v or undefined if node v is not in the graph. Always returns [] for graphs that are not compound. Takes O(|V|) time.
# graph.setParent(v, parent)
Sets the parent for v to parent if it is defined or removes the parent for v if parent is undefined. Throws an error if the graph is not compound. Returns the graph, allowing this to be chained with other functions. Takes O(1) time.
# graph.hasEdge(v, w, [name]) # graph.hasEdge(edgeObj)
Returns true if the graph has an edge between v and w with the optional name. The name parameter is only useful with multigraphs. v and w can be interchanged for undirected graphs. Takes O(1) time.
# graph.edge(v, w, [name]) # graph.edge(edgeObj)
Returns the label for the edge (v, w) if the graph has an edge between v and w with the optional name. Returned undefined if there is no such edge in the graph. The name parameter is only useful with multigraphs. v and w can be interchanged for undirected graphs. Takes O(1) time.
# graph.setEdge(v, w, [label], [name]) # graph.setEdge(edgeObj, [label])
Creates or updates the label for the edge (v, w) with the optionally supplied name. If label is supplied it is set as the value for the edge. If label is not supplied and the edge was created by this call then the default edge label will be assigned. The name parameter is only useful with multigraphs. Returns the graph, allowing this to be chained with other functions. Takes O(1) time.
# graph.removeEdge(v, w)
Removes the edge (v, w) if the graph has an edge between v and w with the optional name. If not this function does nothing. The name parameter is only useful with multigraphs. v and w can be interchanged for undirected graphs. Takes O(1) time.
# json.write(g)
Creates a JSONrepresentation of the graph that can be serialized to a string with JSON.stringify. The graph can later be restored using json-read.
var g = new graphlib.Graph();
g.setNode("a", { label: "node a" });
g.setNode("b", { label: "node b" });
g.setEdge("a", "b", { label: "edge a->b" });
graphlib.json.write(g);
// Returns the object:
//
// {
// "options": {
// "directed": true,
// "multigraph": false,
// "compound": false
// },
// "nodes": [
// { "v": "a", "value": { "label": "node a" } },
// { "v": "b", "value": { "label": "node b" } }
// ],
// "edges": [
// { "v": "a", "w": "b", "value": { "label": "edge a->b" } }
// ]
// }# json.read(json)
Takes JSON as input and returns the graph representation. For example, if we have serialized the graph in json-write to a string named str, we can restore it to a graph as follows:
var g2 = graphlib.json.read(JSON.parse(str));
g2.nodes();
// ['a', 'b']
g2.edges()
// [ { v: 'a', w: 'b' } ]# alg.components(graph)
Finds all connected components in a graph and returns an array of these components. Each component is itself an array that contains the ids of nodes in the component.
Example
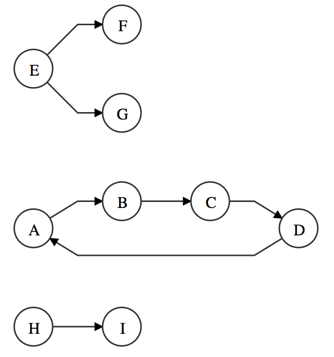
graphlib.alg.components(g);
// => [ [ 'A', 'B', 'C', 'D' ],
// [ 'E', 'F', 'G' ],
// [ 'H', 'I' ] ]# alg.dijkstra(graph, weightFn, edgeFn)
This function is an implementation of Dijkstra's algorithm which finds
the shortest path from source to all other nodes in g. This
function returns a map of v -> { distance, predecessor }. The distance
property holds the sum of the weights from source to v along the
shortest path or Number.POSITIVE_INFINITY if there is no path from
source. The predecessor property can be used to walk the individual
elements of the path from source to v in reverse order.
It takes an optional weightFn(e) which returns the weight of the edge
e. If no weightFn is supplied then each edge is assumed to have a
weight of 1. This function throws an Error if any of the traversed edges
have a negative edge weight.
It takes an optional edgeFn(v) which returns the ids of all edges
incident to the node v for the purposes of shortest path traversal. By
default this function uses the g.outEdges.
It takes O((|E| + |V|) * log |V|) time.
Example:
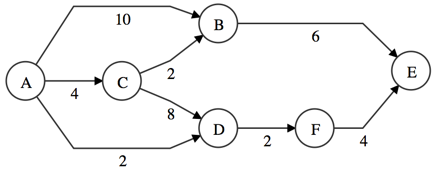
function weight(e) { return g.edge(e); }
graphlib.alg.dijkstra(g, "A", weight);
// => { A: { distance: 0 },
// B: { distance: 6, predecessor: 'C' },
// C: { distance: 4, predecessor: 'A' },
// D: { distance: 2, predecessor: 'A' },
// E: { distance: 8, predecessor: 'F' },
// F: { distance: 4, predecessor: 'D' } }# alg.dijkstraAll(graph, weightFn, edgeFn)
This function finds the shortest path from each node to every other
reachable node in the graph. It is similar to
alg.dijkstra, but instead of returning a single-source
array, it returns a mapping of of source -> alg.dijksta(g, source, weightFn, edgeFn).
This function takes an optional weightFn(e) which returns the
weight of the edge e. If no weightFn is supplied then each edge is
assumed to have a weight of 1. This function throws an Error if any of
the traversed edges have a negative edge weight.
This function takes an optional edgeFn(u) which returns the ids of
all edges incident to the node u for the purposes of shortest path
traversal. By default this function uses g.outEdges.
This function takes O(|V| * (|E| + |V|) * log |V|) time.
Example:

function weight(e) { return g.edge(e); }
graphlib.alg.dijkstraAll(g, function(e) { return g.edge(e); });
// => { A:
// { A: { distance: 0 },
// B: { distance: 6, predecessor: 'C' },
// C: { distance: 4, predecessor: 'A' },
// D: { distance: 2, predecessor: 'A' },
// E: { distance: 8, predecessor: 'F' },
// F: { distance: 4, predecessor: 'D' } },
// B:
// { A: { distance: Infinity },
// B: { distance: 0 },
// C: { distance: Infinity },
// D: { distance: Infinity },
// E: { distance: 6, predecessor: 'B' },
// F: { distance: Infinity } },
// C: { ... },
// D: { ... },
// E: { ... },
// F: { ... } }# alg.findCycles(graph)
Given a Graph, g, this function returns all nodes that
are part of a cycle. As there may be more than one cycle in a graph this
function return an array of these cycles, where each cycle is itself
represented by an array of ids for each node involved in that cycle.
alg.isAcyclic is more efficient if you only need to
determine whether a graph has a cycle or not.
var g = new graphlib.Graph();
g.setNode(1);
g.setNode(2);
g.setNode(3);
g.setEdge(1, 2);
g.setEdge(2, 3);
graphlib.alg.findCycles(g);
// => []
g.setEdge(3, 1);
graphlib.alg.findCycles(g);
// => [ [ '3', '2', '1' ] ]
g.setNode(4);
g.setNode(5);
g.setEdge(4, 5);
g.setEdge(5, 4);
graphlib.alg.findCycles(g);
// => [ [ '3', '2', '1' ], [ '5', '4' ] ]# alg.floydWarshall(graph, weightFn, edgeFn)
This function is an implementation of the Floyd-Warshall algorithm,
which finds the shortest path from each node to every other reachable node
in the graph. It is similar to alg.dijkstraAll, but
it handles negative edge weights and is more efficient for some types of
graphs. This function returns a map of source -> { target -> { distance, predecessor }. The distance property holds the sum of the weights from
source to target along the shortest path of Number.POSITIVE_INFINITY
if there is no path from source. The predecessor property can be used to
walk the individual elements of the path from source to target in
reverse order.
This function takes an optional weightFn(e) which returns the
weight of the edge e. If no weightFunc is supplied then each edge is
assumed to have a weight of 1.
This function takes an optional edgeFn(v) which returns the ids of
all edges incident to the node v for the purposes of shortest path
traversal. By default this function uses the outEdges function on the
supplied graph.
This algorithm takes O(|V|^3) time.
Example:

function weight(e) { return g.edge(e); }
graphlib.alg.floydWarshall(g, function(e) { return g.edge(e); });
// => { A:
// { A: { distance: 0 },
// B: { distance: 6, predecessor: 'C' },
// C: { distance: 4, predecessor: 'A' },
// D: { distance: 2, predecessor: 'A' },
// E: { distance: 8, predecessor: 'F' },
// F: { distance: 4, predecessor: 'D' } },
// B:
// { A: { distance: Infinity },
// B: { distance: 0 },
// C: { distance: Infinity },
// D: { distance: Infinity },
// E: { distance: 6, predecessor: 'B' },
// F: { distance: Infinity } },
// C: { ... },
// D: { ... },
// E: { ... },
// F: { ... } }# alg.isAcyclic(graph)
Given a Graph, g, this function returns true if the
graph has no cycles and returns false if it does. This algorithm returns
as soon as it detects the first cycle. You can use
alg.findCycles to get the actual list of cycles in the
graph.
var g = new graphlib.Graph();
g.setNode(1);
g.setNode(2);
g.setNode(3);
g.setEdge(1, 2);
g.setEdge(2, 3);
graphlib.alg.isAcyclic(g);
// => true
g.setEdge(3, 1);
graphlib.alg.isAcyclic(g);
// => false # alg.postorder(graph, vs)
This function performs a postorder traversal of the graph g starting
at the nodes vs. For each node visited, v, the function callback(v)
is called.
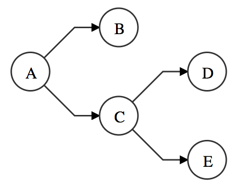
graphlib.alg.postorder(g, "A");
// => One of:
// [ "B", "D", "E", C", "A" ]
// [ "B", "E", "D", C", "A" ]
// [ "D", "E", "C", B", "A" ]
// [ "E", "D", "C", B", "A" ]# alg.preorder(graph, vs)
This function performs a preorder traversal of the graph g starting
at the nodes vs. For each node visited, v, the function callback(v)
is called.

graphlib.alg.preorder(g, "A");
// => One of:
// [ "A", "B", "C", "D", "E" ]
// [ "A", "B", "C", "E", "D" ]
// [ "A", "C", "D", "E", "B" ]
// [ "A", "C", "E", "D", "B" ]# alg.prim(graph, weightFn)
# alg.tarjan(graph)
This function is an implementation of Tarjan's algorithm which finds
all strongly connected components in the directed graph g. Each
strongly connected component is composed of nodes that can reach all other
nodes in the component via directed edges. A strongly connected component
can consist of a single node if that node cannot both reach and be reached
by any other specific node in the graph. Components of more than one node
are guaranteed to have at least one cycle.
This function returns an array of components. Each component is itself an array that contains the ids of all nodes in the component.
Example:
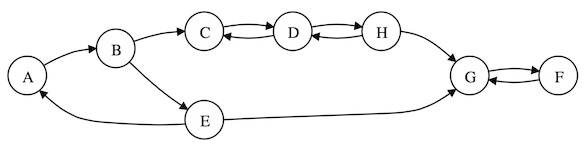
graphlib.alg.tarjan(g);
// => [ [ 'F', 'G' ],
// [ 'H', 'D', 'C' ],
// [ 'E', 'B', 'A' ] ]# alg.topsort(graph)
An implementation of topological sorting.
Given a Graph g this function returns an array of nodes
such that for each edge u -> v, u appears before v in the array. If
the graph has a cycle it is impossible to generate such a list and
CycleException is thrown.
Takes O(|V| + |E|) time.
Example:
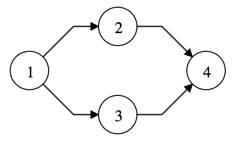
graphlib.alg.topsort(g)
// [ '1', '2', '3', '4' ] or [ '1', '3', '2', '4' ]