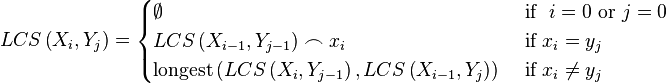Follow up for "Unique Paths":
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
Example
There is one obstacle in the middle of a 3x3 grid as illustrated below.
[
[0,0,0],
[0,1,0],
[0,0,0]
]
The total number of unique paths is 2.
We can use the same approach as Unique Path. We just to set total path to 0 if we meet a obstacle. Note that, it can be accomplish using O(n) extra space for cache.
# assume the grid size is m x n
cache = {0 .. 0} with length of n
for i in 1 .. m
for j in 1 .. n
if obstacleGrid[i][j] = 1 then
cache[j] = 0
else if i = 0 then
if j = 0 then
cache[j] = 1
else
cache[j] = cache[j-1]
else if j != 0 then
cache[j] += cache[j-1]
return the last element in cache
Given a triangle, find the minimum path sum from top to bottom using only O(n) extra space, where n is the total number of rows in the triangle. For each step, it can only move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
It is similar to running sum, we keep tracking all possible sum by doing
It seems to need to require
rows := number of rows in triangle
cache := {MAX_INTEGER} with length = rows
cache[0] := triangle[0][0]
for r in 2 .. rows:
# update cache inplace, so we also need to store
# left parent and right parent of each node
left_parent := cache[0]
# for the left most
cache[0] = left_parent + triangle[r-1][0]
for i in 1 .. r:
right_parent = cache[i]
cache[i] = min(left_parent, right_parent) + triangle[r-1][i]
left_parent = right_parent
return the min number in the cache which is the minimum sum.
Finding the contiguous subarray within a one-dimensional array of numbers (containing at least one positive number) which has the largest sum.
Example
{−2, 1, −3, 4, −1, 2, 1, −5, 4} => {4, -1, 2, 1} = 6
maxSum := -INFINITY
startIndex := 0
endIndex := 0
currentSum := 0
currentStartIndex := 1
for currentEndIndex in 1 .. n
currentSum := currentSum + arr[currentEndIndex]
if currentSum > maxSum then
maxSum := currentSum
startIndex := currentStartIndex
endIndex := currentEndIndex
if currentSum < 0 then
currentSum := 0
currentStartIndex := currentEndIndex + 1
return (maxSum, startIndex, endIndex)
Reference
Maximum subarray problem
Find the contiguous subarray within an array (containing at least one number) which has the largest product.
For example, given the array [2,3,-2,4], the contiguous subarray [2,3] has the largest product = 6.
It is similar to the problem finding maximum sum. However, we could have negative number when it meets an new negative number, the product becomes the maximum. Therefore we need to keep tracking the most negative product or just the minimum product. We also need to take care zeros.
prev_max := arr[1]
prev_min := arr[1]
max_prod := arr[1]
for i in 2 .. arr.length
temp_max := prev_max * arr[i]
temp_min := prev_min * arr[i]
curr_max := max_of_three(prev_max, temp_max, arr[i])
curr_min := min_of_three(prev_min, temp_min, arr[i])
max_prod := max(curr_max, max_prod)
prev_max := curr_max
prev_min := curr_min
return max_prod
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
There are 3 operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
Example
Given word1 = "mart" and word2 = "karma", return 3.
Edit distance refers to Levenshtein distance.
function LevenshteinDistance(word1, word2)
// for all i and j, d[i,j] will hold the Levenshtein distance between
// the first i characters of word1 and the first j characters of word2.
// note that d has (m+1)*(n+1) values
declare matrix d[0..m, 0..n]
set each element in d to zero
// source prefixes can be transformed into empty string by
// dropping all characters
for i from 1 to m
d[i, 0] := i
// target prefixes can be reached from empty source prefix
// by inserting every character
for j from 1 to n
d[0, j] := j
for j from 1 to n
for i from 1 to m
if s[i] = t[j] then
d[i, j] := d[i-1, j-1] // no operation required
else
d[i, j] := minimum(
d[i-1, j] + 1, // a deletion
d[i, j-1] + 1, // an insertion
d[i-1, j-1] + 1) // a substitution
return d[m, n]
Suppose we have a source string with length
The Longest Common Substring can be found using following formular. $$ \mathit{LCSubstr}(S, T) = \max_{1 \leq i \leq m, 1 \leq j \leq n} \mathit{LCSuff}(S_{1..i}, T_{1..j}) ; $$
function LCSubstr(S[1..m], T[1..n])
LCSuffix := matrix(m, n)
# Length of a LCSubstr
max := 0
# Store all LCSubstrs
result := {}
for i := 1..m
for j := 1..n
if S[i] == T[j]
if i == 1 or j == 1
LCSuffix[i,j] := 1
else
LCSuffix[i,j] := LCSuffix[i-1,j-1] + 1
if LCSuffix[i,j] > max
max := LCSuffix[i,j]
result := {S[i-max+1..i]}
else if LCSuffix[i,j] == max
result := result ∪ {S[i-z+1..i]}
else
LCSuffix[i,j] := 0
return result
Given two strings, find the length of longest common subsequence (LCS).
Example
For "ABCD" and "EDCA", the LCS is "A" (or "D", "C"), return 1.
For "ABCD" and "EACB", the LCS is "AC", return 2.
Two observations:
- If two sequences both end in the same element, to find their LCS: shorten each sequence by removing the last element, find the LCS of the shortened sequences, and to that LCS append the removed element.
- If two sequences X and Y do not end in the same symbol. Then the LCS of X and Y is the longer of the two sequences
$$LCS(X_{n},Y_{m-1})$$ and$$LCS(X_{n-1},Y_{m})$$ .
function LCSubseq(S[1..m], T[1..n])
LCSuffix := matrix(m, n)
# Length of a LCSubseq
max_length := 0
for i := 1..m
for j := 1..n
if S[i] == T[j] then
if i == 1 or j == 1 then
LCSuffix[i,j] := 1
else
LCSuffix[i,j] := LCSuffix[i-1,j-1] + 1
else if i != 1 and j != 1 then
LCSuffix[i,j] := max(LCSuffix[i-1,j], LCSuffix[i,j-1])
else
LCSuffix[i,j] := 0
max_length := max(max_length, LCSuffix[i,j])
return max_length
Given a string S and a string T, count the number of distinct subsequences of T in S.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).
Example
Given S = "rabbbit", T = "rabbit", return 3.
Because we only think about sequence, only the order of each character matter. The run-time complexity is O(mn), where w = S.length, n = T.length, since we check each char of S against each char of T, and we use a cache with length equals to length of T. For example:
S = abab, T = ab We start for the first char is S, when we meet an 'a', we set cache[0] += 1 to indicate that we find an new start point. When we meet a 'b', we check for its previous char in T, which is 'a' for its occurrences. So, for the first 'b', 'a' is 1, so set cache[1] = 1. For the second 'b', we have cache[0] = 2, so set cache[1] += cache[0] => 3, because both 'a' can pair with this 'b'.
But there is problem when there are duplicates in T. A char is S can only be used to match a char in T. For exmaple:
S = abbab, T = abb When we meet the first 'b', we can only match it to the first 'b' or second 'b' in T. In other words, after we set cache[1] = 1 (match the first 'b'), we need to used its old value for the second 'b', therefore we set cache[2] = 0 (cache[1] = 0, there is no previous 'b' for the second 'b') instead of 1.
cache := {0 ... 0} with length equals to T.length
for each character as c in S
prev_tmp := 1
for i in 1 .. T.length:
this_tmp := cache[i]
if c = T[i] then
cache[i] += prev_tmp
prev_tmp := this_tmp
return the last value of cache
Given a string s and a dictionary of words dict, determine if s can be break into a space-separated sequence of one or more dictionary words.
Given s = "lintcode", dict = ["lint", "code"].
Return true, because "lintcode" can be break as "lint code".
We can use DP based on following formula.
possible[i] = true if S[0,i] is in the dictionary
= true if possible[k] == true and
S[k+1,i] in the dictionary, 0<k<i
= false if no such k exist.
possible := [False] * s.length
for i in 1 ... s.length
if not possible[i] and s[0:i] in dictionary then
possible[i] = True
if possible[i] then
for k in i+1 ... s.length
if not possible[k] and s[i+1:k] in dictionary then
possible[k] := True
if possible[-1] then
return True
return possible[-1]
Given n items with size
Example
If we have 4 items with size [2, 3, 5, 7], the backpack size is 11, we can select [2, 3, 5], so that the max size we can fill this backpack is 10. If the backpack size is 12. we can select [2, 3, 7] so that we can fulfill the backpack.
The function should return the max size we can fill in the given backpack.
Note
A item can not be divided into small pieces.
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example, Given [10, 9, 2, 5, 3, 7, 101, 18], The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.
By storing the longest subsequence length ending at
for
P[i] = j
Could you improve it to O(n log n) time complexity?