线性方程组是线性代数的核心部分。 许多问题可以表述为线性方程组,而线性代数为我们提供了解决它们的工具。
例 2.1
公司生产的产品 $ N_1,...,N_n $ 需要原材料 $ R_1,...,R_m $。为了生产一个单位的产品 $ N_j $,需要 $ a_{ij} $ 个单位的资源 $ R_i $,其中 $ i = 1,...,m $ 且 $ j = 1,...,n $。目标是找到一个最佳生产计划,即如果总共有 $ b_i $ 个单位的资源 $ R_i $ 可用并且(理想情况下)没有剩余资源,则应该生产多少单位 $ x_j $ 的产品 $ N_j $。 如果我们生产 $ x_1,...,x_n $ 个单位对应的产品,我们一共需要 $$ a_{i1}x_1 + \cdots + a_{in}x_n \tag{2.2} $$ 个单位的资源 $ R_i $。因此,最优生产计划 $ (x_1,...,x_n) \in \mathbb{R}^n $ 必须满足以下方程组: $$ \begin{array}{clr} a_{11}x_1 + \cdots + a_{1n}x_n & = b_1 \ & \vdots \ a_{m1}x_1 + \cdots + a_{mn}x_n & = b_m \tag{2.3} \end{array} $$ 其中 $ a_{ij} \in \mathbb{R} $ 和 $ b_i \in \mathbb{R} $。
方程(2.3)是线性方程组(system of linear equations)的一般形式,$ x_1,...,x_n $ 是这个系统的未知数。 满足(2.3)的每一个n元组 $ (x_1,...,x_n) \in \mathbb{R}^n$ 都是线性方程组的一个解。
例 2.2
线性方程组: $$ \begin{array}{clr} x_1 + x_2 + x_3 & = 3 &(1)\ x_1 - x_2 + 2x_3 & = 2 &(2)\ 2x_1 + 3x_3 & = 1 &(3) \tag{2.4} \end{array} $$ 没有解 :将前两个方程相加得到 $ 2x_1 + 3x_3 = 5 $ ,这与第三个方程相矛盾。 让我们看看线性方程组 $$ \begin{array}{clr} x_1 + x_2 + x_3 & = 3 &(1)\ x_1 - x_2 + 2x_3 & = 2 &(2)\ x_2 + x_3 & = 2 &(3)\tag{2.5} \end{array} $$ 从第一个和第三个等式可以得出 $ x_1 = 1 $ 。 从(1)+(2),我们得到 $ 2x_1 + 3x_3 = 5 $,即 $ x_3 = 1 $。从 (3) 中,我们得到 $ x_2 = 1 $。 因此,(1,1,1) 是唯一可能且 唯一的解(通过插入验证(1,1,1)是解)。 作为第三个例子,我们考虑 $$ \begin{array}{clr} x_1 + x_2 + x_3 & = 3 &(1)\ x_1 - x_2 + 2x_3 & = 2 &(2)\ 2x_1 + 3x_3 & = 5 &(3)\tag{2.6} \end{array} $$ 由于(1)+(2)=(3),我们可以省略第三个方程(冗余)。 从(1)和(2),我们得到 $ 2x_1 = 5 - 3x_3 $ 和 $ 2x_2 = 1 + x_3 $。 我们定义 $ x_3 = a \in \mathbb{R} $ 作为一个自由变量,使得任何三元组 $$ \left( \frac{5}{2} - \frac{3}{2}a, \frac{1}{2} + \frac{1}{2}a, a \right), a \in \mathbb{R} \tag{2.7} $$ 都是线性方程组的解,即我们得到一个包含无限多个解的解集。
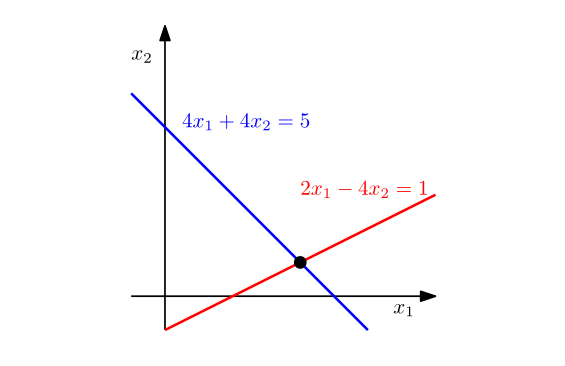
图 2.3 具有两个变量的两个线性方程组的解空间可以在几何上解释为两条线的交点。 每个线性方程代表一条线。
一般而言,对于实值线性方程组,我们要么没有,只有一个,要么有无穷多个解。 当我们无法求解线性方程组时,线性回归(第9章)是解决例2.1的一个版本。
备注 (线性方程组的几何解释)。 在具有两个变量 $ x_1, x_2 $ 的线性方程组中,每个线性方程定义 $ x_1 x_2 $ 平面上的一条线。 由于线性方程组的解必须同时满足所有方程,因此解集是这些线的交点。 该交集可以是一条线(如果线性方程描述同一条线)、一个点或空(当这些线平行时)。 图 2.3 给出了方程组 $$ \begin{array}{clr} 4x_1 + 4x_2 & = 5 \ 2x_1 - 4x_2 & = 1 \tag{2.8} \end{array} $$ 的说明,其中解空间是点 $ (x_1, x_2) = (1, \frac{1}{4}) $。 类似地,对于三个变量,每个线性方程确定三维空间中的一个平面。 当我们与这些平面相交时,即同时满足所有线性方程,我们可以得到一个解集,它是一个平面、一条线、一个点或空的(当这些平面没有公共交点时)。
对于求解线性方程组的系统方法,我们将引入一个有用的紧凑符号。 我们将系数 $ a_{ij} $ 收集到向量中并将向量收集到矩阵中。 换句话说,我们按照以下形式编写(2.3)中的系统: $$ \begin{bmatrix} a_{11} \ \vdots \ a_{m1} \end{bmatrix}x_1 + \begin{bmatrix} a_{12} \ \vdots \ a_{m2} \end{bmatrix}x_2 + \cdots + \begin{bmatrix} a_{1n} \ \vdots \ a_{mn} \end{bmatrix}x_n = \begin{bmatrix} b_1 \ \vdots \ b_m \end{bmatrix} \tag{2.9} $$ $$ \Longleftrightarrow \begin{bmatrix} a_{11} & \cdots & a_{1n} \ \vdots \ a_{m1} & \cdots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1 \ \vdots \ x_n \end{bmatrix} = \begin{bmatrix} b_1 \ \vdots \ b_m \end{bmatrix} \tag{2.10} $$
下面,我们将仔细研究这些矩阵并定义计算规则。 我们将在2.3节返回求解线性方程。