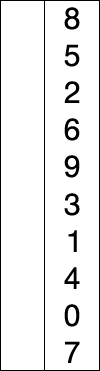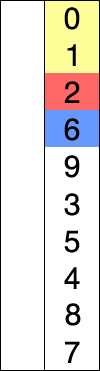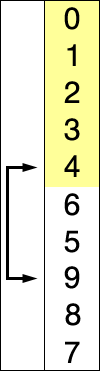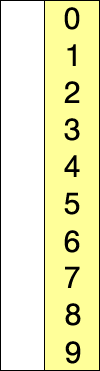
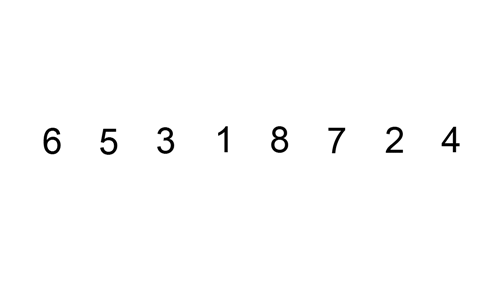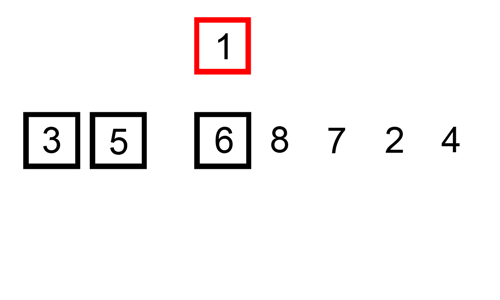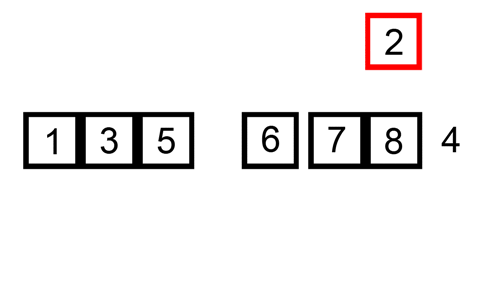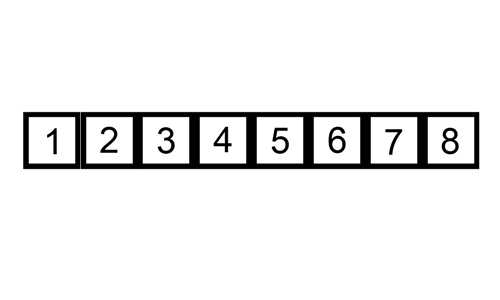Skip to content

Latest commit

 

History

History
518 lines (457 loc) · 22.9 KB

README.MD

File metadata and controls

518 lines (457 loc) · 22.9 KB

排序

插入排序

交换排序

选择排序

归并排序

基数排序

总结

插入排序

基本思想：每一趟将一个待排序的记录，按其关键字的大小插入到已排好序的一组记录的适当位置上，直到所有待排序记录全部插入为止。

直接插入排序(straight Insertion sort)

核心：通过构建有序序列，对于未排序序列，在已排序序列中从后向前扫描(对于单向链表则只能从前往后遍历)，找到相应位置并插入。

  • 从第一个元素开始，该元素可认为已排序
  • 取下一个元素，对已排序数组从后往前扫描
  • 若从排序数组中取出的元素大于新元素，则移至下一位置
  • 重复步骤3，直至找到已排序元素小于或等于新元素的位置
  • 插入新元素至该位置
  • 重复2~5

insertion_sort.gif

代码实现

#include <iostream>
using namespace std;
int main(){
	int a[] = {-1, 6, 5, 2, 8, 4, 1, 3, 7}; //数组从第二位开始,第一位[0]为暂存单元
	int len = sizeof(a) / sizeof(a[0]);
	for(int i = 2; i < len; i++){
		if(a[i] < a[i - 1]){
			a[0] = a[i];
			a[i] = a[i - 1];
			int j = i - 2;
			while(a[0] < a[j]){
				a[j + 1] = a[j];
				j--;
			}
			a[j + 1 ] = a[0];
		}
	}
	for(int i = 1; i < len; i++)
		cout << a[i];
	return 0;
}

算法分析

  • 空间复杂度：需要一个记录的辅助空间[0],空间复杂度为 O(1).
  • 时间复杂度：一共操作了 n-1 趟，每趟都分为比较和移动两部分。最好情况，只比较不移动，O(n);最坏情况，比较 n2/2 次，移动 n2/2 次， 时间复杂度为O(n2).

算法特点

  • 稳定排序。
  • 也适合于链式存储，只需修改相应的指针，无需移动。
  • 适合于初始记录基本有序(正序)的情况，当初始记录无序，n较大时，此算法时间复杂度较高，不宜使用。

折半插入排序(Binary Insertion Sort)

直接插入排序每一趟都需要在排好序的部分中从最后一位开始比较。折半插入排序减少了比较的次数，但移动次数没有改变。

代码实现

#include <iostream>
using namespace std;
int main(){
	int a[] = {-1, 6, 5, 2, 8, 4, 1, 3, 7}; //数组从第二位开始, 第一位[0]为暂存单元
	int len = sizeof(a) / sizeof(a[0]);
	for(int i = 2; i < len; i++){
		a[0] = a[i];
		int low = 1, high = i - 1;
		while(low <= high){
			int m = (low + high) / 2;
			if(a[0] < a[m]) high = m - 1;
			else low = m + 1;
		}
		for(int j = i - 1; j >= high + 1; j--)
			a[j + 1] = a[j];
		a[high + 1] = a[0];
	}
	for(int i = 1; i < len; i++)
		cout << a[i];
	return 0;
}

算法分析

  • 时间复杂度：移动次数没有变，所以时间复杂度还是 O(n2).
  • 空间复杂度：O(1).

算法特点

  • 稳定排序。
  • 只能用于顺序结构，不能用于链式结构。
  • 适合初始记录无序、n较大时的情况。

希尔排序(Shell's Sort)

直接插入排序，当待排序的记录个数较少且待排序序列的关键字基本有序时，效率较高。希尔排序针对以上两个方面进行了改进。 希尔排序实现上是将待排序序列分成几组分别进行插入排序，最后再合成一组。

基本思想: 先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量 =1，即所有记录放在同一组中进行直接插入排序为止。 一般的初次取序列的一半为增量，以后每次减半，直到增量为1。

代码实现

#include <iostream>
using namespace std;
int main(){
	int a[] = {6, 5, 2, 8, 4, 1, 3, 7};
	int len = sizeof(a) / sizeof(a[0]);
	int step = len / 2;  //初次增量为len/2
	while(step > 0){
		for(int i = step; i < len; i += step){
			while(i >= step && a[i - step] > a[i]){
				int temp = a[i - step];
				a[i - step] = a[i];
				a[i] = temp;
				i -= step;
			}
		}
		step = step / 2;
	}
	for(int i = 0; i < len; i++)
		cout << a[i];
	return 0;
}

算法分析：

  • 时间复杂度：最坏情况 O(n2)
  • 空间复杂度：只需要一个辅助空间，O(1).

算法特点:

  • 不稳定排序。
  • 只能用于顺序结构。
  • 记录总的比较次数和移动次数都比直接插入排序要少，n越大时，效果越明显。适合初始记录无序、较大时的情况。

交换排序

交换排序的基本思想是：两两比较待排序记录的关键字，一旦发现两个记录不满足次序要求时则进行交换，直到整个序列全部满足要求为止。

冒泡排序(Bubble Sort)

核心：冒泡，持续比较相邻元素，大的挪到后面，因此大的会逐步往后挪，故称之为冒泡。
每一次循环将未排序数组中最大的移到最后，所以下一次循环可以只比较到前一位

BubbleSort

算法实现

#include <iostream>
using namespace std;
int main(){
	int a[] = {6, 5, 2, 8, 4, 1, 3, 7};
	int len = sizeof(a) / sizeof(a[0]);
	int m = len - 1, flag = 1;
	while((m > 0) && (flag == 1)){
		flag = 0;
		for(int i = 1; i <= m; i++){
			if(a[i - 1] > a[i]){
				flag = 1;
				int temp = a[i - 1];
				a[i - 1] = a[i];
				a[i] = temp;
			}
		}
		m--;
	}
	for(int i = 0; i < len; i++)
		cout << a[i];
	return 0;
}

算法分析

  • 时间复杂度： 最好情况下只进行 n-1 次比较； 最坏情况下，进行 n(n-1)/2 次比较，移动 3n(n-1)/2次。时间复杂度为 O(n2).
  • 空间复杂度： 只需要一个暂存空间， O(1).

算法特点

  • 稳定排序
  • 可用于链式存储
  • 移动次数较多，算法平均时间性能比直接插入排序差。当初始记录无序，n较大时，不宜采用.

快速排序(Quick Sort)

可以参考这篇文章。另外，我总结的是按照严蔚敏教材的内容，所以与那篇文章有所不同，不过思想是一样的。

快速排序是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

【算法步骤】

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为枢纽(或支点)，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，结果将待排序记录分成两个子表，枢纽处于最终位置。然后分别对左右子表重复上述过程，直到每一个子表只有一个记录时，排序完成。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

【具体步骤】

  • 选择待排序表中的第一个记录作为枢纽，将枢纽记录暂存在r[0]的位置上。附设两个指针low和high，初始时分别指向表的下界和上届(第一趟时，low=1;high=length-1;)。
  • 从表的最右侧位置依次向左搜索，找到第一个小于关键字pivotkey的记录，将其移到low处。(当low<high时，若 r[high]>=pivotkey , high--; 若 r[high]<pivotkey, r[low]=r[high];)
  • 然后再从左依次向右搜索第一个大于privotkey的记录，将其移到此时的high处。
  • 重复2和3，直到low==high位置，此时low==high这个位置就是pivotkey(即此时的r[0])的最终位置，原表被分为两个子表。
  • 分别对左右表执行以上操作。(递归).

代码实现

#include <iostream>
using namespace std;
void quickSort(int list[], int low, int high)
{
	if(low < high){
		list[0] = list[low];
		int key = list[low];
		int left = low, right = high;
		while(low < high){
			while(low < high && list[high] >= key) high--;
			list[low] = list[high];
			while(low < high && list[low] <= key) low++;
			list[high] = list[low];
		}
		list[low] = list[0];
		quickSort(list,left,low-1);
		quickSort(list, low+1, right);
	}
}
int main(){
	int a[] = {-1, 6, 5, 2, 8, 4, 1, 3, 7};
	int len = sizeof(a) / sizeof(a[0]);
	quickSort(a, 1, len - 1);
	for(int i = 1; i < len; i++)
		cout << a[i];
	return 0;
}

【算法分析】

  • 空间复杂度：快速排序是递归的，执行时需要一个栈来存放相应数据。最大递归次数与递归树的深度一致，所以最好情况下的空间复杂度为 O(log2n)，最坏情况下为 O(n).
  • 时间复杂度：最好情况：每一趟排序后都能将序列均匀分割成两个长度大致相等的子表，类似折半查。此时时间复杂度为 O(nlog2n)。最坏情况为待排序列基本有序，每次只能划分比上一次少一个的子序列。平均时间复杂度为 O(nlog2n)。

【算法特点】

  • 不稳定排序。
  • 需要两个位置指针，很难用于链式结构。
  • 当n较大时，在平均情况下快速排序时内部排序方法中速度最快的一种，所以适合初始记录无序、n较大时的情况。

选择排序

选择排序的基本思想是：每一趟从待排序的记录中选出关键字最小的记录，按顺序放在已排序的记录序列的最后，直到排完为止。

简单选择排序(Simple Selection Sort)

核心： 每一趟在未排序序列中选择最小的记录放到已排序序列的最后。

【算法步骤】

  • 第一趟从r[1]开始，从待排序序列[r[1]...r[n]]中找到最小的记录r[k]，交换r[1]和r[k]。
  • 第二趟从r[2]开始，通过n-2次查找，从 n-1 个记录中找到最小的r[k]，交换r[2]和r[k]。
  • 依次类推，经过 n-1 趟， 排序完成。

selection_sort.gif

代码实现

#include <iostream>
using namespace std;
int main(){
	int a[] = {-1, 6, 5, 2, 8, 4, 1, 3, 7};  //为了和教材一致，数组从第1位开始
	int len = sizeof(a) / sizeof(a[0]);
	for(int i = 1; i < len; i++){   
		int k = i;
		for(int j = i + 1; j < len; j++){
			if(a[j] < a[k]) k = j;
		}
		if(k != i){
			int temp = a[i];
			a[i] = a[k];
			a[k] = temp;
		}
	}
	for(int i = 1; i < len; i++)
		cout << a[i];
	return 0;
}

【算法分析】

  • 空间复杂度: O(1).
  • 时间复杂度: 简单排序所需移动次数较少。最好情况（正序），不移动，最坏情况（逆序），移动 3(n-1) 次。 无论初始排列如何，所需进行比较的次数相同，均为 n2/2次。

【算法特点】

  • 稳定性：就选择排序方法本身来讲，它是一种稳定的排序方法。但某些情况下，如 a[]=[2,2,1],第一趟，a[0]与a[2]交换，两个2 a[0] 与a[1]的相对位置发生改变，这是因为采用“交换记录”的策略所造成的，改变这个策略，可以写出不产生这种不稳定现象的选择排序算法。
  • 可用于链式存储结构。
  • 移动记录次数较少，当每一记录占用的空间较多时，此方法比直接插入排序快。

堆排序(Heap Sort)

先参考这篇文章

堆排序是一种树形选择排序，在排序过程中，将待排序的记录r[1..n]看成是一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序的序列中选择关键字最大（或最小）的记录。

Heapsort-example.gif

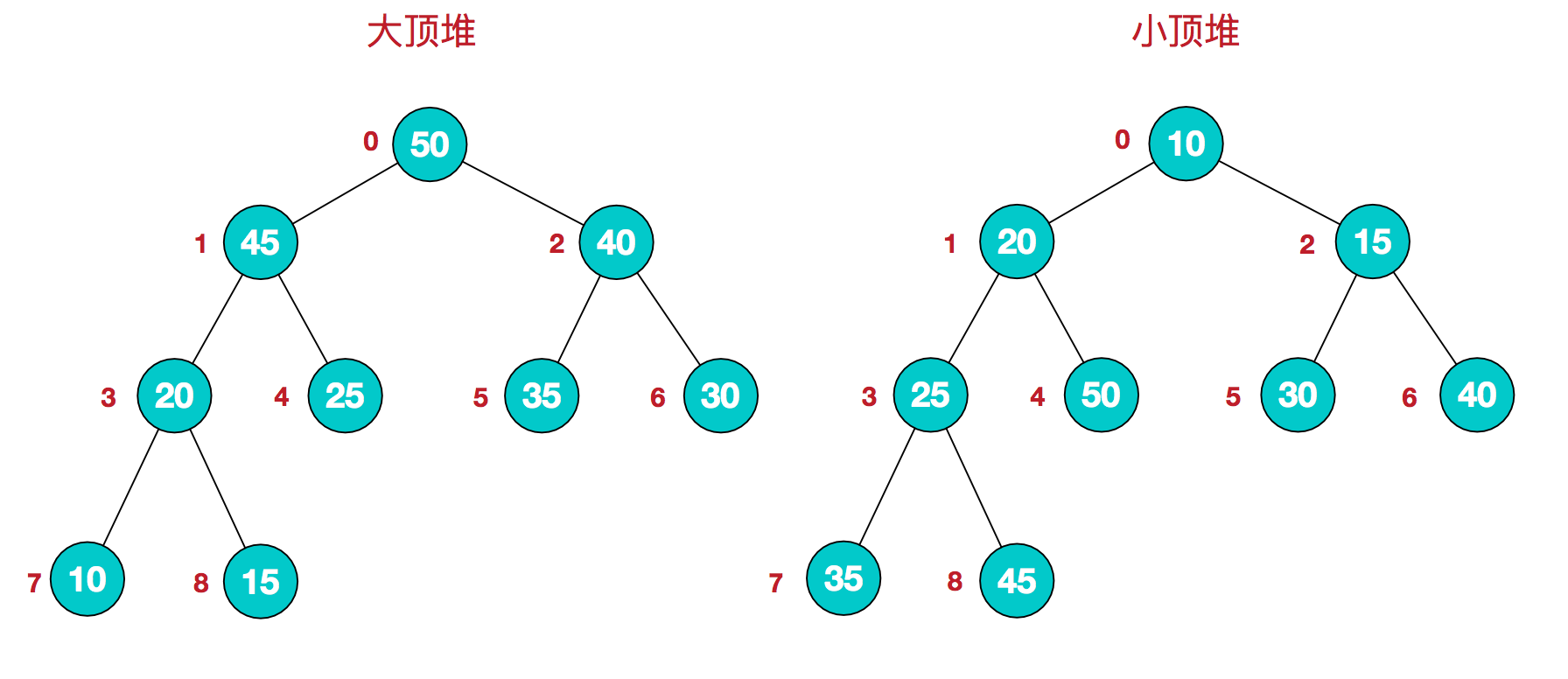
　　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

dui.png

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子 (图中编号从0开始，教材中从1开始）

dui1.png

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

(图中编号从0开始，教材中从1开始）

大顶堆：arr[i] >= arr[2i] && arr[i] >= arr[2i+1]

小顶堆：arr[i] <= arr[2i] && arr[i] <= arr[2i+1]

堆经常被用来实现优先级队列 优先级队列在操作系统的作业调度和其他领域有广泛的应用。

堆排序的关键是__构造初始堆__,对初始序列建堆，就是一个反复筛选的过程。n个结点的完全二叉树，最后一个结点是第[n/2]个结点的孩子。对第[n/2]个结点为根的子树筛选（对于大根堆：若根结点的关键字小于子女中关键字较大者，则交换），使该子树成为堆。之后向前依次对各节点为根的子树进行筛选，看该结点值是否大于其左右子结点的值，若不是，将左右子结点中较大值与之交换，交换后可能会破坏下一级的堆，于是继续采用上述方法构造下一级的堆，直到以该结点为根的子树构成堆为止。反复利用上述调整堆的方法建堆，直到根结点。

【调整堆算法步骤】（教材中编号从1开始）

  • 从r[2s]和r[2s+1]中选出关键字较大者，假设r[2s]的关键字较大，比较r[s]和r[2s]的关键字（就是选出这棵子树的最大值）
  • 交换。将三者最大值交换到子树根结点位置，即r[s]处。（若 r[s]>=r[2s],不需调整；若r[s]<r[2s],交换两者位置。）
  • 递归调用，直到根结点，即到r[1]处。

算法实现

void adjust(int arr[], int len, int index)
{
	int left = 2 * index ;     //下标从0开始的话改为 2 * index + 1
	int right = 2 * index + 1; //下标从0开始的话改为 2 * index + 2
	int maxIdx = index;
	if(left < len && arr[left] > arr[maxIdx]) maxIdx = left;
	if(right < len && arr[right] > arr[maxIdx]) maxIdx = right;
	if(maxIdx != index)
	{
		int temp = arr[maxIdx];
		arr[maxIdx] = arr[index];
		arr[index] = temp;
		adjust(arr, len, maxIdx);
	}
}

调整堆后就是建初堆，也就是将以每一个结点为根的子树都调整为堆。 __就是从[n/2]开始调用调整堆，直到[n/2]-1、...、[1] __ 然后将堆顶元素，就是最大的元素放到序列最后，继续调整剩余的元素，循环

算法实现

void heapSort(int arr[], int size)
{
	for(int i = size / 2 ; i >= 1; i--)   //下标从0开始的话改为 size / 2 - 1; i >= 0;
		adjust(arr, size, i);
	for(int i = size - 1; i >= 1; i--)
	{
		int tmp = arr[1];   // 下标从0开始的话改为 arr[0]
		arr[1] = arr[i];
		arr[i] = tmp;
		adjust(arr, i, 1);
	}
}

完整代码 (下标从1开始）

#include <iostream>
using namespace std;

void adjust(int arr[], int len, int index)
{
	int left = 2 * index ;     //下标从0开始的话改为 2 * index + 1
	int right = 2 * index + 1; //下标从0开始的话改为 2 * index + 2
	int maxIdx = index;
	if(left < len && arr[left] > arr[maxIdx]) maxIdx = left;
	if(right < len && arr[right] > arr[maxIdx]) maxIdx = right;
	if(maxIdx != index)
	{
		int temp = arr[maxIdx];
		arr[maxIdx] = arr[index];
		arr[index] = temp;
		adjust(arr, len, maxIdx);
	}
}
void heapSort(int arr[], int size)
{
	for(int i = size / 2 ; i >= 1; i--)   //下标从0开始的话改为 size / 2 - 1; i >= 0;
		adjust(arr, size, i);
	for(int i = size - 1; i >= 1; i--)
	{
		int tmp = arr[1];   // 下标从0开始的话改为 arr[0]
		arr[1] = arr[i];
		arr[i] = tmp;
		adjust(arr, i, 1);
	}
}

int main(){
	int a[] = {-1, 6, 5, 2, 8, 4, 1, 3, 7}; 
	int len = sizeof(a) / sizeof(a[0]);
	heapSort(a, len);
	for(int i = 0; i < len; i++)
		cout << a[i];
	return 0;
}

【算法分析】

  • 空间复杂度： 仅需一个供交换用的辅助空间，空间复杂度为 O(1)。
  • 时间复杂度： 运行时间主要耗费在建初堆和调整堆时的反复筛选上。 时间复杂度为 O(nlog2n)。

【算法特点】

  • 是不稳定排序。
  • 只能用于顺序结构。
  • 初始堆所需的比较次数较多，因此记录数较少时不宜使用。堆排序在最坏情况下时间复杂度为 O(nlog2n)， 相对于快速排序最坏情况下的 O(n2)而言是一个优点，当记录较多时较为高效。

归并排序(Merging Sort)

归并排序就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并称为2-路合并，2-路合并最为简单和常用。
核心：将两个有序对数组归并成一个更大的有序数组。通常做法为递归排序，并将两个不同的有序数组归并到第三个数组中。

先来看看动图，归并排序是一种典型的分治应用。

merge_sort.gif

假设初始序列有n个记录，则可看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到 n/2 个长度为2或1的有序子序列；再两两归并，...,直到得到一个长度为n的有序子序列为止。

【算法步骤】

  • 将当前序列一分为二，求出分裂点 mid=(low+high)/2;
  • 对子序列R[low...mid]递归，进行归并排序，结果放入S[low...mid]中；
  • 对子序列R[mid+1...high]递归，进行归并排序，结果放入S[mid+1...high]中；
  • 将两个子序列归并为一个有序的序列.

算法实现

#include <iostream>
using namespace std;
//合并左右子表
void Merge(int arr[], int left, int mid, int right)
{
	int *temp = new int[right - left];
	int t = 0;
	int i = left;
	int j = mid;
	while(i < mid && j < right){
		if(arr[i] <= arr[j]) temp[t++] = arr[i++];
		else temp[t++] = arr[j++];
	}
	while(i < mid) temp[t++] = arr[i++];
	while(j < right) temp[t++] = arr[j++];
	t = 0;
	for(int i = left; i < right; i++)
		arr[i] = temp[t++];
	delete[] temp;
}
//归并排序
void MSort(int arr[], int left, int right)
{
	if(left + 1 < right){
		int mid = (left + right) / 2;
		MSort(arr, left, mid);
		MSort(arr, mid, right);
		Merge(arr, left, mid, right);
	}
}

int main(){
	int a[] = {6, 5, 2, 8, 4, 1, 3, 7};
	int len = sizeof(a) / sizeof(a[0]);
	MSort(a, 0 , len);
	for(int i = 0; i < len; i++)
		cout << a[i];
	return 0;
}

【算法分析】

  • 空间复杂度：需要 n 个辅助空间， O(n)。
  • 时间复杂度：当有n各记录时，需进行[log2n]趟归并排序，每一趟归并，其关键字比较次数不超过n，元素移动次数都是n，因此，归并排序的时间复杂度为 O(nlog2n)。

【算法特点】

  • 是稳定排序。
  • 可用于链式结构，且不需要附加存储空间，但递归实现时仍需要开辟相应的递归工作栈。

基数排序(Radix Sorting)

基数排序不是基于比较进行排序的，而是根据关键字各位的值，通过对待排序记录进行若干趟“分配”与“收集”来实现排序的，是一种借助于多关键字排序的思想对单关键字排序的方法。

【算法分析】

  • 时间复杂度：对于n个记录（假设每个记录含d个关键字，每个关键字的取值范围为rd个值）进行链式基数排序时，每一趟分配的时间复杂度为O(n)， 每一趟收集的时间复杂度为O(rd),整个排序需进行d趟分配和收集，所以时间复杂度为O(n+rd))。
  • 空间复杂度：所需辅助空间为2rd个队列指针，另外由于需用链表做存储结构，则相对于其他以顺序结构存储记录的排序而言，还增加了n个指针域空间，所以时间复杂度为O(n+rd)。

【算法特点】

  • 是稳定排序。
  • 可用于链式结构，也可用于顺序结构。
  • 时间复杂度可以突破基于关键字比较一类方法的下界 O(nlog2n),达到 O(n)。
  • 基数排序使用条件有严格的要求：需要知道各级关键字的主次关系和各级关键字的取值范围。

总结

排序分为内部排序和外部排序，内部排序是外部排序的基础，必须通过内部排序产生初始归并段之后，才能进行外部排序。 各种内部排序方法的比较

排序方法 最好情况 最坏情况 平均情况 空间复杂度 稳定性
直接插入排序 O(n) O(n2) O(n2) O(1) 稳定
折半插入排序 O(nlog2n) O(n2) O(n2) O(1) 稳定
希尔排序 O(n1.3) O(1) 不稳定
冒泡排序 O(n) O(n2) O(n2) O(1) 稳定
简单选择排序 O(n2) O(n2) O(n2) O(1) 稳定
快速排序 O(nlog2n) O(n2) O(nlog2n) O(log2n) 不稳定
堆排序 O(nlog2n) O(nlog2n) O(nlog2n) O(1) 不稳定
归并排序 O(nlog2n) O(nlog2n) O(nlog2n) O(n) 稳定
基数排序 O(d(n + rd)) O(d(n + rd)) O(d(n + rd)) O(n + rd) 稳定

从表中平均情况可以看到，直接插入、折半插入、冒泡排序和简单选择排序速度较慢。从算法实现的角度来看，速度较慢的算法实现过程比较简单，称之为简单的排序方法；而速度较快的算法可以看作是对某一算法的改进，称之为先进的排序算法，但这些算法实现过程比较复杂。在使用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。一般综合考虑以下因素：

  • 待排序的记录个数。
  • 记录本身的大小。
  • 关键字的结构和初始状态。
  • 对排序稳定性的要求
  • 存储结构。

有以下结论：

  1. 当n较小，初始记录基本有序，可选用直接插入排序或冒泡排序。
  2. n较大时，当关键字分布随机，稳定性不做要求，可采用快速排序；当关键字基本有序，稳定性不做要求，可采用堆排序；当关键字基本有序，内存允许且要求排序稳定时，可采用归并排序。
  3. 可以将不同排序算法结合使用。如n较大时，可以先将待排序序列划分成若干子序列，分别进行直接插入排序，然后再利用归并排序，将有序子序列合并成一个完整的有序序列。
  4. 折半插入排序、希尔排序、快速排序和堆排序不能用于链式存储。