Skip to content

Latest commit

 

History

History
127 lines (81 loc) · 6.05 KB

README.md

File metadata and controls

127 lines (81 loc) · 6.05 KB
Raw

Miniball

A C++ and Java library to compute the miniball (a.k.a. min-circle, min-sphere, smallest enclosing sphere, etc.) of a point set.

The code works for points in arbitrary dimension. It runs very fast in low dimensions and is practically efficient up to dimensions 10,000. The implementation is based on the algorithm from the paper "Fast Smallest-Enclosing-Ball Computation in High Dimensions" by Kaspar Fischer, Bernd Gärtner, and Martin Kutz (Proc. 11th European Symposium on Algorithms (ESA), p. 630-641, 2003).

This project is dedicated to Martin Kutz†.

Speed

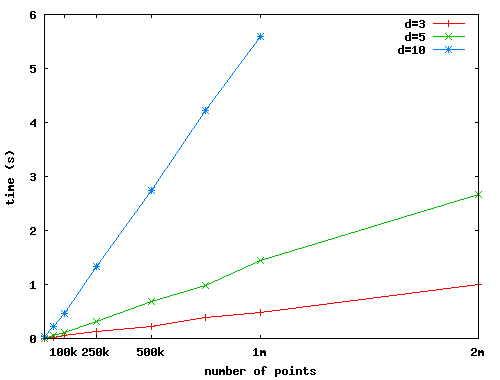
On a 2.66 GHz Intel Core i7 MacBook Pro, the code performs as follows:

The chart shows the time in seconds (y-axis) needed for the computation of the miniball of n random points (x-axis) in dimensions d (3, 5, or 10 in this chart).

Stability

The code is well-tested and its underlying algorithm should be numerically stable. By "numerically stable" we mean that even for points in degenerate position – like all on a line, all on a circle, identical points in the input, etc. – the algorithm will (i) terminate, (ii) be fast, (iii) provide an accurate result.

Please report any problems you may find as tickets.

Getting started (Java)

You can either download the latest JAR file from TODO or use a build system like Maven or Graddle, or SBT (for Scala users).

Maven dependency:

<dependency>
  <groupId>com.dreizak</groupId>
  <artifactId>miniball</artifactId>
  <version>1.0.1</version>
</dependency>

SBT dependency:

libraryDependencies += "com.dreizak" % "miniball" % "1.0.3"

Documentation:

Getting started (C++)

On Linux or MacOS, the following steps will get you going: (Notice that the Boost library that the instructions below download is only used in this example to generate some input points; the library as such does not depend on it.)

# Get the source code
git clone https://github.com/hbf/miniball.git
cd miniball/cpp/test

# Compile an example, which generates random points and computes their miniball
g++ -I../main example.C -o example -O3

# Run it on one million points in 3D
./example 1000000 3

(More documentation to come. Contact us in case you run into any problems.)

Getting started (Python)

On MacOS, do the following (not yet made on other ).

  1. Stand in the python-folder.
  2. Run pip install setup.py (you may need to use the --user option or sudo).
  3. Run pytest (if you do not have it, install it through pip install pytest) to see that it works and that all tests pass.
  4. Does it work? Great! You are now ready to use the python function.

Getting started (C#)

On Linux or MacOS, the following steps will get you going:

# Get the source code
git clone https://github.com/hbf/miniball.git
cd miniball/csharp

# Compile an example, which generates random points and computes their miniball
dotnet build

# Run it on one million points in 3D
./example/bin/Debug/net7.0/example 1000000 3

To run unit tests:

dotnet test

Float or double?

The C++ code is written using templates and allows the number type to be specified as a template argument.

However, please only use double as the number type, as is illustrated in the example program example.C (see line typedef double FT).

The code will not run correctly if you use float.

License

The code is available under the Apache 2 License, which is explained [here](http://www.tldrlegal.com/license/apache-license-2.0-(apache-2.0).

If you use the code in your project/product, please drop us a note – we are always interested in learning about new applications!

Authors & acknowledgements

Authors:

Many thanks go to the following people who have – sometimes substantially – contributed to the code:

Links