参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
这周我们正式开始讲解背包问题!
背包问题的经典资料当然是:背包九讲。在公众号「代码随想录」后台回复:背包九讲,就可以获得背包九讲的pdf。
但说实话,背包九讲对于小白来说确实不太友好,看起来还是有点费劲的,而且都是伪代码理解起来也吃力。
对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包。
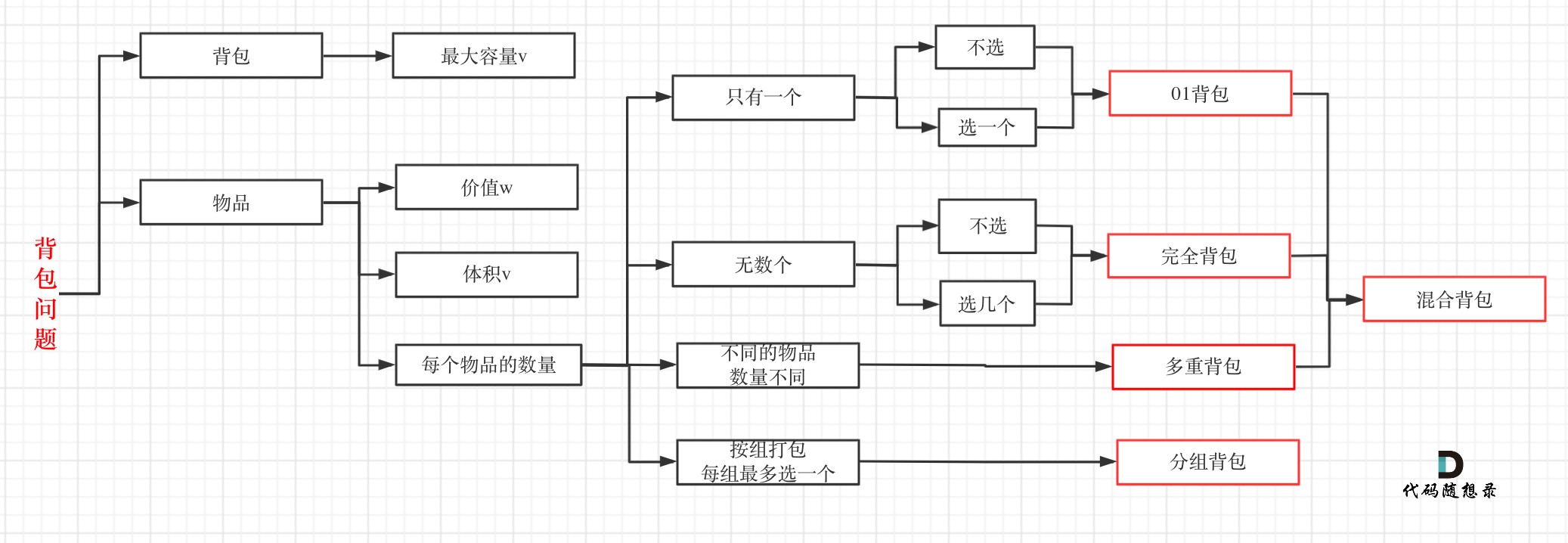
如果这几种背包,分不清,我这里画了一个图,如下:
至于背包九讲其其他背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
而完全背包又是也是01背包稍作变化而来,即:完全背包的物品数量是无限的。
所以背包问题的理论基础重中之重是01背包,一定要理解透!
leetcode上没有纯01背包的问题,都是01背包应用方面的题目,也就是需要转化为01背包问题。
所以我先通过纯01背包问题,把01背包原理讲清楚,后续再讲解leetcode题目的时候,重点就是讲解如何转化为01背包问题了。
之前可能有些录友已经可以熟练写出背包了,但只要把这个文章仔细看完,相信你会意外收获!
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
这是标准的背包问题,以至于很多同学看了这个自然就会想到背包,甚至都不知道暴力的解法应该怎么解了。
这样其实是没有从底向上去思考,而是习惯性想到了背包,那么暴力的解法应该是怎么样的呢?
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是$o(2^n)$,这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
在下面的讲解中,我举一个例子:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
以下讲解和图示中出现的数字都是以这个例子为例。
依然动规五部曲分析一波。
- 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
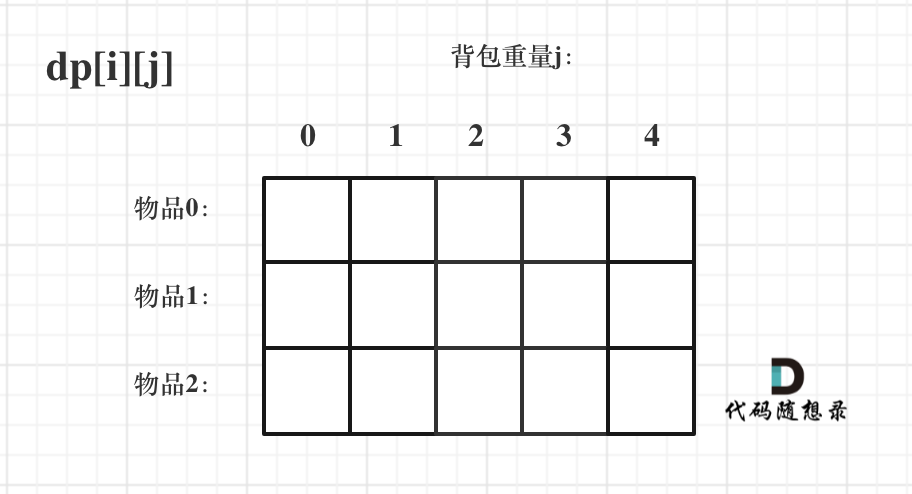
只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
- 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
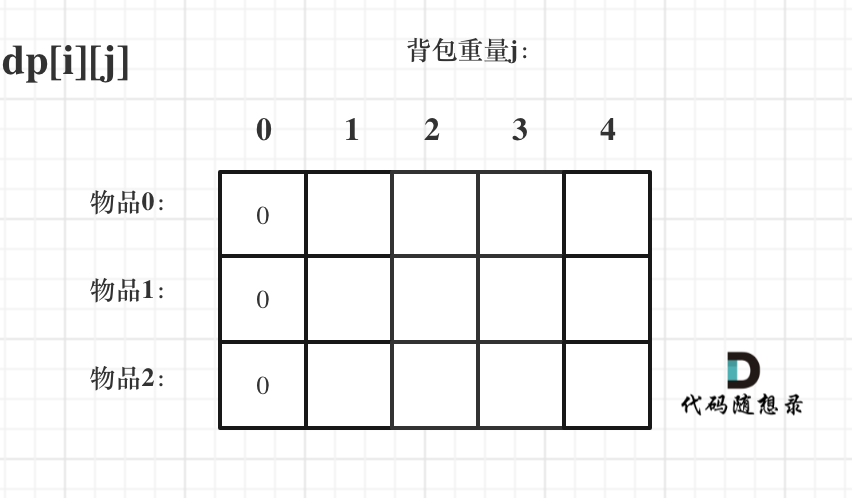
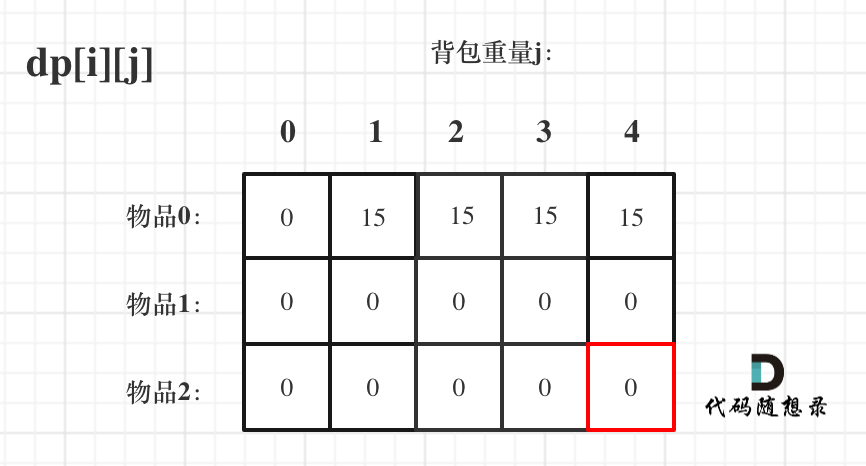
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
代码初始化如下:
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。
dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
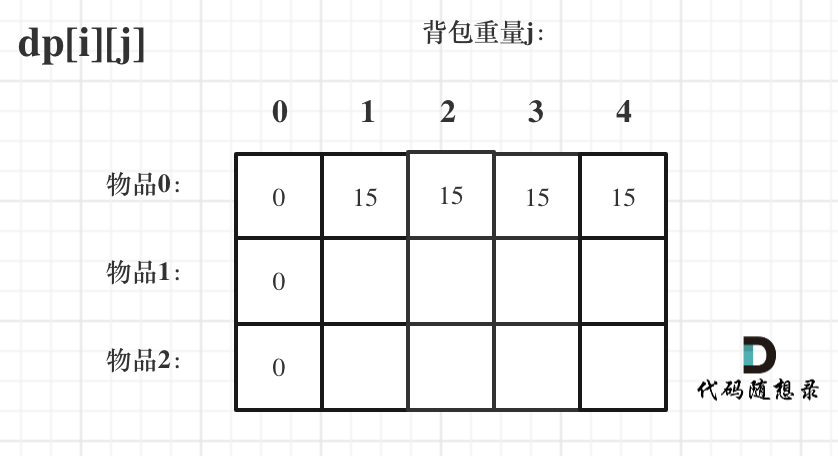
此时dp数组初始化情况如图所示:
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
初始-1,初始-2,初始100,都可以!
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
如图:
最后初始化代码如下:
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
费了这么大的功夫,才把如何初始化讲清楚,相信不少同学平时初始化dp数组是凭感觉来的,但有时候感觉是不靠谱的。
- 确定遍历顺序
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
那么问题来了,先遍历 物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
那么我先给出先遍历物品,然后遍历背包重量的代码。
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
先遍历背包,再遍历物品,也是可以的!(注意我这里使用的二维dp数组)
例如这样:
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
为什么也是可以的呢?
要理解递归的本质和递推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
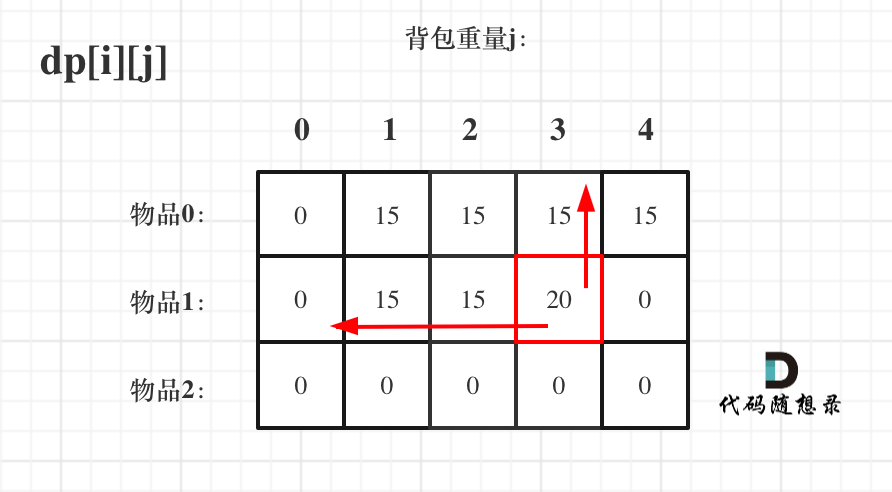
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
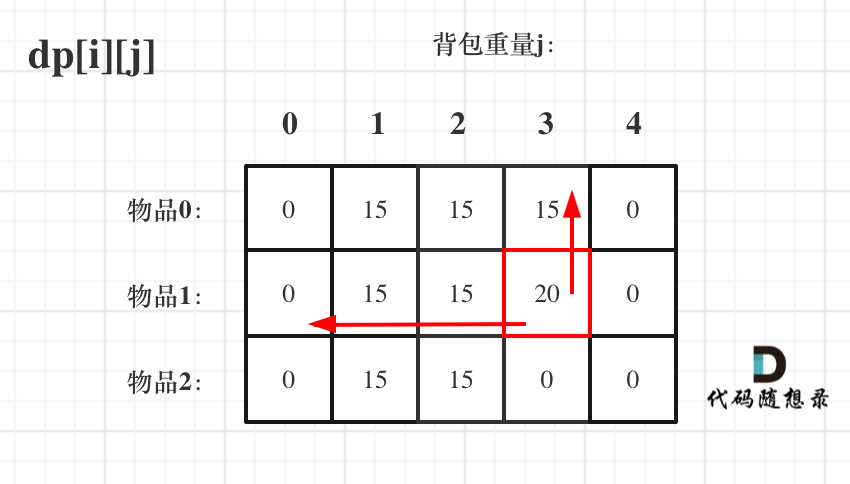
再来看看先遍历背包,再遍历物品呢,如图:
大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!
但先遍历物品再遍历背包这个顺序更好理解。
其实背包问题里,两个for循环的先后循序是非常有讲究的,理解遍历顺序其实比理解推导公式难多了。
- 举例推导dp数组
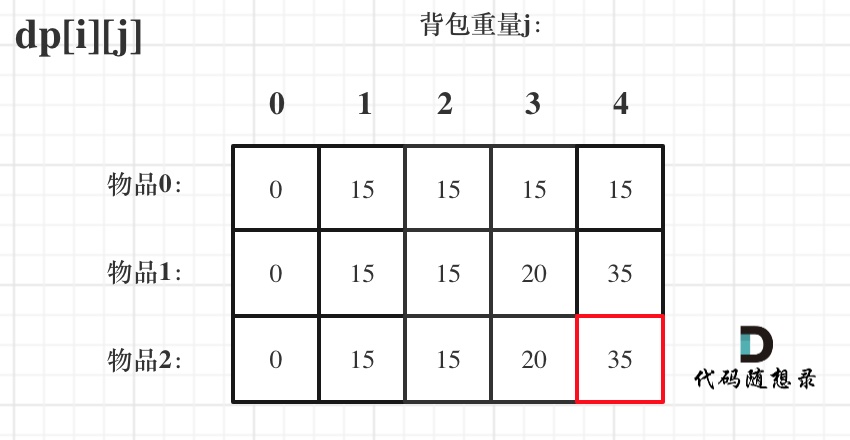
来看一下对应的dp数组的数值,如图:
最终结果就是dp[2][4]。
建议大家此时自己在纸上推导一遍,看看dp数组里每一个数值是不是这样的。
做动态规划的题目,最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下,然后在动手写代码!
很多同学做dp题目,遇到各种问题,然后凭感觉东改改西改改,怎么改都不对,或者稀里糊涂就改过了。
主要就是自己没有动手推导一下dp数组的演变过程,如果推导明白了,代码写出来就算有问题,只要把dp数组打印出来,对比一下和自己推导的有什么差异,很快就可以发现问题了。
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
讲了这么多才刚刚把二维dp的01背包讲完,这里大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上。
可能有的同学并没有注意到初始化 和 遍历顺序的重要性,我们后面做力扣上背包面试题目的时候,大家就会感受出来了。
下一篇 还是理论基础,我们再来讲一维dp数组实现的01背包(滚动数组),分析一下和二维有什么区别,在初始化和遍历顺序上又有什么差异,敬请期待!
public static void main(string[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值
int[][] dp = new int[wlen + 1][bagsize + 1];
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
//打印dp数组
for (int i = 0; i <= wlen; i++){
for (int j = 0; j <= bagsize; j++){
system.out.print(dp[i][j] + " ");
}
system.out.print("\n");
}
}def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
rows, cols = len(weight), bag_size + 1
dp = [[0 for _ in range(cols)] for _ in range(rows)]
# 初始化dp数组.
for i in range(rows):
dp[i][0] = 0
first_item_weight, first_item_value = weight[0], value[0]
for j in range(1, cols):
if first_item_weight <= j:
dp[0][j] = first_item_value
# 更新dp数组: 先遍历物品, 再遍历背包.
for i in range(1, len(weight)):
cur_weight, cur_val = weight[i], value[i]
for j in range(1, cols):
if cur_weight > j: # 说明背包装不下当前物品.
dp[i][j] = dp[i - 1][j] # 所以不装当前物品.
else:
# 定义dp数组: dp[i][j] 前i个物品里,放进容量为j的背包,价值总和最大是多少。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)
print(dp)
if __name__ == "__main__":
bag_size = 4
weight = [1, 3, 4]
value = [15, 20, 30]
test_2_wei_bag_problem1(bag_size, weight, value)func test_2_wei_bag_problem1(weight, value []int, bagweight int) int {
// 定义dp数组
dp := make([][]int, len(weight))
for i, _ := range dp {
dp[i] = make([]int, bagweight+1)
}
// 初始化
for j := bagweight; j >= weight[0]; j-- {
dp[0][j] = dp[0][j-weight[0]] + value[0]
}
// 递推公式
for i := 1; i < len(weight); i++ {
//正序,也可以倒序
for j := weight[i];j<= bagweight ; j++ {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
}
}
return dp[len(weight)-1][bagweight]
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
func main() {
weight := []int{1,3,4}
value := []int{15,20,30}
test_2_wei_bag_problem1(weight,value,4)
}function testweightbagproblem (wight, value, size) {
const len = wight.length,
dp = array.from({length: len + 1}).map(
() => array(size + 1).fill(0)
);
for(let i = 1; i <= len; i++) {
for(let j = 0; j <= size; j++) {
if(wight[i - 1] <= j) {
dp[i][j] = math.max(
dp[i - 1][j],
value[i - 1] + dp[i - 1][j - wight[i - 1]]
)
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
// console.table(dp);
return dp[len][size];
}
function testWeightBagProblem2 (wight, value, size) {
const len = wight.length,
dp = Array(size + 1).fill(0);
for(let i = 1; i <= len; i++) {
for(let j = size; j >= wight[i - 1]; j--) {
dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
}
}
return dp[size];
}
function test () {
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}
test();