selection

Selection Sort

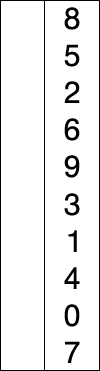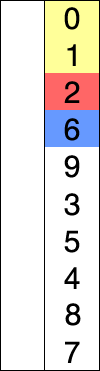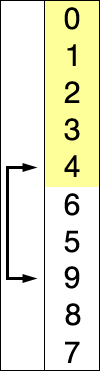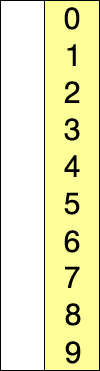
Select the minimum element and move it to its correct place in every pass

How It Works:

• Red is the current min.
• Yellow is the sorted list.
• Blue is the current item.

Time Complexity

---

1. Worst Case Complexity: O(n²) If we want to sort in ascending order and the array is in descending order then, the worst case occurs.
2. Best Case Complexity: O(n²) It occurs when the array is already sorted
3. Average Case Complexity: O(n²) It occurs when the elements of the array are in jumbled order (neither ascending nor descending).

Space Complexity

---

1. Space complexity is O(1) because an extra variable is used for swapping.

Properties

1. Comparison Based
2. Not Stable
3. Inplace
4. Basic idea for Heap Sort
5. Less memory writes compared to Bubble Sort

Applications

1. It is used when a small list is to be sorted
2. If the cost of swapping does not matter
3. If checking of all the elements is compulsory
4. If the cost of writing to a memory matters like in flash memory (number of writes/swaps is O(n) as compared to O(n²) of bubble sort)

Advantages

1. Simple and easy to understand.
2. Works well with small datasets.

Disadvantages

1. Selection sort has a time complexity of O(n²) in the worst and average case.
2. Does not work well on large datasets.
3. Does not preserve the relative order of items with equal keys which means it is not stable.