68(2)-二叉树的最近公共祖先~Easy.md

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

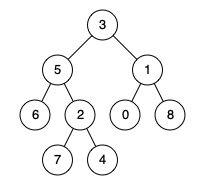
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉树中。

思路:

1. 初始化：声明res或ans用于存储最终的LCA节点。
2. 递归函数：定义一个递归函数dfs，它接收当前节点root和要寻找的两个节点p和q。
3. 基本情况：如果当前节点为空，返回false。
4. 递归搜索：对当前节点的左子树和右子树分别进行递归调用dfs。
5. 更新LCA：如果左子树和右子树都返回true，或者当前节点是p或q之一，并且至少一个子树返回true，则将当前节点设置为LCA（res = root或ans = root）。
6. 返回值：递归函数返回true，如果当前节点是p或q之一，或者任何子树返回true。
7. 最终结果：在递归结束后，返回res或ans作为LCA。

它的时间复杂度是O(n)，其中n是二叉树中节点的数量，因为每个节点恰好被访问一次。空间复杂度是O(h)，其中h是二叉树的高度，这是因为在最坏的情况下（树完全不平衡），递归堆栈可能需要存储与树的高度相等的节点数量。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
var lowestCommonAncestor = function (root, p, q) {
  let res;
  const dfs = (root, p, q) => {
    if (root === null) {
      return false;
    }
    const lson = dfs(root.left, p, q);
    const rson = dfs(root.right, p, q);
    if (
      (lson && rson) ||
      ((root.val === p.val || root.val === q.val) && (lson || rson))
    ) {
      res = root;
    }
    return lson || rson || root.val === p.val || root.val === q.val;
  };
  dfs(root, p, q);
  return res;
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

interface TreeNode {
  val: number;
}

var lowestCommonAncestor = function (root, p, q) {
  let ans;
  const dfs = (root, p, q) => {
    if (root === null) {
      return false;
    }
    const lson = dfs(root.left, p, q);
    const rson = dfs(root.right, p, q);
    if (
      (lson && rson) ||
      ((root.val === p.val || root.val === q.val) && (lson || rson))
    ) {
      ans = root;
    }
    return lson || rson || root.val === p.val || root.val === q.val;
  };
  dfs(root, p, q);
  return ans;
};