2352-EqualRowandColumnPairs.md

相等行列对

给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ，返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。

如果行和列以相同的顺序包含相同的元素（即相等的数组），则认为二者是相等的。

示例 1：

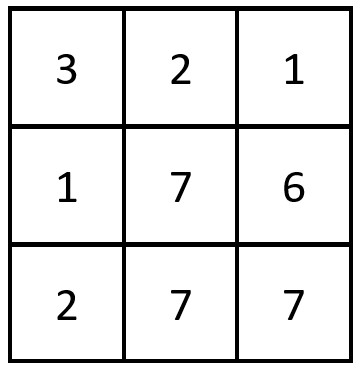
输入：grid = [[3,2,1],[1,7,6],[2,7,7]]
输出：1
解释：存在一对相等行列对：

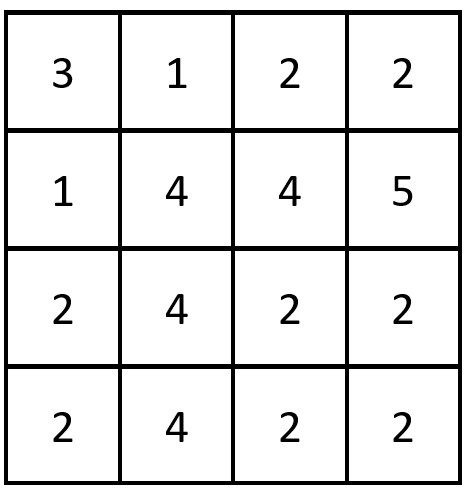
- (第 2 行，第 1 列)：[2,7,7]

示例 2：

输入：grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出：3
解释：存在三对相等行列对：

- (第 0 行，第 0 列)：[3,1,2,2]
- (第 2 行, 第 2 列)：[2,4,2,2]
- (第 3 行, 第 2 列)：[2,4,2,2]

提示：

• n == grid.length == grid[i].length
• 1 <= n <= 200
• 1 <= grid[i][j] <= 10^5

思路：

1. 存储行字符串：遍历矩阵的每一行，将行转换为字符串，并存储在 cnt 对象中，键为行字符串，值为该行字符串出现的次数。
2. 检查列：遍历矩阵的每一列，将每一列的元素也转换为字符串。
3. 计数相等对：对于每一列字符串，检查它是否在 cnt 对象中，如果在，则将该列字符串出现的次数累加到结果 res 中。
4. 返回结果：返回累加的结果 res，即为满足条件的行列对的数目。

时间复杂度：O(n^2)，其中 n 是矩阵的维度。需要遍历矩阵的每一行和每一列。 空间复杂度：O(n^2)，在最坏的情况下，每一行和每一列都是不同的，因此 cnt 对象中将存储 n^2 个不同的字符串。

var equalPairs = function (grid) {
  const n = grid.length;
  const cnt = {};

  for (const row of grid) {
    const rowStr = row.toString();
    cnt[rowStr] = (cnt[rowStr] || 0) + 1;
  }

  let res = 0;
  for (let j = 0; j < n; j++) {
    const arr = [];
    for (let i = 0; i < n; i++) {
      arr.push(grid[i][j]);
    }
    const arrStr = arr.toString();
    if (cnt[arrStr]) {
      res += cnt[arrStr];
    }
  }

  return res;
};