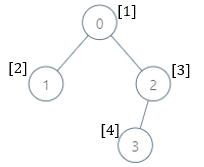
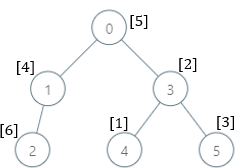
There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root, parents[0] == -1.
There are 105 genetic values, each represented by an integer in the inclusive range [1, 105]. You are given a 0-indexed integer array nums, where nums[i] is a distinct genetic value for node i.
Return an array ans of length n where ans[i] is the smallest genetic value that is missing from the subtree rooted at node i.
The subtree rooted at a node x contains node x and all of its descendant nodes.
Example 1:
Input: parents = [-1,0,0,2], nums = [1,2,3,4] Output: [5,1,1,1] Explanation: The answer for each subtree is calculated as follows: - 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value. - 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value. - 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value. - 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.
Example 2:
Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3] Output: [7,1,1,4,2,1] Explanation: The answer for each subtree is calculated as follows: - 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value. - 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value. - 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value. - 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value. - 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value. - 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.
Example 3:
Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8] Output: [1,1,1,1,1,1,1] Explanation: The value 1 is missing from all the subtrees.
Constraints:
n == parents.length == nums.length2 <= n <= 1050 <= parents[i] <= n - 1fori != 0parents[0] == -1parentsrepresents a valid tree.1 <= nums[i] <= 105- Each
nums[i]is distinct.
Companies:
Codenation
Related Topics:
Dynamic Programming, Tree, Depth-First Search, Union Find
- Only the node with value 1 and its ancestors have missing value greater than 1. All other nodes must have missing value 1.
- We traverse from the node with value 1 through its ancestors until the root. For each node, we DFS to visit all its children to collect the values we've seen.
- Based on the values we've seen, we can use a single variable
missto keep track of the first missing value. This value is monotonically increasing.
// OJ: https://leetcode.com/problems/smallest-missing-genetic-value-in-each-subtree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
// Ref: https://leetcode.com/problems/smallest-missing-genetic-value-in-each-subtree/discuss/1458486/Python-Strict-O(n)-Solution
class Solution {
public:
vector<int> smallestMissingValueSubtree(vector<int>& P, vector<int>& A) {
int N = P.size();
vector<int> ans(N, 1), seen(100002, 0);
auto it = find(begin(A), end(A), 1);
if (it == end(A)) return ans; // if there is no node with value 1, all nodes can use 1.
vector<int> children[N];
for (int i = 1; i < N; ++i) children[P[i]].push_back(i);
int i = it - begin(A), miss = 1;
function<void(int)> dfs = [&](int i) {
if (seen[A[i]]) return;
for (int j : children[i]) dfs(j);
seen[A[i]] = 1;
};
while (i > -1) { // from the node of value 1, traverse all its ancestors
dfs(i);
while (seen[miss]) miss++;
ans[i] = miss;
i = P[i];
}
return ans;
}
};