有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。
你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。
为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为 newColor 。
最后返回 经过上色渲染后的图像 。
示例 1:
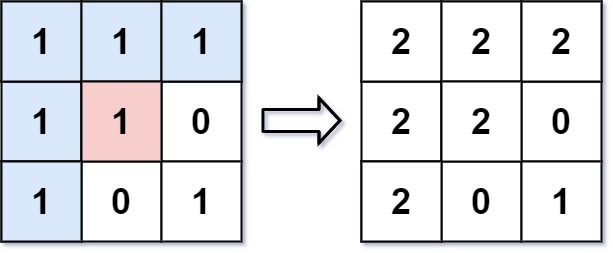
输入: image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间,(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。 注意,右下角的像素没有更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:
输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2 输出: [[2,2,2],[2,2,2]]
提示:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], newColor < 2160 <= sr < m0 <= sc < n
Flood fill 算法。
Flood fill 算法是从一个区域中提取若干个连通的点与其他相邻区域区分开(或分别染成不同颜色)的经典算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。
最简单的实现方法是采用 DFS 的递归方法,也可以采用 BFS 的迭代来实现。
DFS:
class Solution:
def floodFill(
self, image: List[List[int]], sr: int, sc: int, newColor: int
) -> List[List[int]]:
def dfs(i, j, oc, nc):
if (
i < 0
or i >= len(image)
or j < 0
or j >= len(image[0])
or image[i][j] != oc
or image[i][j] == nc
):
return
image[i][j] = nc
for x, y in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
dfs(i + x, j + y, oc, nc)
dfs(sr, sc, image[sr][sc], newColor)
return imageBFS:
class Solution:
def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
if image[sr][sc] == newColor:
return image
q = deque([(sr, sc)])
oc = image[sr][sc]
image[sr][sc] = newColor
while q:
i, j = q.popleft()
for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
x, y = i + a, j + b
if 0 <= x < len(image) and 0 <= y < len(image[0]) and image[x][y] == oc:
q.append((x, y))
image[x][y] = newColor
return imageDFS:
class Solution {
private int[][] dirs = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
dfs(image, sr, sc, image[sr][sc], newColor);
return image;
}
private void dfs(int[][] image, int i, int j, int oc, int nc) {
if (i < 0 || i >= image.length || j < 0 || j >= image[0].length || image[i][j] != oc || image[i][j] == nc) {
return;
}
image[i][j] = nc;
for (int[] dir : dirs) {
dfs(image, i + dir[0], j + dir[1], oc, nc);
}
}
}BFS:
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
if (image[sr][sc] == newColor) {
return image;
}
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[]{sr, sc});
int oc = image[sr][sc];
image[sr][sc] = newColor;
int[] dirs = {-1, 0, 1, 0, -1};
while (!q.isEmpty()) {
int[] p = q.poll();
int i = p[0], j = p[1];
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < image.length && y >= 0 && y < image[0].length && image[x][y] == oc) {
q.offer(new int[]{x, y});
image[x][y] = newColor;
}
}
}
return image;
}
}DFS:
class Solution {
public:
vector<vector<int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
dfs(image, sr, sc, image[sr][sc], newColor);
return image;
}
void dfs(vector<vector<int>>& image, int i, int j, int oc, int nc) {
if (i < 0 || i >= image.size() || j < 0 || j >= image[0].size() || image[i][j] != oc || image[i][j] == nc) return;
image[i][j] = nc;
for (auto& dir : dirs) dfs(image, i + dir[0], j + dir[1], oc, nc);
}
};BFS:
class Solution {
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
if (image[sr][sc] == newColor) return image;
int oc = image[sr][sc];
image[sr][sc] = newColor;
queue<pair<int, int>> q;
q.push({sr, sc});
vector<int> dirs = {-1, 0, 1, 0, -1};
while (!q.empty())
{
auto p = q.front();
q.pop();
for (int k = 0; k < 4; ++k)
{
int x = p.first + dirs[k];
int y = p.second + dirs[k + 1];
if (x >= 0 && x < image.size() && y >= 0 && y < image[0].size() && image[x][y] == oc)
{
q.push({x, y});
image[x][y] = newColor;
}
}
}
return image;
}
};DFS:
func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
dfs(image, sr, sc, image[sr][sc], newColor)
return image
}
func dfs(image [][]int, i, j, oc, nc int) {
if i < 0 || i >= len(image) || j < 0 || j >= len(image[0]) || image[i][j] != oc || image[i][j] == nc {
return
}
image[i][j] = nc
dirs := [4][2]int{{0, -1}, {0, 1}, {1, 0}, {-1, 0}}
for _, dir := range dirs {
dfs(image, i+dir[0], j+dir[1], oc, nc)
}
}BFS:
func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
if image[sr][sc] == newColor {
return image
}
oc := image[sr][sc]
q := [][]int{[]int{sr, sc}}
image[sr][sc] = newColor
dirs := []int{-1, 0, 1, 0, -1}
for len(q) > 0 {
p := q[0]
q = q[1:]
for k := 0; k < 4; k++ {
x, y := p[0]+dirs[k], p[1]+dirs[k+1]
if x >= 0 && x < len(image) && y >= 0 && y < len(image[0]) && image[x][y] == oc {
q = append(q, []int{x, y})
image[x][y] = newColor
}
}
}
return image
}function floodFill(
image: number[][],
sr: number,
sc: number,
newColor: number,
): number[][] {
const m = image.length;
const n = image[0].length;
const target = image[sr][sc];
const dfs = (i: number, j: number) => {
if (
i < 0 ||
i === m ||
j < 0 ||
j === n ||
image[i][j] !== target ||
image[i][j] === newColor
) {
return;
}
image[i][j] = newColor;
dfs(i + 1, j);
dfs(i - 1, j);
dfs(i, j + 1);
dfs(i, j - 1);
};
dfs(sr, sc);
return image;
}impl Solution {
fn dfs(image: &mut Vec<Vec<i32>>, sr: i32, sc: i32, new_color: i32, target: i32) {
if sr < 0 || sr == image.len() as i32 || sc < 0 || sc == image[0].len() as i32 {
return;
}
let sr = sr as usize;
let sc = sc as usize;
if sr < 0 || image[sr][sc] == new_color || image[sr][sc] != target {
return;
}
image[sr][sc] = new_color;
let sr = sr as i32;
let sc = sc as i32;
Self::dfs(image, sr + 1, sc, new_color, target);
Self::dfs(image, sr - 1, sc, new_color, target);
Self::dfs(image, sr, sc + 1, new_color, target);
Self::dfs(image, sr, sc - 1, new_color, target);
}
pub fn flood_fill(image: Vec<Vec<i32>>, sr: i32, sc: i32, new_color: i32) -> Vec<Vec<i32>> {
let target = image[sr as usize][sc as usize];
Self::dfs(&mut image, sr, sc, new_color, target);
image
}
}