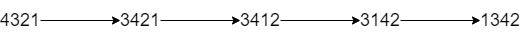README.md

1505. 最多 K 次交换相邻数位后得到的最小整数

English Version

题目描述

给你一个字符串 num 和一个整数 k 。其中，num 表示一个很大的整数，字符串中的每个字符依次对应整数上的各个 数位 。

你可以交换这个整数相邻数位的数字 最多 k 次。

请你返回你能得到的最小整数，并以字符串形式返回。

 

示例 1：

输入：num = "4321", k = 4
输出："1342"
解释：4321 通过 4 次交换相邻数位得到最小整数的步骤如上图所示。

示例 2：

输入：num = "100", k = 1
输出："010"
解释：输出可以包含前导 0 ，但输入保证不会有前导 0 。

示例 3：

输入：num = "36789", k = 1000
输出："36789"
解释：不需要做任何交换。

示例 4：

输入：num = "22", k = 22
输出："22"

示例 5：

输入：num = "9438957234785635408", k = 23
输出："0345989723478563548"

 

提示：

• 1 <= num.length <= 30000
• num 只包含 数字 且不含有 前导 0 。
• 1 <= k <= 10^9

解法

方法一：贪心算法 + 树状数组

树状数组，也称作“二叉索引树”（Binary Indexed Tree）或 Fenwick 树。 它可以高效地实现如下两个操作：

1. 单点更新 update(x, delta)： 把序列 x 位置的数加上一个值 delta；
2. 前缀和查询 query(x)：查询序列 [1,...x] 区间的区间和，即位置 x 的前缀和。

这两个操作的时间复杂度均为 O(log n)。

对于本题，要想得到在 k 次交换内字典序最小整数，我们可以「贪心」地从 num 的最高位开始考虑，即希望 num 的最高位尽可能小。我们可以依次枚举 0~9，对于当前枚举到的数位 x，判断是否可以将某个位置上的 x 通过最多 k 次交换移动到最高位。由于每一次交换只能交换相邻位置的两个数字，因此将一个距离最高位为 s 的数位移动到最高位，需要 s 次交换操作。例如当 num = 97620 时，0 与最高位的距离为 4，我们可以通过 4 次交换操作把 0 移动到最高位。

这样的交换操作相当于把 0 移动到最高位，同时将 0 之前的所有数位向后移动了一位。

我们接下来考虑次高位。与最高位类似，我们选择最小的数位 x，使得它与次高位的距离不超过 k'，其中 k' 是 k 扣除最高位交换后的剩余次数。

考虑上面 num = 97620 的例子，此时我们应当选择 x=2 交换至次高位。然而我们发现，经过第一次的交换操作，2 所在的位置发生了变化！在 num 中，2 与次高位的距离为 2，而将 0 交换至最高位后，2 与次高位的距离增加了 1，变为 3。这是因为 0 从 2 的后面「转移」到了 2 的前面，使得 2 向后移动了一位。因此，x 实际所在的位置，等于 x 初始时在 num 中的位置，加上 x 后面发生交换的数位个数。这里的「x 后面发生交换的数位个数」，就可以使用树状数组进行维护。

解题思路如下：

1. 用 pos[x] 按照高位到低位的顺序，存放所有 x 在 num 中出现的位置；
2. 从高到低遍历每一个位置。对于位置 i，我们从小到大枚举交换的数位 x。pos[x] 中的首个元素即为与当前位置距离最近的 x 的位置：
   • 记 j 为 pos[x] 中的首元素，那么 num[j]（也即是 x）当前实际所在的位置，等于 j 加上 j 后面发现交换的数位个数。我们使用树状数组查询区间 [j + 1, n]，那么 num[j] 与位置 i 的实际距离 dist 为：tree.query(n) - tree.query(j) + j - i。
   • 如果 dist 小于等于 k，那么我们可以将 x 交换至位置 i。我们使用树状数组更新单点 j，将对应的值增加 1，表示该位置的数位发生了变换。随后更新 k 值，以及将 j 从 pos[x] 中移除。
3. 遍历结束后，我们就得到了答案。

Python3

class BinaryIndexedTree:
    def __init__(self, n):
        self.n = n
        self.c = [0] * (n + 1)

    @staticmethod
    def lowbit(x):
        return x & -x

    def update(self, x, delta):
        while x <= self.n:
            self.c[x] += delta
            x += BinaryIndexedTree.lowbit(x)

    def query(self, x):
        s = 0
        while x:
            s += self.c[x]
            x -= BinaryIndexedTree.lowbit(x)
        return s


class Solution:
    def minInteger(self, num: str, k: int) -> str:
        pos = defaultdict(deque)
        for i, v in enumerate(num, 1):
            pos[int(v)].append(i)
        ans = []
        n = len(num)
        tree = BinaryIndexedTree(n)
        for i in range(1, n + 1):
            for v in range(10):
                q = pos[v]
                if q:
                    j = q[0]
                    dist = tree.query(n) - tree.query(j) + j - i
                    if dist <= k:
                        k -= dist
                        q.popleft()
                        ans.append(str(v))
                        tree.update(j, 1)
                        break
        return ''.join(ans)

Java

class Solution {
    public String minInteger(String num, int k) {
        Queue<Integer>[] pos = new Queue[10];
        for (int i = 0; i < 10; ++i) {
            pos[i] = new ArrayDeque<>();
        }
        int n = num.length();
        for (int i = 0; i < n; ++i) {
            pos[num.charAt(i) - '0'].offer(i + 1);
        }
        StringBuilder ans = new StringBuilder();
        BinaryIndexedTree tree = new BinaryIndexedTree(n);
        for (int i = 1; i <= n; ++i) {
            for (int v = 0; v < 10; ++v) {
                if (!pos[v].isEmpty()) {
                    Queue<Integer> q = pos[v];
                    int j = q.peek();
                    int dist = tree.query(n) - tree.query(j) + j - i;
                    if (dist <= k) {
                        k -= dist;
                        q.poll();
                        ans.append(v);
                        tree.update(j, 1);
                        break;
                    }
                }
            }
        }
        return ans.toString();
    }
}

class BinaryIndexedTree {
    private int n;
    private int[] c;

    public BinaryIndexedTree(int n) {
        this.n = n;
        c = new int[n + 1];
    }

    public void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    public int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    public static int lowbit(int x) {
        return x & -x;
    }
}

C++

class BinaryIndexedTree {
public:
    int n;
    vector<int> c;

    BinaryIndexedTree(int _n)
        : n(_n)
        , c(_n + 1) { }

    void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    int lowbit(int x) {
        return x & -x;
    }
};

class Solution {
public:
    string minInteger(string num, int k) {
        vector<queue<int>> pos(10);
        int n = num.size();
        for (int i = 0; i < n; ++i) pos[num[i] - '0'].push(i + 1);
        BinaryIndexedTree* tree = new BinaryIndexedTree(n);
        string ans = "";
        for (int i = 1; i <= n; ++i) {
            for (int v = 0; v < 10; ++v) {
                auto& q = pos[v];
                if (!q.empty()) {
                    int j = q.front();
                    int dist = tree->query(n) - tree->query(j) + j - i;
                    if (dist <= k) {
                        k -= dist;
                        q.pop();
                        ans += (v + '0');
                        tree->update(j, 1);
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

Go

type BinaryIndexedTree struct {
	n int
	c []int
}

func newBinaryIndexedTree(n int) *BinaryIndexedTree {
	c := make([]int, n+1)
	return &BinaryIndexedTree{n, c}
}

func (this *BinaryIndexedTree) lowbit(x int) int {
	return x & -x
}

func (this *BinaryIndexedTree) update(x, delta int) {
	for x <= this.n {
		this.c[x] += delta
		x += this.lowbit(x)
	}
}

func (this *BinaryIndexedTree) query(x int) int {
	s := 0
	for x > 0 {
		s += this.c[x]
		x -= this.lowbit(x)
	}
	return s
}

func minInteger(num string, k int) string {
	pos := make([][]int, 10)
	for i, c := range num {
		pos[c-'0'] = append(pos[c-'0'], i+1)
	}
	n := len(num)
	tree := newBinaryIndexedTree(n)
	var ans strings.Builder
	for i := 1; i <= n; i++ {
		for v := 0; v < 10; v++ {
			if len(pos[v]) > 0 {
				j := pos[v][0]
				dist := tree.query(n) - tree.query(j) + j - i
				if dist <= k {
					k -= dist
					pos[v] = pos[v][1:]
					ans.WriteByte(byte(v + '0'))
					tree.update(j, 1)
					break
				}
			}
		}
	}
	return ans.String()
}

...