지금까지 모노이드에 대한 많은 공식을 봤었습니다. 집합으로써, 대상이 하나인 카테고리로써, 모노이달 카테고리의 대상으로써. 이것들을 하나의 단순한 컨셉으로 축약시킬 수 있을까요?
집합 m과 다음 함수 쌍을 지니는 모노이드로부터 시작해봅시다.
𝜇∷𝑚×𝑚→𝑚
𝜂∷1→𝑚
여기서 1은 Set의 터미널 오브젝트 입니다. - 싱글톤 셋. 첫번째 함수는 multiplication을 정의합니다.(원소 쌍을 받아 그들의 곱을 반환 합니다.) 두번째는 m에서 unit 원소를 선택해 냅니다. 이 두 함수만 가지고는 모노이드를 정의할 수 없습니다. 그러기 위하여 결합법칙, 유닛 법칙과 같은 추가적인 조건이 필요합니다. 하지만 지금은 이를 생각하지말고 "잠재적으로 모노이드"가 될 수 있는 구조에 대하여만 생각해보죠. 함수의 쌍은 두 함수 집합의 카르테시안 곱의 원소입니다. 그리고 이 집합은 익스포넨셜 오브젝트로 나타낼 수 있음을 압니다.
𝜇 ∈ 𝑚^𝑚×𝑚
𝜂 ∈ 𝑚1
이 두 집합의 카르테시안 곱은 다음과 같습니다.
m^mxm x m^1
고등학교때 배운 대수학을 이용하여(Cartesian closed category에 적용되는) 다음과 같이 쓸 수 있습니다.
m x m + 1 -> m
이제 이 함수들의 집합의 모든 원소는 잠재적으로 모노이드라고 할 수 있습니다.
이 공식의 장점은 이를 통해 흥미로운 일반화에 도달할 수 있다는 점 입니다. 예를들어 이 언어를 이용해 그룹을 어떻게 묘사할까요? 그룹은 추가적인 함수 - 모든 원소를 뒤집는 - 를 지니는 모노이드 입니다. 이 함수는 m -> m이라 씁니다. 예를들어 + 연산자가 이항 연산 0이 유닛, 그리고 음수가 인버스인 정수는 그룹을 이룹니다. 그룹을 정의하기위해 다음 3개의 함수로 시작합니다.
m x m -> m
m -> m
1 -> m
위에서 보았듯이 이 함수들을 하나의 함수 집합으로 결합할 수 있습니다.
m x m + m + 1 -> m
이항 연산자 (덧셈) 부터 시작하여 단항 연산자(네거티브), 그리고 nullary 연산자(identity - 여기서는 0) 로 시작하였습니다. 이들을 하나의 함수로 결합할 수 있습니다. 이 시그니처를 지니는 함수들의 집합은 잠재적인 그룹입니다.
이와같은짓을 계속할 수 있습니다. 예를들어 링을 정의해보죠. 추가적인 이항 연산자와 nullary 연산자를 더하며 계속합니다. 그럴때마다 결과는 좌변에는 제곱된 결과들의 합(0-power도 포함 - 여기서는 터미널 오브젝트) 그리고 우변은 자기 자신이 됩니다.
이제 이 일반화를 미친듯이 해보죠. 첫째로 대상과 함수의 집합을 사상으로 바꿉니다. n차의 연산자를 n차의 프로덕트에서 시작하는 사상으로 바꿀 수 있습니다. nullary 연산자를 위해서는 터미널 오브젝트가 존재해야합니다. 그렇기에 카르테시안 카테고리가 필요합니다. 이 연산자들을 합치기 위하여 익스포넨셜이 필요하고 그렇기에 이는 Cartesian closed category 입니다. 마지막으로 이 대수학 헛소리?(shenanigans) 들을 완성하기 위하여 coproduct가 필요합니다.
대안적으로 이 공식들과 이들을 최종적인 프로덕트로 압축시키는 것을 잊을 수 있는 방법이 있습니다. 사상의 좌변에 있는 프로덕트들의 합은 엔도펑터를 정의합니다. 그러면 대신 임의의 엔도펑터 F를 고르는거는 어떨까요? 이경우에 카테고리에 어떤 제약조건도 부여할 필요가 없습니다. 이경우에 이루가 얻게되는것을 F-algebra라 부릅니다.
F-algebra는 엔더펑터 F, 대상 a 그리고 사상 F a -> a로 구성됩니다. 여기서 대상은 종종 carrier라 불립니다.(내재된 대상 혹은 프로그래밍적 문맥에서 케리어 타입) 사상은 종종 evaluation function이나 structure map이라 불립니다. 펑터 F를 수식을 형성하는 것으로 생각하고 사상을 evaluating 하는 것으로 생각하세요.
하스켈에서 F-algebra의 정의는 다음과 같고 이는 그것의 evaluation function과 함께 algebra를 정의합니다.
type Algebra f a = f a -> a모노이드 예제에서 질문에 해당하는 펑터는 다음과 같습니다.
data MonF a = MEmpty | MAppend a a
-- 1 + a x a 을 위한 하스켈 코드그리고 링은 다음과같은 펑터로 정의될 것 입니다.
data RingF a = RZero
| ROne
| RAdd a a
| RMul a a
| RNeg a
-- 1 + 1 + a x a + a x a + a정수집합에 대한 링 예를 들어보죠. 여기서 Integer를 케리어 타입으로 선택하였고 evaulation function을 다음과 같이 정의합니다.
evalZ :: Algebra RingF Integer
evalZ RZero = 0
evalZ ROne = 1
evalZ (RAdd m n) = m + n
evalZ (RMul m n) = m * n
evalZ (RNeg n) = -n동일한 RingF를 기반으로 하는 더 많은 F-algebra 가 있습니다. 메트릭스 케이스도 예를 들 수 있습니다.
보이는것과 같이 펑터의 역할은 algebra의 evaluator로 evaluated 될 수 있는 수식을 만드는 것 입니다. 지금까지 간단한 수식만을 보았습니다. 재귀를 이용하면 더 정교한 표현을 만들어 낼 수 있습니다.
임의의 수식 트리를 만들 수 있는 방법은 펑터의 정의 내부에 있는 a 변수를 재귀로 치환하는 것 입니다. 예를들어 링에 대한 임의의 수식은 다음과 같은 트리구조를 만들어 냅니다.
data Expr = RZero
| ROne
| RAdd Expr Expr
| RMul Expr Expr
| RNeg Expr원래 링의 evaluator를 재귀로 다음과같이 바꿀 수 있습니다.
evalZ :: Expr -> Integer
evalZ RZero = 0
evalZ ROne = 1
evalZ (RAdd e1 e2) = evalZ e1 + evalZ e2
evalZ (RMul e1 e2) = evalZ e1 * evalZ e1
evalZ (RNeg e) = -(evalZ e)이는 모든 정수를 각각의 합으로 표현하여야하기 때문에 아직 실용적이지는 않습니다.
하지만 수식 트리를 F-algebra를 이용하여 어떻게 나타낼까요? 펑터의 정의에서 free type 변수를 교체하여 재귀적으로 바꾸는 과정을 어떻게든 공식화 해야 합니다. 이를 1-뎁스 부터 시작해보죠
type RingF1 a = RingF (RingF a)RingF1이 RingF a 에서 만들어진 RingF라 하면 비슷하게 RingF2도 정의할 수 있습니다.
type RingF2 a = RingF (RingF (RingF a))
-- 아래와같이 쓸수도 있음
type RingF2 a = RingF (RingF1 a)이 과정을 계속한다면 이 방정식의 심볼을 다음과 같이 쓸수있습니다.
type RingFn+1 a = RingF (RingFn a)개념적으로 이를 무한하게 반복하면 Expr에 도달할것입니다. Expr은 a에 의존이 없다는 점에 주목하세요. 시작점은 중요하지 않습니다. 언제나 같은 결과를 얻게됩니다. 이는 모든 임의의 엔도펑터나 카체고리에서 언제나 참은 아닙니다. 하지만 Set에서는 작동합니다.
물론 이는 논란의 여지가 있으며 나중에 더 엄격하게 만들겠습니다.
엔도펑터는 무한히 적용한 결과 fixed point라는 대상은 만들어 냅니다.
Fix f = f (Fix f)
위의 정의에서 얻을 수 있는 교훈은 Fix f를 얻기 위해 f를 무한히 적용한 결과는 한번더 적용한것과 다른점이 없다는 것 입니다. 하스켈에서 fixed point는 다음과 같이 정의됩니다.
newtype Fix f = Fix (f (Fix f))타입 생성자의 이름이 타입 이름과 다음과 같이 다르다면 더 읽기 편할것 입니다.
newtype Fix f = In (f (Fix f))하지만 Fix 생성자를 이용하죠. 이는 다음과 같은 함수 입니다.
Fix :: f (Fix f) -> Fix f또한 한수준의 펑터 적용을 벗겨내는 함수도 있습니다.
unFix :: Fix f -> f (Fix f)
unFix (Fix x) = x두 함수는 서로 역입니다. 이 함수들을 나중에 사용할 것 입니다.
이제 이책에서 자주 등장하는 트릭입니다. 어떤 새로운 대상의 구조를 생각할때마다 이것이 카테고리를 이루는지 생각해보세요. 놀랍지도않게 주어진 엔도 펑터 F에 대한 algebra는 카테고리를 형성 합니다. 이 카테고리의 대상은 algebra 입니다 - 케리어 오브젝트 a와 사상 F a -> a으로 이루어진, 이 둘은 원래의 카테고리 C에 속합니다.
이를 완성하기 위하여 F-algebra의 카테고리의 사상을 정의해야 합니다. 이 사상은 한 algebra (a, f)를 다른 algebra (b, f)로 매핑 해야 합니다. 우리는 이를 캐리어를 매핑하는 사상 m으로, 원래의 카테고리에서 a -> b 에 해당하는 사상에서 온것으로 정의할것입니다. 다른 사상은 해당하지 않습니다: 두개의 evaluator와 호환되는 사상이 필요합니다. (이와같이 구조를 보존하는 사상을 homomorphism이라 부릅니다.) 아래는 F-algebra의 homomorphism를 정의하는 방법입니다. 우선 m을 다음과 같이 리프팅 했다는것을 주목하세요.
F m :: F a -> F b
그러고난 이후에 b를 얻기 위하여 g를 타고 가봅시다. 비슷하게 f로 먼저 a 로 간뒤 m을 통하여 b에 도달할 수 있습니다. 이경우 두개의 경로가 동일하기를 원합니다.
g . F m = m . f
이것이 참으로 카테고리인지 확신하는것은 쉽습니다(힌트: C의 identity 사상은 만족할것이고 두 homomorphism의 합성은 homomorphism 입니다.)
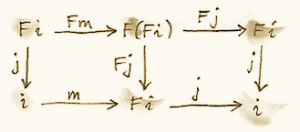
이니셜 오브젝트가 F-algebra의 카테고리에 존재한다면 이는 initial algebra라 부릅니다.이 algebra의 캐리어를 i, evaluator를 j :: F i -> i 라 부릅시다. 이경우 initial algebra의 evaluator는 동형사상임이 나타납니다. 이 결과는 Lambek의 이론으로 알려져 있습니다. 증명은 다음을 기반으로 합니다: m은 homomorphism 이기 때문에 다음의 다이어그램을 가환하게하는 이니셜 오브젝트로부터 다른 모든 F-algebra로 향하는 유일한 homomorphism m이 존재하여야합니다.
이제 캐리어가 F i 인 algebra를 만들어 봅시다. 이 algebra의 evaluator는 다음과 같아야 합니다: F (F i) -> F i 우리는 이를 j를 리프팅하여 간단하게 만들 수 있습니다.
F j :: F (F i) -> F i
(i, j)는 initial algebra 이기때문에 (F i, F j)로 향하는 유일한 homomorphism m이 존재하여야 하고 아래의 다이어그램은 가환하여야 합니다.
그리고 다음과 같은 가환 다이어그램도 얻을 수 있습니다.
여기서 j는 (F i, F j)를 (i, j)로 매핑하는 모든 algebra의 homomorphism으로 해석할 수 있습니다. 두 다이어그램을 합치면 다음과 같습니다.
이제 이 다이어그램은 j . m이 algebra의 homomorphism으로 해석될 수 있음을 보입니다. 이경우에만 두 algebra가 같습니다. 더욱이 (i, j)는 initial algebra 이기 때문에 스스로에서 스스로로 향하는 homomorphism이 하나 존재하는데 이는 idi 입니다 - 이것이 algebra의 homomorphism이라는 것을 알고있습니다. 그러므로 j . m = idi 입니다. 이 사실과 다이어그램의 좌측 가환 특성을 이용하여 m . j = id Fi임을 증명할 수 있습니다.(맨 왼쪽 수직 방향의 j이후 m) 이는 m이 j의 인버스라는것을 보이고 그러므로 j는 F i, i 사이에 동형사상입니다.
𝐹𝑖≅𝑖
그러나 이것은 i가 F의 fixed point라는 점을 의미합니다. 이것은 완벽하지 않은 주장의 공식적인 증거입니다?(That’s the formal proof behind the original hand-waving argument.)
하스켈로 돌아와 i는 Fix f에 해당하고 j는 생성자 Fix에 해당합니다. 그리고 이의 역은 unFix입니다. Lambek의 이론은 만일 initial lagebra를 얻을 수 있다면 펑터 f를 취하고 어규먼크 a를 Fix f로 바꿀 수 있음을 말합니다. fixed point가 왜 a에 의존이 없는지 보았었습니다.
자연수는 역시 F-algebra로 정의될 수 있습니다. 시작점은 다음과같은 사상 쌍 입니다.
zero :: 1 -> N
succ :: N -> N
첫번째 사상을 zero를 선택해내고 두번째의 경우 모든 자연수를 다음수로 매핑합니다. 전에 이 둘을 하나로 합칠수있었습니다.
1 + N -> N
하스켈에서 좌변은 펑터를 정의하고 다음과 같이 쓸 수 있습니다.
data NatF a = ZeroF | SuccF a이 펑터에 대한 fixed point는(initial algebra가 만들어내는) 하스켈에서 다음과같이 인코딩될수 있습니다.
data Nat = Zero | Succ Nat자연수는 0이거나 다른 자연수의 다음 수 입니다. 이는 자연수에대한 Peano representation로 알려져 있습니다.
initiality condition을 하스켈로 써봅시다. initial algebra는 Fix f로, evaluator는 constructor Fix로 다시 쓸 수 있습니다. 그리고 initial algebra에서 동일한 펑터를 이용하여 다른 algebra로 가는 유일한 사상 m이 있습니다. 캐리어가 a이고 evaluator가 alg인 algebra를 하나 선택해봅시다.
m이 무엇인지에 집중하세요: 이는 fixed point의 evaluator이고 전체 재귀 수식 트리에 대한 evaluator 입니다. 이를 구현할 수 있는 일반적인 방법을 찾아봅시다.
Lambek의 이론에 의해 Fix 생성자는 동형사상임을 나타내고 우리는 이를 unFix라 부르기로 하였습니다. 그러므로 위의 다이어그램에서 하나의 화살표를 아래와 같이 뒤집을 수 있습니다.
이 다이어그램의 가환조건을 작성해 봅시다.
m = alg . fmap m . unFix이 방정식을 m에 대한 재귀적인 정의라 해석할 수 있습니다.이 재귀는 펑터 f으로 인해 만들어지는 유한한 트리에 의해 종료되도록 묶여있습니다. fmap m이 펑터 f의 최상층 아래에서 동작하는 것을 알 수 있습니다. 다시말해서 이는 본래 트리의 자식에서 동작합니다. 그리고 자식은 항상 본래의 트리보다 한수준 아래에 있습니다.
이는 Fix f를 사용하여 구성된 트리에 m을 적용할 때 발생하는 일 입니다. unFix의 동작은 생성자를 벗겨내고, 트리의 상위레벨을 노출 시킵니다. 그런 다음 m을 최상위 노드의 모든 자식에 적용하면 타입 a라는 결과를 만들어 냅니다. 마지막으로 이 결과들을 재귀적이지 않은 evaluator alg을 이용하여 결합시킵니다. 여기서 중요한점은 evaluator alg이 재귀적이지 않은 단순한 함수라는 점 입니다.
이를 모든 algebra에 대해서 할 수 있기때문에 algebra를 파라미터로 받아 m라 불렀던 함수를 반환하는 고차함수를 만들 수 있습니다. 그리고 이 고차함수는 catamorphism이라 불립니다.
cata :: Functor f => (f a -> a) -> Fix f -> a
cata alg = alg . fmap (cata alg) . unFix자연수를 나타내는 펑터로 예를 들어 봅시다.
dtat NatF = ZeroF | SuccF a(Int, Int)를 캐리어 타입으로 선택하고 algebra를 다음과 같이 정의합시다:
fib :: NatF (Int, Int) -> (Int, Int)
fib ZeroF = (1, 1)
fib (SuccF (m, n)) = (n, m + n)이 algebra를 위한 catamorphism cata fib가 ㅠㅏ보나치 넘버를 계산해낸다는 것을 확인할 수 있을것 입니다.
일반적으로 NatF를 위한 algebra는 재귀적인 관계를 만들어 냅니다: 이전 요소의 관점에서의 현재 요소 값. 그런다음 catamorphism은 해당 시퀀스의 n번째 요소를 평가합니다.
아래의 펑터에서 e의 리스트는 initial algebra 입니다.
data ListF e a = NilF | ConsF e a실제로 변수 a를 List e라 불리는 재귀적인 결과로 바꾼다면 다음과 같은 결과를 얻을 수 있습니다.
data List e = Nil | Cons e (List e)List 펑터를 위한 algebra는 특별한 캐리어 타입을 선택하고 두 생성자에 패턴매칭을 하는 함수를 정의합니다. NilF를 위한 값은 empty list를 어떻게 evaluate 해야할지 보여주고, ConsF를 위한 값은 현재의 값이 어떻게 이전에 축적된 값과 결합되는지를 보여줍니다.
예를들어 다음은 리스트의 길이를 구하는 algebra 입니다.(캐리어 타입은 Int)
lenAlg :: ListF e Int -> Int
lenAlg (ConsF e n) = n + 1
lenAlg NilF = 0실제로 catamorphism cat lenAlg은 리스트의 길이를 계산합니다. evaluator는 리스트와 accumulator를 받아 새로운 accumulator를 반환하는 함수임에 주목하세요. 그리고 여기서는 zero라는 시작값에서 부터 시작합니다. 값의 타입과 accumulator의 타입은 캐리어 타입에 의해 주어집니다.
이를 전통적인 하스켈에서의 정의와 비교해 보세요.
length = foldr (\e n -> n + 1) 0foldr의 두 어규먼트는 algebra의 두 컴포넌트와 정확하게 일치합니다.
다른 예를 들어봅시다.
sumAlg :: List Double Double -> Double
sumAlg (ConsF e s) = e + s
sumAlg NilF = 0.0
-- again, compare this with:
sum = foldr (\e s -> e + s) 0.0위에서 보듯이 foldr은 리스트의 편리한 catamorphism 입니다.
일반적으로 화살표가 반대 방향인 dual인 F-coalgebra가 존재합니다.
a -> F a
주어진 펑터에 대한 Coalgebra 역시 카테고리를 형성하고 homomorphism은 coalgebra의 구조를 보존합니다. 이 카테고리에서 터미널 오브젝트 (t, u)는 터미널 혹은 파이널 coalgebra로 불립니다. 모든 (a, f)에 대하여 아래의 다이어그램을 가환하게 만드는 유일한 homomorphism m이 존재합니다.
사상 u :: t -> F t가 동형사상이라는 점에서 터미널 오브젝트는 펑터의 fixed point 입니다. (coalgebra를 위한 Lambek 이론)
𝐹𝑡≅𝑡
터미널 coalgebra는 일반적으로 프로그래밍에서 (가능성이 무한한) 데이터 구조 또는 전환 시스템을 생성하기 위한 레시피로 해석됩니다.
catamorphism이 initial algebra를 evaluate 하기위해 쓰이듯이 anamorphism은 terminal coalgebra를 coevaluate 하기 위해 쓰입니다.
ana :: Functor f => (a -> f a) -> a -> Fix f
ana coalg = Fix . fmap(ana coalg) . coalgcoalgebra의 표준적인 예는 fixed point가 엘러먼트 타입 e인 무한한 스트림인 펑터를 기반으로 합니다.
data StreamF e a = StreamF e a
deriving Functor
-- and this is its fixed point:
data Stream e = Stream e (Stream e)StreamF e를 위한 coalgebra는 타입 a 시드를 받아 엘리먼트와 다음 시드로 구성되는 페어를 생산하는 함수입니다.
제곱 또는 역수 리스트를 만들어내는 무한한 시퀀스를 만들어내는 coalgebra의 다른 예를 쉽게 들 수 있습니다.
coalgebra의 재미있는 예는 소수 목록을 생성하는 경우 입니다. 여기서 트릭은 캐리어 타입이 무한한 리스트입니다. 스타팅 시드는 [2...] 이고 다음 시드는 이 리스트의 tail에서 2의 배수를 모두 제거한 리스트 입니다. 그러기에 이는 3부터 시작하는 홀수 리스트 입니다. 다음 스탭에서 이를 반복합니다. 에라토스테네스의 체가 어떻게 만들어지는지 알아차릴 수 있을것 입니다.
era :: [Int] -> StreamF Int [Int]
era (p : ns) = StreamF p (filter (notdiv p) ns)
where notdiv p n = n `mod` p /= 0이 coalgebra의 anamorphism은 소수 목록을 만들어 냅니다.
primes = ana era [2..]stream은 무한한 리스트이기 때문에 하스켈의 리스트로 바꿀 수 있어야 합니다. 그러기 위해서 algebra를 형성하는 동일한 StreamF 펑터를 이용할 수 있습니다. 그리고 이를 통해 catamorphism을 수행할 수 있습니다. 예를들어 아래는 stream을 list로 바꾸는 catamorphism 입니다.
toListC :: Fix (StreamF e) -> [e]
toListC = cata al
where al :: StreamF e [e] -> [e]
al (StreamF e a) = e : a여기서 동일 엔도펑터에 대하여 fixed point는 동시에 initial algebra이며 terminal coalgebra 입니다.(Here, the same fixed point is simultaneously an initial algebra and a terminal coalgebra for the same endofunctor.) 임의의 카테고리에서 언제나 위와 같지는 않습니다. 일반적으로 엔도펑터는 많은(혹은 하나도 없는) fixed point를 지니고 있습니다. 이 initial algebra는 least fixed point라 불리고 terminal coalgebra는 greatest fixed point라 불립니다. 그러나 하스켈에서는 둘다 동일한 공식으로 정의되며 일치합니다.
리스트에 대한 anamorphism은 unfold라 불립니다. 유한한 리스트를 만들기 위해, 펑터는 Maybe 쌍을 만들도록 수정됩니다.
unfoldr :: (b -> Maybe (a, b)) -> b -> [a]Nothing은 리스트를 만드는것을 종료시킬것 입니다.
lense와 연관지을때 coalgebra는 흥미롭습니다. lense는 getter, setter 쌍으로 표현될 수 있습니다.
set :: a -> s -> a
get :: a -> s여기서 a는 대게 타입 s 필드와 함께 product 입니다.getter는 필드에 해당하는 값을 불러오고 setter는 필드에 해당하는 값을 교체합니다. 이 두 함수는 다음과 같이 하나로 합쳐질 수 있습니다.
a -> (s, s -> a)
-- We can rewrite this function further as:
a -> Store s a
-- where we have defined a functor
data Store s a = Store (s -> a) s이것이 product의 sum으로 이루어진 간단하지 않은 algebraic functor임을 주목하세요. 이는 익스포넨셜 a^s를 포함합니다.
lens는 위에서 캐리어 타입 a와 함께 이 펑터의 coalgebra 입니다. 또한 Store s 가 코모나드임을 이전에 보았었습니다. 이는 잘 작동하는?(behaved) lens는 코모나드 구조와 호환되는 coalgebra에 해당한다는 것을 알 수 있습니다. 다음 섹션에서 이를 알아볼것입니다.