Skip to content

Latest commit

 

History

History
691 lines (591 loc) · 15.6 KB

2018-04-24-algorithm-stack.md

File metadata and controls

691 lines (591 loc) · 15.6 KB
Raw

Stack

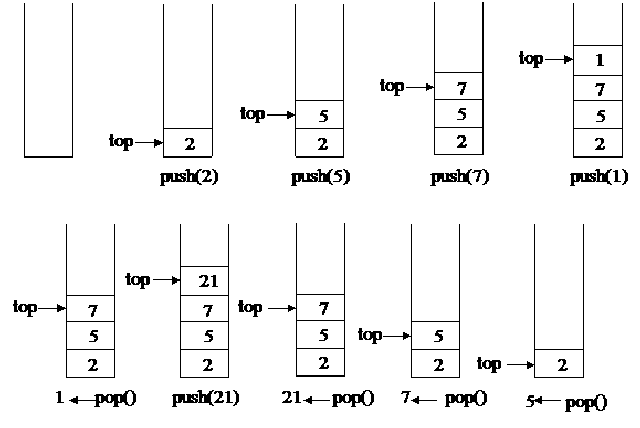
스택은 한쪽 끝에서만 자료를 넣고 뺄 수 있는 자료구조이다.

  • LIFO(Last In First Out) 마지막으로 넣은 것이 가장 먼저 나온다. 즉, 입력순서와 역순의 출력이 필요한 경우에 사용하는 것이 좋다.
    • 에디터에서 되돌리기(undo) 기능
    • 함수 호출 시 복귀주소 기억

연산 설명
push 스택에 자료를 넣는 연산
pop 스택에서 자료를 빼는 연산
top / peak 스택의 가장 위에 있는 자료를 보는 연산
empty 스택이 비어있는지 아닌지를 알아보는 연산
full 스택이 포화상태인지 검사하는 연산
size 스택에 저장되어있는 자료의 개수를 알아보는 연산

스택의 구현

배열

  • 장점 : 1차원 배열로 쉽게 구현할 수 있다.
  • 단점 : 물리적으로 크기가 고정된 배열을 사용하므로 스택의 크기 변경이 어렵다.
#include <stdio.h>
#define MAX 20

typedef struct{
    int stack[MAX];
    int top;    //stack이 비어있을 경우 -1
}StackType;

void init(StackType *s);
int is_full(StackType *s);
int is_empty(StackType *s);
int peak(StackType *s);
void push(StackType *s, int );
int pop(StackType *s);
//스택 초기화
void init(StackType *s){
    s->top = -1;
}

int is_empty(StackType *s){
    return (s->top == -1);
}

int is_full(StackType *s){
    return (s->top == MAX-1);
}

int peak(StackType *s){
    if(is_empty(s)){
        printf("스택이 비어있습니다.");
        return -1;
    }else return s->stack[s->top];
}

void push(StackType *s, int data){
    if(is_full(s)){
        printf("스택에 공간이 없습니다.");
    }else{
        s->stack[++s->top]=data;
    }
}

int pop(StackType *s){
    if(is_empty(s)){
        printf("스택이 비어있습니다.");
        return -1;
    }else{
        return s->stack[s->top--];
    }
}
#include <iostream>
#include <string>
using namespace std;
struct Stack {
    int data[10000];
    int size;
    Stack() {
        size = 0;
    }
    void push(int num) {
        data[size] = num;
        size += 1;
    }
    bool empty() {
        if (size == 0) {
            return true;
        } else {
            return false;
        }
    }
    int pop() {
        if (empty()) {
            return -1;
        } else {
            size -= 1;
            return data[size];
        }
    }
    int top() {
        if (empty()) {
            return -1;
        } else {
            return data[size-1];
        }
    }
};
int main() {
    int n;
    cin >> n;

    Stack s;

    while (n--) {
        string cmd;
        cin >> cmd;
        if (cmd == "push") {
            int num;
            cin >> num;
            s.push(num);
        } else if (cmd == "top") {
            cout << (s.empty() ? -1 : s.top()) << '\n';
        } else if (cmd == "size") {
            cout << s.size << '\n';
        } else if (cmd == "empty") {
            cout << s.empty() << '\n';
        } else if (cmd == "pop") {
            cout << (s.empty() ? -1 : s.top()) << '\n';
            if (!s.empty()) {
                s.pop();
            }
        }
    }
    return 0;
}
# 파이썬에서는 스택을 이용할 때 별도의 라이브러리를 사용할 필요 없음.
# 기본 리스트에서 append(), pop() 메서드를 이용하면 스택과 동일하게 동작

stack = []

stack.append(1)
stack.appned(5)
stack.pop()

연결 리스트

  • 장점 : 크기가 제한되지 않는다.
  • 단점 : 구현이 복잡하고 삽입이나 삭제 시간이 오래걸린다.
#include <stdio.h>
#include <stdlib.h>

typedef struct stack{
    int data;
    struct stack * next;
}Stack;

void init(Stack *s);
int is_empty(Stack *s);
int peak(Stack *s);
void push(Stack **,Stack **, int );
void pop(Stack **,Stack **);
#include "stack_list.h"

Node * new_node(int data){
    Node * new = (Node *)malloc(sizeof(Node));
    new->next=NULL;
    new->data = data;
    return new;
}

//스택 초기화
void init(Stack *s){
    s = NULL;
}

int is_empty(Stack *s){
    return (s == NULL);
}

int peak(Stack *s){
    if(is_empty(s)){
        printf("스택이 비어있습니다.");
        return -1;
    }else return s->data;
}

void push(Stack **top, int data){
    Stack * new;
    if(is_empty(*top)){
        new=new_node(data);
    }
    else{
        new = new_node(data);
        new->next = *top;
    }
    *top=new;
}

void pop(Stack **top){
    
    Node * p = *top;
    
    if(is_empty(p)){
        printf("스택이 비어있습니다.\n");
        return ;
    }
    *top = p->next;
    free(p);
}

구현하는 것보다 짜여져 있는 것을 쓰는게 좋다.

#include <iostream>
#include <stack>
#include <string>
using namespace std;


int main ()
{
    stack<int> mystack;
    int n;
    scanf("%d",&n);

    while(n--){
        string ss;
        cin >> ss;

        if(ss=="push"){
            int num;
            scanf("%d",&num);
            mystack.push(num);
        } else if(ss=="top"){
            cout << (mystack.empty() ? -1 : mystack.top())<<"\n";
        } else if(ss=="size"){
            cout << mystack.size()<<"\n";
        } else if(ss=="empty"){
            cout << mystack.empty()<<"\n";
        } else if(ss=="pop"){
            cout << (mystack.empty() ? -1 : mystack.top())<<"\n";
            if(!mystack.empty()){
                mystack.pop();
            }
        }
    }
}

실습

괄호(VPS)

  • 올바른 괄호 문자열의 예시
    • ()
    • (())()
    • ((()))
  • 올바른 괄호 문자열이 아닌 예
    • (()(
    • (()()))
    • (()

스택을 이용해서 괄호 문자열인지 아닌지 알 수 있다.

  1. (가 나오면 스택에 넣는다.
  2. )가 나오면 스택에서 하나를 빼서 (인지 확인한다.

시간복잡도 O(N^2)

=> 스택을 이용해서 O(N)을 O(1)로 줄일 수 있다.

[예시]

  • (())() 스택: (
  • (())() 스택: ((
  • (())() 스택: (
  • (())() 스택:
  • (())() 스택: (
  • (())() 스택:

모든 과정이 끝난 후 스택이 비어있으므로 올바른 괄호 문자열이다. 만약 모든 과정이 끝난 후 스택이 비어있지 않으면 올바른 괄호 문자열이 아니다.

그러므로 스택에 **몇개(size)**가 들어가 있는지가 중요하다!

#include <iostream>
#include <stack>
#include <string>
using namespace std;

string valid(string s){
    int cnt=0;
    for(int i=0;i<=s.size();i++){
        if(s[i]=='('){
            cnt += 1;
        }else if(s[i]==')'){
            cnt -= 1;
        }
        if (cnt < 0) {
            return "NO";
        }
    }
    if (cnt == 0) {
        return "YES";
    }else{
        return "NO";
    }
}
int main(){
    int t;
    cin >> t;

    while(t--){
        string ps;
        cin >> ps;

        cout<<valid(ps)<<"\n";
    }
}

괄호 우선순위

  • 규칙
    1. 대괄호'[]'는 중괄호'{}', 소괄호'()' 안에 올 수 없다.
    2. 중괄호는 소괄호 안에 올 수 없다.
    3. 여는 괄호’(‘,’{‘,’[‘가 나오면 스택에 넣는다.
    4. 닫힌 괄호 ‘)’,’}’,’]’가 나오면 스택에서 뺀다. pop() 이때, 스택의 top이 괄호 짝이 맞아야한다.
    5. 닫힌 괄호가 나왔을 때 스택이 비어있다면 올바른 괄호 문자열이 아니다.
    6. 모든 과정이 끝난 후 스택이 비어있으므로 올바른 괄호 문자열이다. 만약 모든 과정이 끝난 후 스택이 비어있지 않으면 올바른 괄호 문자열이 아니다.
int check(char c,Node **top){
    switch (c) {
        case '(':
            push(top, 2);
            break;
        case '{':
            if(is_empty(*top))push(top, 1);
            else{
                if(peak(*top)==2){
                    printf("[규칙2]실패\n");
                    return -1;
                }
                push(top, 1);
            }
            break;
        case '[':
            if(is_empty(*top))push(top, 0);
            else{
                if(peak(*top)!=0){
                    printf("[규칙1]실패\n");
                    return -1;
                }
                push(top, 0);
            }
            break;
        case ')':
            if(is_empty(*top)){
                printf("[규칙5]실패\n");
                return -1;
            }else if(peak(*top)!=2){
                printf("[규칙4]실패\n");
                return -1;
            }
            pop(top);
            break;
        case '}':
            if(is_empty(*top)){
                printf("[규칙5]실패\n");
            }else if(peak(*top)!=1){
                printf("[규칙4]실패\n");
                return -1;
            }
            pop(top);
            break;
        case ']':
            if(is_empty(*top)){
                printf("[규칙5]실패\n");
            }else if(peak(*top)!=0){
                printf("[규칙4]실패\n");
                return -1;
            }
            pop(top);
            break;
        default:
            printf("잘못 입력 했습니다.\n");
            break;
    }
    return 1;
}

int main(int argc, const char * argv[]) {
    
    Stack * top = NULL;
    int res = 0;
    char c;
    
    printf("값을 입력해주세요. : ");
    while ((c = getchar()) && c != EOF && c!='\n') {
        res = check(c, &top);
        if(res==-1)break;
        if(peak(top)!=-1)printf("스택 top : %c\n",bracket[peak(top)]);
    }
    
    if(res!=-1){
        if (is_empty(top)) {
            printf("\n==괄호 검사 성공==\n");
        }else{
            printf("\n==[규칙6]실패==\n");
        }
    }
}

쇠막대기

  • 레이저는 여는 괄호와 닫는 괄호의 인접한(인덱스 중요) 쌍 ()으로 표현한다. 또한, 모든 ()는 반드시 레이저를 표현한다.
  • 쇠막대기의 왼쪽 끝은 (로, 오른쪽 끝은 닫힌 괄호)로 표현한다.
  1. ()가 나올 때마다 스택에 들어 있는 (의 개수를 세어준다.
  2. )가 나왔을 때는 레이저인지 쇠막대기 인지 구분을 해준다.
  3. 레이저는 항상 붙어진 상태로 나오므로 스택의 (의 인덱스와 1차이가 나는지 확인해야한다.
#include <iostream>
#include <stack>
#include <string>
using namespace std;

int main(){
    stack<int> s;

    int cnt=0;
    string ps;
    cin >> ps;

    for(int i=0;i<=ps.size();i++){
        if(ps[i]=='('){
            s.push(i);
        }else if(ps[i]==')'){
            if(i==s.top()+1){
                s.pop();
                cnt+=s.size();
            }else{
                s.pop();
                cnt+=1;
            }
        }
    }
    cout << cnt << "\n";
}

에디터

  • 커서는 문장의 맨 앞, 맨 뒤, 중간 임의의 곳에 위차할 수 있다.
  • L : 커서를 왼쪽으로 한칸 옮김
  • D : 커서를 오른쪽으로 한칸 옮김
  • B : 커서 왼쪽에 있는 문자를 삭제
  • P $ : $라는 문자를 커서 오른쪽에 추가
  1. 커서를 기준으로 왼쪽 스택과 오른쪽 스택으로 나눠서 문제를 풀 수 있다.
abc|xyz
(|는 커서)
  1. L 왼쪽으로 옮김
ab|cxyz
  1. D 오른쪽으로 옮김
abcx|yz
  1. B 왼쪽 문자 삭제
ab|xyz
  1. P$ $를 커서 왼쪽에 추가하고 커서는 $의 오른쪽에 위치
abcd|xyz

**O(N^2)**에서 스택을 사용하면 **O(N)**으로 시간복잡도가 줄어든다.

#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
char a[600000];
int main() {
    scanf("%s",a);
    stack<char> left, right;
    int n = strlen(a);
    for (int i=0; i<n; i++) {
        left.push(a[i]);
    }
    int m;
    scanf("%d",&m);
    while (m--) {
        char what;
        scanf(" %c",&what);
        if (what == 'L') {
            if (!left.empty()) {
                right.push(left.top());
                left.pop();
            }
        } else if (what == 'D') {
            if (!right.empty()) {
                left.push(right.top());
                right.pop();
            }
        } else if (what == 'B') {
            if (!left.empty()) {
                left.pop();
            }
        } else if (what == 'P') {
            char c;
            scanf(" %c",&c);
            left.push(c);
        }
    }
    while (!left.empty()) {
        right.push(left.top());
        left.pop();
    }
    while (!right.empty()) {
        printf("%c",right.top());
        right.pop();
    }
    printf("\n");
    return 0;
}

후위 표기식

수식의 표기방법

  • 전위 표기법 : 연산자를 피연산자 앞에 표기하는 방법 (+AB)
  • 중위 표기법 : 연산자를 피연산자 중간에 표기하는 방법 (A+B)
  • 후위표기법 : 연산자를 피연산자 뒤에 표기하는 방법 (AB+)

수식을 왼쪽에서 오른쪽으로 스캔하여

  1. 피연산자이면 스택에 저장
  2. 연산자이면 필요한 수만큼의 피연산자를 스택에서 pop
  3. 연산의 결과를 다시 스택에 저장
예제)82/3-32*+
01. push(8) 스택 : 8
02. push(2) 스택 : 8 2
03. second<-pop(2) first<-pop(8) push(first/second) 스택 : 4
05. push(3) 스택 : 4 3
06. second<-pop(3) first<-pop(4) push(first-second) 스택 : 1
07. push(3) 스택 : 1 3
08. push(2) 스택 : 1 3 2
09. second<-pop(2) first<-pop(3) push(first*second) 스택 : 1 6
10. second<-pop(6) first<-pop(1) push(first+second) 스택 : 7

구현시 연산자가 나왔을 때 pop을 두번할 수 있는지와 같은 조건을 따져야한다.

#include <stdio.h>
#include "stack_list.h"

int check(char c,  Stack **top){
    
    int a,b;
    if('0'<=c&& c<='9'){
        push(top, c-'0');
    }else{
        a = peak(*top);
        if(a==-1){
            printf("피연산자의 수가 부족합니다.\n");
            return -1;
        }
        pop(top);
        b = peak(*top);
        if(b==-1){
            printf("피연산자의 수가 부족합니다.\n");
            return -1;
        }
        pop(top);
        
        if(c=='+'){
            push(top, b+a);
        }else if(c=='/'){
            push(top, b/a);
        }else if(c=='*'){
            push(top, b*a);
        }else if(c=='-'){
            push(top, b-a);
        }else{
            push(top, b%a);
        }
    }
    return peak(*top);
}

int main(int argc, const char * argv[]) {
    Stack * head=NULL;
    char c;
    int result=0;
    while ((c = getchar()) && c != EOF && c!='\n') {
        result=check2(c,&head);
        if(result==-1)break;
    }
    if(result!=-1)printf("%d\n",result);
    else printf("실패\n");
    return 0;
}

중위 표기식 → 후위 표기식

  1. 수식의 각 연산자에 대해서 우선순위에 따라 괄호를 사용하여 다시 표현한다. ((A*B)-(C/D))
  2. 각 연산자를 그에 대응하는 오른쪽 괄호의 뒤로 이동시킨다.((A B)* (C D)/)-
  3. 괄호 제거 AB*CD/-

알고리즘 개요

  1. 왼쪽 괄호를 만나면 무시
  2. 피연산자를 만나면 출력
  3. 연산자를 만나면 스택에 삽입
  4. 오른쪽 괄호를 만나면 스택 pop
  5. 수식이 끝나면 스택이 공백이 될 때까지 pop
#include <stdio.h>
#include "stack_array.h"

void convert(char c,StackType *s){
    if(c=='(')return;
    if('0'<=c&&c<='9')printf("%d",c-'0');
    else if(c==')')printf("%c",pop(s));
    else push(s, c);
}

int main(int argc, const char * argv[]) {
    char c;
    Stack s;
    init(&s);
    while ((c = getchar()) && c != EOF) {
        if(c=='\n')break;
        convert(c, &s);
    }
    while((&s)->top!=-1){
        printf("%c",pop(&s));
    }
    
    return 0;
}