2018-08-31.md

2018-08-31

标签（空格分隔）： CASIA

---

翻译

4. 实验

A. 评估指标

我们在类级别和实例级别的分割任务中评估模型的性能。对于类级分割，我们将预测与地面实况标签进行逐点比较，并评估精度，recall和IoU（交叉结合）分数，其定义如下：

$$ \mathcal{P}_{r_c}=\frac{\mid\mathcal{P}_c\bigcap\mathcal{G}_c\mid}{\mid\mathcal{P}_c\mid},\\ recall_c=\frac{\mid\mathcal{P}_c\bigcap\mathcal{G}_c\mid}{\mid\mathcal{G}_c\mid},\\ IoU_c=\frac{\mid\mathcal{P}_c\bigcap\mathcal{G}_c\mid}{\mid\mathcal{P}_c\bigcup\mathcal{G}_c\mid} $$

其中$\mathcal{P}_c$和$\mathcal{G}_c$分别表示属于class-c的预测和地面真实点集。$\mid\cdot\mid$表示集合的基数。IoU评分用作我们实验中的主要准确度指标。

对于实例级分割，我们首先将每个预测的实例-i与地面实例匹配。该索引匹配过程可以表示为 $\mathcal{M}(i)=j$ ， $ i\in\lbrace1,...,N\rbrace$ 是预测实例的索引，$ j\in\lbrace\emptyset,1,...,M\rbrace$ 是地面的真实实例索引。如果没有地面真实与实例i匹配，则 $ \mathcal{M}_i$ 为 $\emptyset$，匹配过程 $\mathcal{M}(\cdot)$ ： 1）按地点数量对地面实例进行排序， 2）对于每个地面实例，找到具有最大IoU的预测实例。评估脚本将与源代码一起发布。

对于每个class-c，我们将实例级精度，recall和IoU分数计算为：

$$ \mathcal{P}{r_c}=\frac{\sum_i\mid\mathcal{P}{i,c}\bigcap\mathcal{G}{\mathcal{M}(i),c}\mid}{\mid\mathcal{P}c\mid},\ recall_c=\frac{\sum_i\mid\mathcal{P}{i,c}\bigcap\mathcal{G}{\mathcal{M}(i),c}\mid}{\mid\mathcal{G}c\mid},\ IoU_c=\frac{\sum_i\mid\mathcal{P}{i,c}\bigcap\mathcal{G}_{\mathcal{M}(i),c}\mid}{\mid\mathcal{P}_c\bigcup\mathcal{G}_c\mid} $$

$ \mathcal{P}{i,c} $ 表示属于class-c的第i个预测实例。不同的实例集互斥，则 $ \sum_i\mid\mathcal{P}{i,c}\mid=\mid\mathcal{P}c\mid$。 对于 $ \mathcal{G}{\mathcal{M}{(i),c}} $ 也同样适用。如果没有地面真实实例与prediction-i匹配，则 $ \mathcal{G}{\mathcal{M}_{(i),c}} $ 就是 $\emptyset$ 。

B. 实验设置

我们的主要数据集是上面描述的转换后的KITTI数据集。 我们将公开可用的原始数据集拆分为具有8,057帧的训练集和具有2,791帧的验证集。 请注意，如果KITTI LiDAR扫描来自同一序列，则它们可以在时间上相关。 在我们的分割中，我们确保训练集中的帧不出现在验证序列中。 我们的培训/验证分组也将发布。 我们在Tensorflow[22]中训练生成了我们的模型，并使用NVIDIA TITAN X GPU进行实验。 由于KITTI数据集仅为前视LiDAR扫描提供可靠的3D边界框，因此我们将水平视野限制为前向90°。 我们的模型训练协议的详细信息将在我们的源代码中发布。

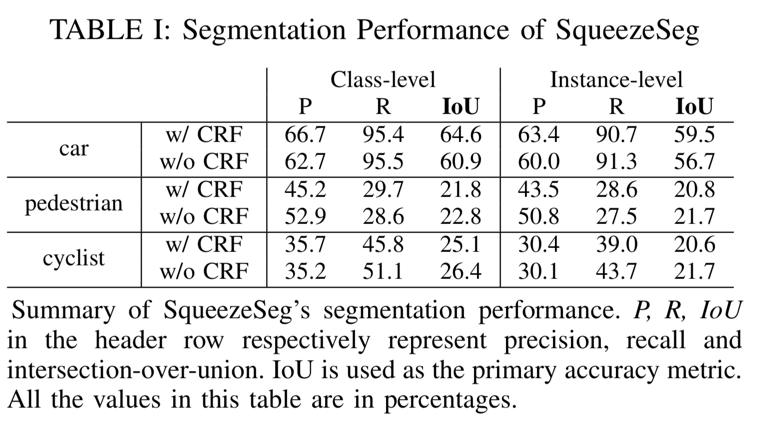
C. 实验结果 SqueezeSeg的分割精度总结在表1中。

我们比较了SqueezeSeg的两种变体，一种是复发CRF层，另一种是没有。尽管我们提出的度量标准非常具有挑战性——因为高IoU需要逐点正确性——SqueezeSeg仍然可以获得高IoU分数，特别是对于汽车类别。请注意，汽车类别的级别级别和实例级别recall都高于90％，这对于自动驾驶来说是理想的，因为假阴性更容易导致事故而不是误报。我们将行人和骑车人类别的较低表现归因于两个原因：1）数据集中的行人和骑车人的实例较少。2）行人和骑车人的实例尺寸要小得多，并且细节更精细，因此更难分割。

通过将我们的CNN与CRF相结合，我们显着提高了汽车类别的准确度（IoU）。性能提升主要来自精度的提高，因为CRF可以更好地过滤边界上错误分类的点。与此同时，我们也注意到CRF导致行人和骑车人分割任务的表现稍差。这可能是由于行人和骑车人缺乏CRF超参数调整。

两个SqueezeSeg模型的运行时间总结在表II中。

TABLE II  <!这是空格＞	Average runtime (ms)	Standard deviation (ms)
SqueezeSeg w/o CRF SqueezeSeg DBSCAN clustering	8.7 13.5 27.3	0.5 0.8 45.8

在TITAN X GPU上，没有CRF的SqueezeSeg仅需要8.7 ms来处理一个LiDAR点云帧。结合CRF层，模型每帧需要13.5 ms。这比目前大多数LiDAR扫描仪的采样率要快得多。例如，Velodyne HDL-64E LiDAR的最大旋转速率为20Hz。在计算资源更加有限的车载嵌入式处理器上，SqueezeSeg可以轻松地在速度和其他实际问题（例如能效或处理器成本）之间进行权衡。另请注意，两个SqueezeSeg模型的运行时标准偏差非常小，这对整个自动驾驶系统的稳定性至关重要。然而，我们的实例分割目前依赖于传统的聚类算法，例如DBSCAN3，相比之下，它需要更长的时间并且具有更大的方差。需要更高效和稳定的集群实现，但这超出了本文的范围。

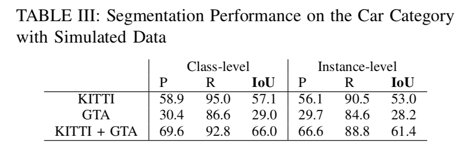
在对GTA模拟数据进行训练时，我们测试了模型在KITTI数据上的准确性——其结果总结在表III中。

我们的GTA模拟器目前仍然有限，无法为行人和骑车人提供逼真的标签，因此我们只考虑汽车的分段性能。此外，我们的模拟点云不包含强度测量值;因此，我们将强度在网络的输入特征中排除。为了量化训练对合成数据的影响，我们在KITTI训练集上训练了SqueezeSeg模型，不使用强度测量，并在KITTI验证集上进行了验证。模型的性能显示在表格的第一行。与Table.I相比，由于强度通道的损失，IoU得分更差。如果我们在GTA模拟数据上完全训练模型，我们会发现性能明显更差。然而，将KITTI训练集与我们的GTA模拟数据集相结合，我们发现显着提高的准确度甚至比Table.I更好。

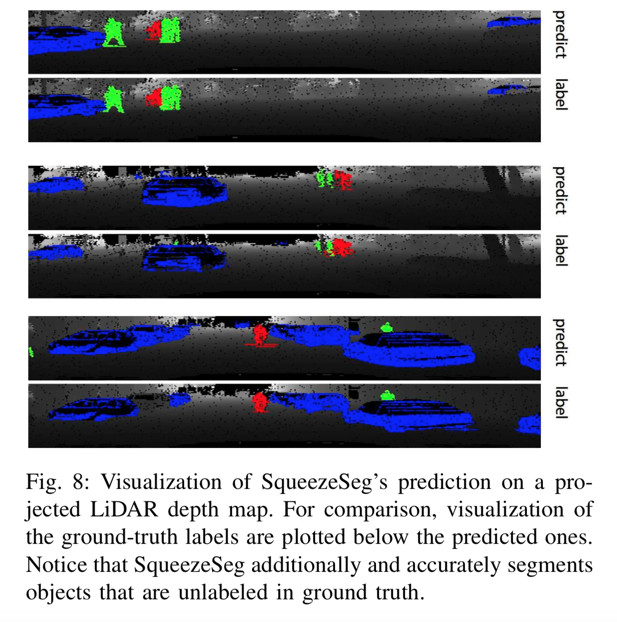
SqueezeSeg与地面实况标签的分割结果可视化可以在图8中看到。

SqueezeSeg与地面实况标签的分割结果可视化可以在图8中找到。对于大多数物体，预测结果几乎与地面实况相同，除了目标物体下方的地面。另外请注意SqueezeSeg，并准确地分割在地面实况中未标记的对象。这些物体可能被遮挡或太小，因此被置于KITTI基准的“不关心”类别中。

5. 总结

我们提出了SqueezeSeg，一种准确，快速和稳定的端到端方法，用于从LiDAR点云进行道路对象分割。为解决引言中讨论的先前方法的不足，我们的深度学习方法1）不依赖于手工制作的功能，而是利用通过培训学到的卷积滤波器; 2）使用深度神经网络，因此不依赖于迭代算法，如RANSAC，GP-INSAC和凝聚聚类; 3）将管道减少到一个阶段，回避传播错误的问题，并允许模型充分利用对象上下文。该模型以快于实时的推理速度实现非常高的精度，并且具有小的方差，如自动驾驶等应用所需。此外，我们综合了大量的模拟数据，然后在使用合成数据进行训练并验证真实数据时，表现出显着的性能提升。我们使用选择类作为概念验证，授予合成数据在未来自动驾驶数据集中的潜在作用。

致谢

这项工作部分得到了DARPA PER- FECT计划，奖项HR0011-12-2-0016，以及ASPIRE实验室赞助商英特尔，以及实验室附属公司HP，华为，Nvidia和SK海力士的支持。 这项工作也得到了宝马，英特尔和三星全球研究组织的个人礼物的部分赞助。

PS

联合概率、边际概率、联合概率

	x1	x2	x3	x4	$ P_y(Y)\downarrow $
y1	$\frac4{32}$	$\frac2{32}$	$\frac1{32}$	$\frac1{32}$	$\frac8{32}$
y2	$\frac2{32}$	$\frac4{32}$	$\frac1{32}$	$\frac1{32}$	$\frac8{32}$
y3	$\frac2{32}$	$\frac2{32}$	$\frac2{32}$	$\frac2{32}$	$\frac8{32}$
y4	$\frac8{32}$	0	0	0	$\frac8{32}$
$ P_x(X)\rightarrow $	$\frac{16}{32}$	$\frac8{32}$	$\frac4{32}$	$\frac4{32}$	$\frac{32}{32}$

$$ 人生事件决策函数Life（time）=\lim_{time\to+now}\max\lbrace{You(want)}\rbrace $$