diff --git a/data-science-notes/k-means b/data-science-notes/k-means
new file mode 100644
index 00000000..c2e9d682
--- /dev/null
+++ b/data-science-notes/k-means
@@ -0,0 +1,54 @@
+# K-means Clustering
+
+This is a classic clustering algorithm that relies on the concept of centroids and their Euclidean distances from the observed data points. The basic concept works on the following set of rules:
+
+1. Assign a fixed number of centroids randomly in the parameter space (the number of centroids will define the number of clusters formed at the end of execution of the algorithm). These centroids need not be one of the points in the observation set, and can literally be random coordinates in the multi-dimensional space that we have.
+2. Calculate the closest centroid from each data point in the observation set and assign the data point to that centroid's cluster.
+3. Move the centroid to the 'center-of-mass' of the cluster that it has created with help of our data points from observation set.
+4. Repeat **Step 2** and see if any points have changed their clusters, from the ones they were previously assigned. If the condition holds true then move to **Step 3** otherwise proceed to **Step 5**.
+5. Finish
+
+Although, the algorithm might appear like its' construction of clusters based on the distances, this assumptions is untrue. The **k-means clustering algorithm works primarily on minimizing the intra-cluster variance** and that is the reason why metric of computation for accuracy of a k-means cluster is WCSS (within-cluster sum of squares).
+
+#### Objective Function for Soft K-means
+
+The objective function for K-means clustering is given by:
+
+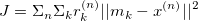
+
+This equation is the sum of squared distances weighted by the responsibilities. This means that if 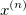 is far away from cluster 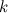, that responsibility should be very low. This is an example of coordinate descent, which means that we are moving in the direction of a smaller *J* with respect to only one variable at a time. As we have already established, although with each iteration, we converge towards a smaller J, there is absolutely no guarantee that it will converge to a global minimum.
+
+> It is interesting to observe that the k-means clustering algorithm relies on Euclidean distances for formation of clusters and computation of intra-cluster variation. This is an implicit underlying bias of the algorithm and can be exploited for other kinds of correlations between the attributes by transforming them into Euclidean distances. [Click here](https://stats.stackexchange.com/questions/81481/why-does-k-means-clustering-algorithm-use-only-euclidean-distance-metric/81494#81494) for a more detailed explanation regarding this.
+
+**Drawbacks**: As it should be already obvious at this point, the selection of random points could cause serious problems because this randomness would let the algorithm to figure out different clusters than the ones that are actually present in the hyper-dimensional space. This sensitivity to initialization can be alleviated to some extent by the use of following techniques:
+
+1. Run the algorithm multiple times and choose the centroids that give us the best cost
+2. Soft K-means algorithm: This allows for each point to be assigned to more than one cluster at a time, allowing for a probability distribution over the centroids.
+3. K-means++ algorithm:
+
+#### Soft K-means algorithm
+The Soft K-means algorithm works as follows:
+
+1. initialize m1 ... mx as random points
+2. Calculate cluster responsibilities using 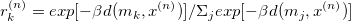
+3. Calculate new means using 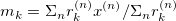
+4. If converged, goto **Step 5**, else goto **Step 2**
+5. Finish
+
+
+## RESEARCH ARTICLES
+
+1. **K-Means++: The advantages of careful seeding**; [David Arthur, Sergei Vassilvitskii](http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf)
+
+ **[Solved]** The random selection of centroids would often let the k-means algorithm figure out different clusters than the ones that are actually present in the hyper-dimensional space.
+
+ This algorithm selects only the first centroid at random and then picks the remaining centroids by using a probability distribution function over the data points. (**Section 2.2**)
+
+2. **A comparative study between fuzzy clustering algorithm and Hard Clustering algorithm**; [Dibya Joti Bora, Dr. Anil Kumar Gupta](https://arxiv.org/ftp/arxiv/papers/1404/1404.6059.pdf)
+
+ **[Solved]** Sensitivity to random start of K-means has been alleviated to some extent using fuzzy clustering. Any point does not fully belong to one cluster and there's a probability of over the asignment of any point to a cluaster.
+
+
+## CODE REFERENCES
+
+Read the [documentation](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html) for more