Vid övningen ska du vara beredd att muntligt presentera och diskutera dina lösningar och din programkod.
- Gör (minst) en fil per uppgift och lägg filerna i katalogen
username-ovn5i organisationen grudat21 på KTH GitHub. - Utgå från mallarna i /grudat21/ovn0/.
- Lösningar ska vara inlämnade före deadline.
Grafer 101 (video)
- Rita alla enkla sammanhängande grafer med hörnen 1, 2, 3, 4, där samliga hörn har gradtal 1.
- Rita alla enkla sammanhängande grafer med hörnen 1, 2, 3, 4, där samliga hörn har gradtal 2.
- Rita alla enkla sammanhängande grafer med hörnen 1, 2, 3, 4, där samliga hörn har gradtal 3.
- Hur många kanter kan det som mest finnas i en graf med n stycken hörn?
- Hur många kanter kan det som mest finnas i en enkel graf med n stycken hörn?
- Hur många kanter kan det som mest finnas i ett träd med n stycken hörn?
Motivera dina svar.
-
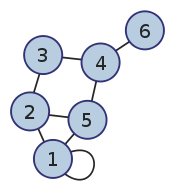
Besök noderna i den här grafen i DFS- och BFS-ordning med start i nod 1. I vilken ordning besöks noderna i de två fallen? Du kan anta att grannarna till en nod besöks i nummerordning.
-
Tidskomplexiteten för DFS blir i vissa fall mycket bättre om man använder närhetslistor i stället för en närhetsmatris. Varför då?
-
För vilken typ av grafer blir den asymptotiska tidskomplexiteten för DFS den samma för båda datastrukturerna?
En plikttrogen lärare vill dela ut uppgifter till sina elever så att inga som känner varandra får samma uppgift. Läraren är optimist – och dessutom lite lat – så han tror att det räcker med två uppgifter. Designa en algoritm som testar om det stämmer.
Modellera problemet med en graf där varje hörn motsvarar en elev. Grafen har kanter mellan de hörn som motsvarar elever som känner varandra. Algoritmen ska baseras på en metodisk genomgång av grafen med BFS eller DFS.
- Beskriv din algoritm i pseudokod.
- Beräkna också tidskomplexiteten.