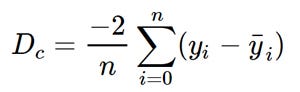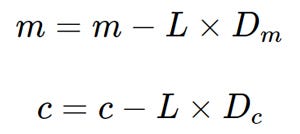This program is all about implementing Linear Regression using Gradient Descent
Linear Regression is used to model relationship between dependent and one or more Independent variable. The variables must have continous values.
The equation of line is Y = m * X + c
our predicted value is given by : y = m * x + c + ε ; where ε is the error while predicting the value.
Our motive is to minimize the cost function while predicting the values
The cost function is given by:
J(m,c) = (1/n) Σ (Y - Y_pred)^2
J(m,c) = (1/n) Σ (Y - (m * x + c))^2
The algorithm we use to minimize the cost function is known as Gradient Descent Algorithm. It involoes three important steps:-
- Start with a given value v
- Iterate:
- v(i+1) = v(i) + a * f'(v) [here,a is the learning rate]
- Stop after some condition is matched.
To minimize the cost function we need to partial derivate the cost function in terms of m and c, thus we get
At each step we need to update the value of m and c. The formula for upgradation is
We continue the process until out loss function is quite small or ideally zero.