-
Notifications
You must be signed in to change notification settings - Fork 5
Mesh Voxelization
Voxlization is the process of creating 3D volumes of geometric models either from their parametric representations or from polygonal or polyhedral, tetrahedral and hexahedral meshes. Voxelization is classified into two categories: surface and solid voxelization. Surface voxelization creates volumetric shells representing boundaries of surface manifolds as a series of connected voxels - generally if no holes exist on the surface, while solid voxelization fills their interiors1.
We implemented a data-parallel fast surface voxelization algorithm, which sets all the voxels that overlap with any triangle in a given mesh using conservative rasterization2. In contrary to standard rasterization, the conservative criterion guarantees that a voxel is filled if it is {partially} overlapping or even {touching} a triangle. The algorithm can reconstruct a volumetric shell corresponding to the extent of a given triangle soup, even in the presence of self-intersecting triangles, non-manifold edges and non-manifold vertices. The bounding box of each voxel is computed from its three-dimensional index and side length. For every triangle in the mesh, a box-triangle intersection test is performed to rasterize all the polygons in the mesh and create a volumetric shell that reflects the surface of the mesh. Note that all the n-gons (n > 3) in the input mesh are automatically split into triangles prior to voxelization.
Figure 1 shows a projection of a volume that is created using surface voxelization only for an input neuron mesh.

Figure 1
Conventional solid voxelization algorithms in computer graphics require a watertight manifold to successfully voxelize its interior into occupancy grids. By definition, a watertight mesh consists of a compact manifold that has clearly defined inside and does not contain any holes across its surface; that is if the surface is punctured with a hypodermic needle trying to fill it with water, it will not leak. A triangular mesh is guaranteed to be watertight - if and only if - it has no self-intersecting triangles, zero non-manifold edges, zero non-manifold vertices, and no boundary edges. In reality, and unfortunately, neuroscientific mesh models segmented from microscopy stacks have ill topologies with hundreds or even thousands of self-intersections, non-manifold edges and vertices and even fragmented mesh partitions. Major contributions have been introduced to fix the topology of these meshes using geometric mesh conditioning, nevertheless, their solutions are neither robust nor scalable, based on trials. Therefore, existing solid voxelization algorithms would fail to handle detailed mesh reconstructions with realistic geometries. Contrary to traditional methods, we present an efficient data-parallel, slice-based solid voxelization algorithm that does not entail an input watertight mesh. Initially, the surface voxelization algorithm converts a given triangular mesh into a volumetric shell in a uniformly sampled 3D Cartesian grid. The rasterization is binary, where each voxel in the grid is either set or cleared. The interior of the shell can be filled using 3D flood-filling. However, this algorithm is accompanied with extensive computational loads and cannot be easily parallelized. Our algorithm is based on 2D flood-filling that can be implemented in parallel. The 2D flood-filling kernel is applied independently to each slice in the volume. The aggregate result is exactly similar to what can be accomplished with 3D flood-filling, but in much less time. Our implementation is based on a previous algorithm that was used to reconstruct large scale volumes of neocortical circuits from input morphological skeletons3. Figure 2 shows a projection of a volume that is created using solid voxelization after rasterizing the input neuron mesh as shown in Figure 1.
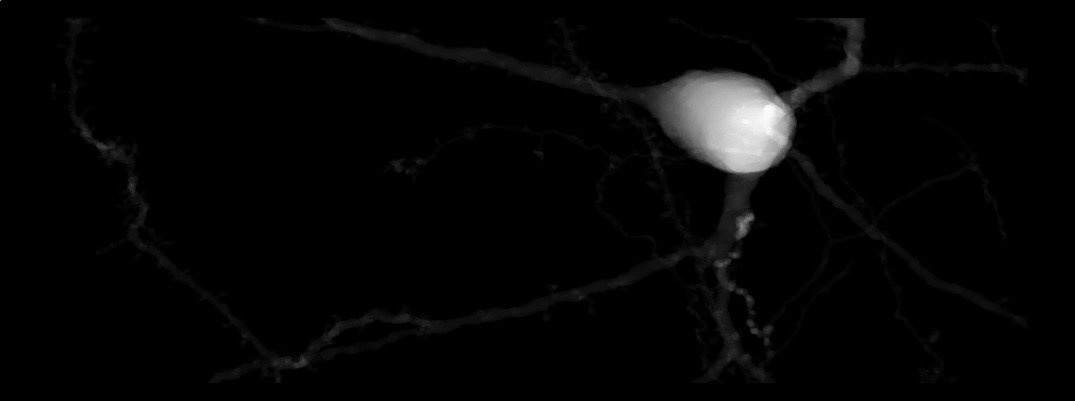
Figure 2
By default, the solid voxelization algorithm is applied on a per-slice-basis along the Z-axis of a given volume grid, where each slice is processed, or flood-filled, in a separate thread, independently. Certain structures, for example vascular morphologies - represented with cyclic graphs - have loops. In the general case, the flood-filling algorithm is unable to identify any internal boundaries beyond the first one detected. Therefore, running the flood-filling kernel along a single axis will fail to capture the entire geometry of an input mesh. To resolve this constraint, we implemented a 3-way solid voxelization algorithm which processes the volume along the X, Y and Z axes to produce three volume grids that are combined later with a logical ANDing operation to obtain the final grid. This approach makes it possible to resolves all the loops in a given cyclic structure.
The following core applications use voxelization in their workflows to either construct an intermediat volume that can be used later to reconstruct the final mesh or generate an output volume that can be loaded with volume visualization applications:
- ultraMesh2Mesh (intermediate data)
- ultraMeshes2Mesh (intermediate data)
- ultraNeuroMorpho2Mesh (intermediate data)
- ultraAstroMorpho2Mesh (intermediate data)
- ultraVessMorpho2Mesh (intermediate data)
- ultraMesh2Volume (principal output)
Automatically, surface voxelization is used to create a volume shell from the input data (either mesh or a morphology). Solid voxelization is taken into consideration if the --solid argument is added to the command line. By default, the voxelization-axis used to implement the solid voxelization algorithm is the z axis.
The user can select which voxelization axis the solid voxelization kernel is applied using the voxelization-axis argument. The values are either x, y, z or xyz for 3-way solid voxelization.
If the input dataset (mesh or morphology) has a loop, the 3-way solid voxelization is essential to guarantee the reconstruction of a correct output mesh.
Users can select to voxelize the input dataset (mesh or morphology) either with a fixed resolution value or based on its dimensions.
By default, a 512 fixed resolution is used. Typically, volume resolution is defined by three values along the XYZ axes. For simplicity, we use a single value (called base resolution) with which we can define the resolution along the three axes. This base resolution corresponds to the largest dimension of the input dataset as computed from its bounding box. For example, if the input dataset has a bounxing box of 100 x 200 x 300 micron, and if the default 512 volume resolution is used, then volume resolution will be computed as follows:
- z-resolution = 512
- y-resolution = 200 / 300 * 512 = 341
- x-resolution = 100 / 300 * 512 = 171
So the final volume resolution will be 171 x 341 x 512.
In certain cases, users wish to maintain the sampling density along the volume. In this case, we can define the resolution of the volume based on the dimensions of the input dataset (mesh or morphology). To enable this option, use the --scaled-resolution flag and the voxels-per-micron arguments to define the scale. For traditional reasons, the input dataset (mesh or morphology) is assumed to be defined with microns units. For example, if the bounding volume of the input dataset is computed to be 120 x 130 x 150, the units are assumed to be cubic microns. Therefore if the --voxels-per-microns value is set to 1, the resolution of the volume will be 120 x 130 x 150, and if the value is 2, the resolution will be 240 x 260 x 300. This option is used to avoid any scaling issues if multiple datasets are later combined together into a single, yet multi-partitioned, model for some simulation.
Note that if the coordinates of the input models are defined in the nano-meter resolution scale, the volume resolution will potentially result in segmentation fault if the
voxels-per-micronvalues are in their typical range. Therefore, the input datasets must be scaled up to have micron-scale coordinates.
An input non-watertight neuron mesh is processed with ultraMesh2Mesh to reconstruct a watertight output. We used the --scaled-resolution option and values of 1, 3, 5 and 10 for the --voxels-per-micron option. The results are shown in the following table:
| Voxels Per Micron | Surface Voxelization |
|---|---|
| 1 |  |
| 3 |  |
| 5 |  |
| 10 |  |
-
Schwarz, Michael, and Hans-Peter Seidel. Fast parallel surface and solid voxelization on GPUs. ACM transactions on graphics (TOG) 29.6 (2010): 1-10.
-
Hasselgren, J., Akenine-Möller, T., & Ohlsson, L. (2005). Conservative rasterization. In GPU Gems 2 (pp. 677-690). Addison-Wesley.
-
Abdellah, Marwan, et al. Reconstruction and visualization of large-scale volumetric models of neocortical circuits for physically-plausible in silico optical studies. BMC bioinformatics 18.10 (2017): 39-50.