CMP3103 Week 4
Besides the following tasks, make sure you have caught up with all the previous tasks.
IMPORTANT: You are expected to bring your source code from the previous workshop(s) to every workshop again. Also you are expected to take your own notes, e.g. about the commands you use, how things worked, etc, and have them available for every session. The workshops are successively building on top of each other. You need the knowledge from the previous workshops to engage in this one. It is strongly advised to store all your coding after every session. Best recommendation for this to use a source code repository, free to use from various providers, such as http://github.com or https://bitbucket.org/, for instance.
In the lecture the robot kinematics (internal kinematics, external kinematics, direct kinematics, and inverse kinematics) for a robot with a differential drive (like the turtlebot) have been introduced.
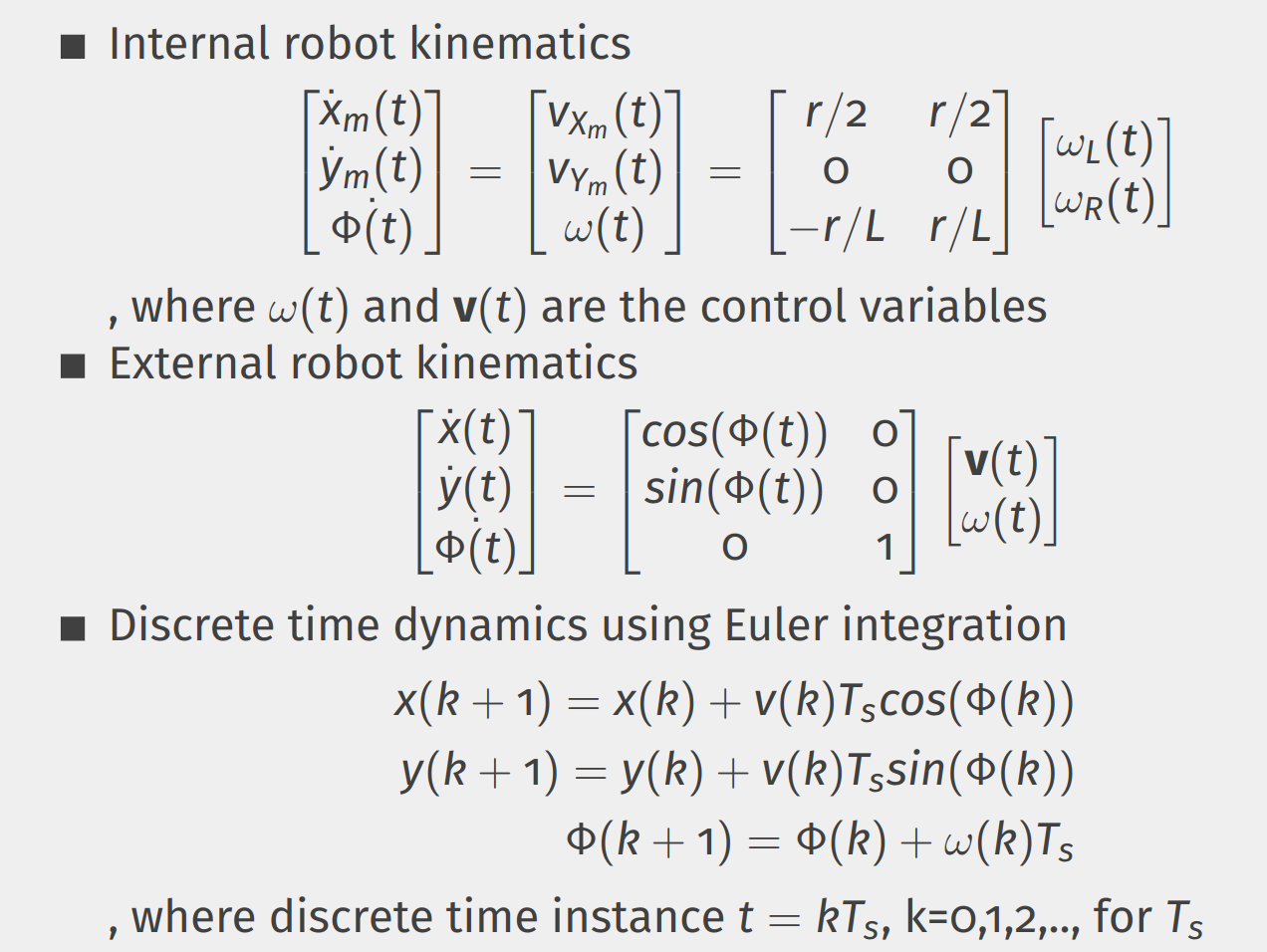
You already know that your turtlebot accepts a geometry_msgs/Twist message on the topic /cmd_vel to receive motion commands. This Twist message defines the linear velocity and the angular velocity, which the turtlebot driver converts into angular velocities ω using the "inverse kinematics".
However, assume you want to command your robot using wheel angular velocity yourself, so, you want to define the angular velocities ω for each wheel. Then, you need to use the forward kinematics to find the values for a suitable Twist message from given ω values.
Let's try to control a differential drive robot. Consider you are given the following vehicle parameters: sampling period self.robot_current_pose
- v(t) = 0.5 m/s,
$\omega(t)$ = 0 rad/s - v(t) = 1 m/s,
$\omega(t)$ = 2 rad/s - v(t) = 0 m/s,
$\omega(t)$ = 2 rad/s - wheels angular velocities are
$\omega(t)_L= 20 rad/s$ and$\omega(t)_R= 18 rad/s$