An analysis on the threaded C implementation of
the Discrete Cosine Transform (DCT)
[Discrete Cosine Transform]
[Acknowledgements]
[Issues]
This project is my submission for the final project in CSCI-551, Parallel Programming and Numerical Methods, as California State University, Chico.
It serves as an implementation of multithreading the Discrete Cosine Transform (DCT) algorithm; as well as an analysis into how well that implementation performed under rigerous testing and observation. This anaylsis is oriented towards the questions required by the assignment, and is by no means or method a full anaylsis into the algorithm or my implementation of it. However, it does cover basics such as how well it scales, it's performance with regards to Amdahl's law, etc.
This report has been uploaded with the permission of the professor when I had originally made it, if there are any issues please feel free to contact me.
Step-1: Obtaining Source Input
The first step is to obtain the source image by whatever means is desired (e.g. generation of a new image or reading in an old one).
An image is defined as follows,
// Pixel structure definition
// --------------------------
//
// r : Value of intensity of 'red' of this pixel
// g : Value of intensity of 'green' of this pixel
// b : Value of intensity of 'blue' of this pixel
// i : Value of grayscale intensity of this pixel
//
typedef struct {
valueType r, g, b;
valueType i;
} pixel;
// Image structure definition
// --------------------------
//
// width : Amount of pixels in the x-direction
// height : Amount of pixels in the y-direction
// m : The matrix itself containing all pixels
//
typedef struct {
int width;
int height;
int channels;
pixel** m;
} image;After getting that image, you may or may not need to 'pad' the bottom border of it to accomodate the amount of threads that you're using.
This is because each thread processes it's portion of the image in 8 x 8 macroblocks, which helps with accuracy and percision.
Once each of the settings are calculated or fed in, we now need to make 2 other images to hold both the DCT and IDCT image results.
Step-2: Threading Setup
Once you have your source image loaded in, the program then has to calculate how to split the work of iterating over the source image for the amount of threads it's using. This is because the threads all work on different horizontally sliced sections of the image in 8 x 8 macroblocks.
e.g. For a 32x32 size image using 2 threads
Thread 1
Total Area Assigned: Rows 0-15, Columns 0-31
-> Macroblocks: image[ 0-7][0-7], image[ 0-7][8-15], image[ 0-7][16-23], image[ 0-7][24-31],
image[ 8-15][0-7], image[ 8-15][8-15], image[ 8-15][16-23], image[ 8-15][24-31]
Thread 2
Total Area Assigned: Rows 16-31, Columns 0-31
-> Macroblocks: image[16-23][0-7], image[16-23][8-15], image[16-23][16-23], image[16-23][23-31],
image[24-31][0-7], image[24-31][8-15], image[24-31][16-23], image[24-31][24-31]
These macroblocks are used because the DCT algorithm involves calculating using a summation which, given that it uses things like cos() and M_PI, involves some level of innaccuracy. To minimize that issue, each thread utilizes the sum of each 8 x 8 area to calculate the DCT & IDCT values of each pixel lying inside that area rather than relying on the sum of the entire image.
Step-3: Threading Runtime
This is where a majority of the work happens.
In this step, each thread must work within 8 x 8 blocks of it's assigned area of the image to calculate both the DCT values and IDCT values for the pixels inside the 8 x 8 macroblocks. As each DCT and IDCT value for a pixel is calculated, it also assigns those values to the corrosponding DCT/IDCT images it was passed in the arguments. As you can see below, the functions imBlockDCT & imBlockIDCT() are called on the beginning of each 8 x 8 macroblock, where upon they calculate the values for each pixel in the entire 8 x 8 macroblock for their corrosponding process.
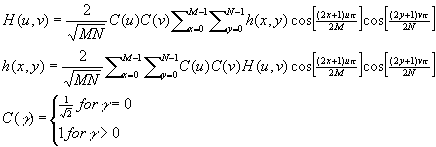
void imBlockDCT(image* inIMG, image* outIMG, int i, int j) {
double OOSQT = 1.0/sqrt(2.0);
double sum = 0.0;
double HPW = (double)16.0;
for (int u = 0; u < 8; u++) {
for (int v = 0; v < 8; v++) {
sum = 0.0;
for (int x = 0; x < 8; x++) {
for (int y = 0; y < 8; y++) {
sum += (double)inIMG->m[i + x][j + y].i *
cos(((2.0*(double)(x)+1.0) * (double)u * M_PI)/HPW) *
cos(((2.0*(double)(y)+1.0) * (double)v * M_PI)/HPW);
}
}
outIMG->m[i + u][j + v].i = 0.25
* (u == 0? OOSQT:1.0)
* (v == 0? OOSQT:1.0)
* sum;
}
}
}void imBlockIDCT(image* inIMG, image* outIMG, int i, int j) {
double OOSQT = 1.0/sqrt(2.0);
double sum = 0.0;
double MPOL = M_PI/(double)16.0;
for (int x = 0; x < 8; x++) {
for (int y = 0; y < 8; y++) {
sum = 0.0;
for (int u = 0; u < 8; u++) {
for (int v = 0; v < 8; v++) {
sum += inIMG->m[i + u][j + v].i *
(u == 0? OOSQT:1.0) *
(v == 0? OOSQT:1.0) *
cos((2.0*(double)(x)+1.0) * (double)u * MPOL) *
cos((2.0*(double)(y)+1.0) * (double)v * MPOL);
}
}
outIMG->m[i + x][j + y].i = sum * 0.25;
}
}
}Step-4: Collecting & Verifying Results
Now we need to verify the values for each of the images (DCT & IDCT) that we've calculated.
To do so, we call imValidate(), which iterates over the values of each pixel in both the source and IDCT images.
What it does for each pixel is ask if the pixels are the same within a certain amount of precision.
On the basis that I use double for my process and to hold the values of each pixel, I would expect that for pixel values in the range of [0.0,255.0] that there would be only 12 digits of precision at worst. As such, I set the imValidate() to check that there is it least that level of 'similarity' between the input image and the calculated output of IDCT.
After that, to confirm the level of error I use both imMSE() and the imERR() functions.
The imMSE() performs the Mean-Squared-Error calculation for my two images, and the imERR() functions calculate the basic |Source - IDCT|/TotalPixels value for average error per pixel.

long double imMSE(image* imA, image* imB) {
image* imC = allocateImage(imA->width,
imA->height,
imA->channels);
long double MSE = (long double)0.0;
for (int y = 0; y < imA->height; y++) {
for (int x = 0; x < imA->width; x++) {
MSE += pow((long double)(imB->m[x][y].i - imA->m[x][y].i),
(long double)2.0);
}
}
return (MSE / (long double)(imA->height * imA->width));
}double imERR1(image* imA, image* imB) {
double avg_err = 0.0;
for (int y = 0; y < imA->height; y++) {
for (int x = 0; x < imA->width; x++) {
avg_err += fabs(imB->m[x][y].i - imA->m[x][y].i)/imA->m[x][y].i;
}
}
return avg_err;
}Precision
This was one of the two biggest questions, "How precise was your process?" What I did to figure this was look at the results of testing using randomly generated images,
Original Image:
[ 49.000] [ 143.000] [ 154.000] [ 122.000] [ 195.000] [ 130.000] [ 148.000] [ 24.000]
[ 108.000] [ 107.000] [ 54.000] [ 64.000] [ 242.000] [ 246.000] [ 73.000] [ 167.000]
[ 174.000] [ 207.000] [ 28.000] [ 120.000] [ 89.000] [ 87.000] [ 150.000] [ 205.000]
[ 104.000] [ 82.000] [ 77.000] [ 120.000] [ 200.000] [ 249.000] [ 96.000] [ 121.000]
[ 9.000] [ 250.000] [ 243.000] [ 204.000] [ 253.000] [ 9.000] [ 100.000] [ 233.000]
[ 116.000] [ 155.000] [ 170.000] [ 230.000] [ 18.000] [ 243.000] [ 142.000] [ 64.000]
[ 68.000] [ 42.000] [ 57.000] [ 29.000] [ 1.000] [ 207.000] [ 234.000] [ 106.000]
[ 34.000] [ 56.000] [ 98.000] [ 106.000] [ 177.000] [ 194.000] [ 227.000] [ 186.000]
DCT Image:
[1049.500] [-149.537] [ -67.955] [ 40.747] [ -65.000] [ -64.563] [ -21.642] [ -42.673]
[ 10.651] [ 96.141] [ -33.225] [ 50.615] [ 81.797] [-120.872] [ -29.143] [ 30.648]
[ -76.726] [ -99.670] [ -2.712] [ 103.694] [ -69.179] [ 56.328] [ 11.108] [ 52.924]
[ 10.731] [ 114.142] [-112.968] [ -93.274] [ -95.186] [ 45.639] [ 0.669] [ -4.690]
[ 48.750] [ -10.624] [-140.618] [ -89.078] [ 35.250] [ -74.794] [ -44.852] [ 116.873]
[-105.789] [ -10.778] [ 50.536] [ 105.910] [ -81.370] [ 119.240] [ 19.944] [ -32.342]
[ 43.417] [ 93.648] [ 20.358] [ -57.351] [ -15.452] [ 80.069] [ -55.038] [ -63.178]
[ -2.803] [ 29.420] [ 91.698] [-163.144] [ 21.393] [ -35.917] [-128.542] [ 70.893]
IDCT Image:
[ 49.000] [ 143.000] [ 154.000] [ 122.000] [ 195.000] [ 130.000] [ 148.000] [ 24.000]
[ 108.000] [ 107.000] [ 54.000] [ 64.000] [ 242.000] [ 246.000] [ 73.000] [ 167.000]
[ 174.000] [ 207.000] [ 28.000] [ 120.000] [ 89.000] [ 87.000] [ 150.000] [ 205.000]
[ 104.000] [ 82.000] [ 77.000] [ 120.000] [ 200.000] [ 249.000] [ 96.000] [ 121.000]
[ 9.000] [ 250.000] [ 243.000] [ 204.000] [ 253.000] [ 9.000] [ 100.000] [ 233.000]
[ 116.000] [ 155.000] [ 170.000] [ 230.000] [ 18.000] [ 243.000] [ 142.000] [ 64.000]
[ 68.000] [ 42.000] [ 57.000] [ 29.000] [ 1.000] [ 207.000] [ 234.000] [ 106.000]
[ 34.000] [ 56.000] [ 98.000] [ 106.000] [ 177.000] [ 194.000] [ 227.000] [ 186.000]
imValidate() return value: 0
imERR1() return value: 0.0000000000001040928649761
imERR2() return value: 0.0000000000000216649524005
imMSE() return value: 1.616267526423385e-26
What's important to note is imERR1() returned a value that tells us that on average, we saw numbers would only start to differ after the 12th decimal point. When thinking about the fact that the we're generating values [0,255] for each pixel and that the process uses double, the reason for this becomes clear:
- Since the range is significantly more filled with three digit numbers, we can assume the average pixel's value is in the three digit range
[100,255] - Using
double, you have up to 15 total decimal places of precision
With that said, you would see that the error for an average numbers occurs after the 12th decimal point because the average number already has 3 digits of precision taken up already.
To confirm this was the result, I tried varying size images and threads to see if this changed. However, as you can see my initial hypothesis was correct:
Height: 1440
Width: 2560
Bits: 8
Channels: 1
Total Threads: 8
imValidate() return value: 0
imERR1() return value: 0.0000000068655844276073249
imERR2() return value: 0.0000000000000000000000000
imMSE() return value: 1.440301205049921e-26
Speed
To accomplish this, I made an alternate testing/driver file to repeatedly perform the process of:
Generate random imageStart timerPeform DCT/IDCTStop timerCalculate the error
To ensure I had a rich set of data to show, I choose to then perform this process using [1-10] threads and average the result of performing it 25 times for each thread data point.
To make sure the data was not influenced by any other processes trying to run at the same time, I performed these tests on a new Google Cloud Compute Engine instance with minimal background processes. Below are the graphs for average time required and the speedup versus what is expected with respect to Amdahl's Law.


What you can observe here is that there was an extremely efficient speedup of the process using threads. For instance, with a random image of size 2560 x 1440 we saw that using only 1 thread to calculate it took on average 33.20 seconds, whereas using 8 took 4.955 seconds on average.
Additionally, we can also observe that it follows Amdahl's law to some degree. Looking at the plot, we can see that the RMSE of the speedup observed versus the expected speedup with respect to Amdah's law is 0.3766. Finally, from this plot we can also calculate that there was 96% code parallelism given Amdahl's law.
TC-DCT was originally meant as a school project. As such, it is heavily commented and there may be certain sections with verbose documentation.
