implement "nearly division less" algorithm for rand(a:b)

[rfourquet]

Cf. https://arxiv.org/abs/1805.10941.
Closes #20582, #29004.

This is still about 30 percent slower than the "biased" solution (e.g. #28987), but as fast as the "best case" of the current version (when the range length is a power of 2). So this is strictly better, and should become the default version in a future (major) release. How do we make this available in the meantime? rand(Random.fast(a:b)) is what the PR currently implements.

[rfourquet]

cc @affans

[StefanKarpinski]

Can't the behavior of rand(a:b) just be changed to use this without breaking the API?

[KristofferC]

Presumably, it changes what random numbers are generated.

[tkluck]

Arguably, it's only breaking API for those cases where the code uses seed!. So one way of preserving the API is as follows: in the new version of Julia, we set a default seed to something like seed!(FasterRandom(<some seed>)). If the user uses seed!(::Integer), that's our cue to use the slower (but api-stable) random number generator from that point onwards.

[GregPlowman]

Just saw a reference to this on Discourse.
Could it be implemented now as Future.rand()?

[stevengj]

See also the discussion in #30494 — I'm skeptical that we should guarantee that the exact sequence of random number for a given seed is a stable part of the API.

[rfourquet]

See also the discussion in #30494 — I'm skeptical that we should guarantee that the exact sequence of random number for a given seed is a stable part of the API.

I agree that that PR set a precedent, i.e. implicitly a rule that changing the stream of generated number is considered as "minor change". Should this be triaged to confirm?

Note though that we use a lot of Random.seed!(123) in tests, so changing the streams in a minor release means that some people would have to update their tests. Also, a change of streams between 0.6 and 0.7 was sufficiantly annoying to a user that he made a compatibility package to reproduce the 0.6 streams on 0.7+.

PS: I rushed a lot of PRs before the release of Julia 1 only because I was under the belief that we would guarantee the reproducibility of streams, I'm pretty sure this idea was in the air somehow... but it was for the best I guess!

[halleysfifthinc]

Suggested change

	# up to 64 bits. This will be the default in a future realease.
	# up to 64 bits. This will be the default in a future release.

[stevengj]

People generally set Random.seed in tests not because they care about the exact sequence of random numbers but because they don’t want tests to fail on rare occasions when something extremely improbable occurs (e.g. a random matrix happens to be nearly singular, exacerbating roundoff errors). By the same token, however, such tests are extremely unlikely to fail if we change the pseudorandom stream.

[rfourquet]

Yes of course you are right, I somehow confused this use case with uses of seed! in Random tests.

[rfourquet]

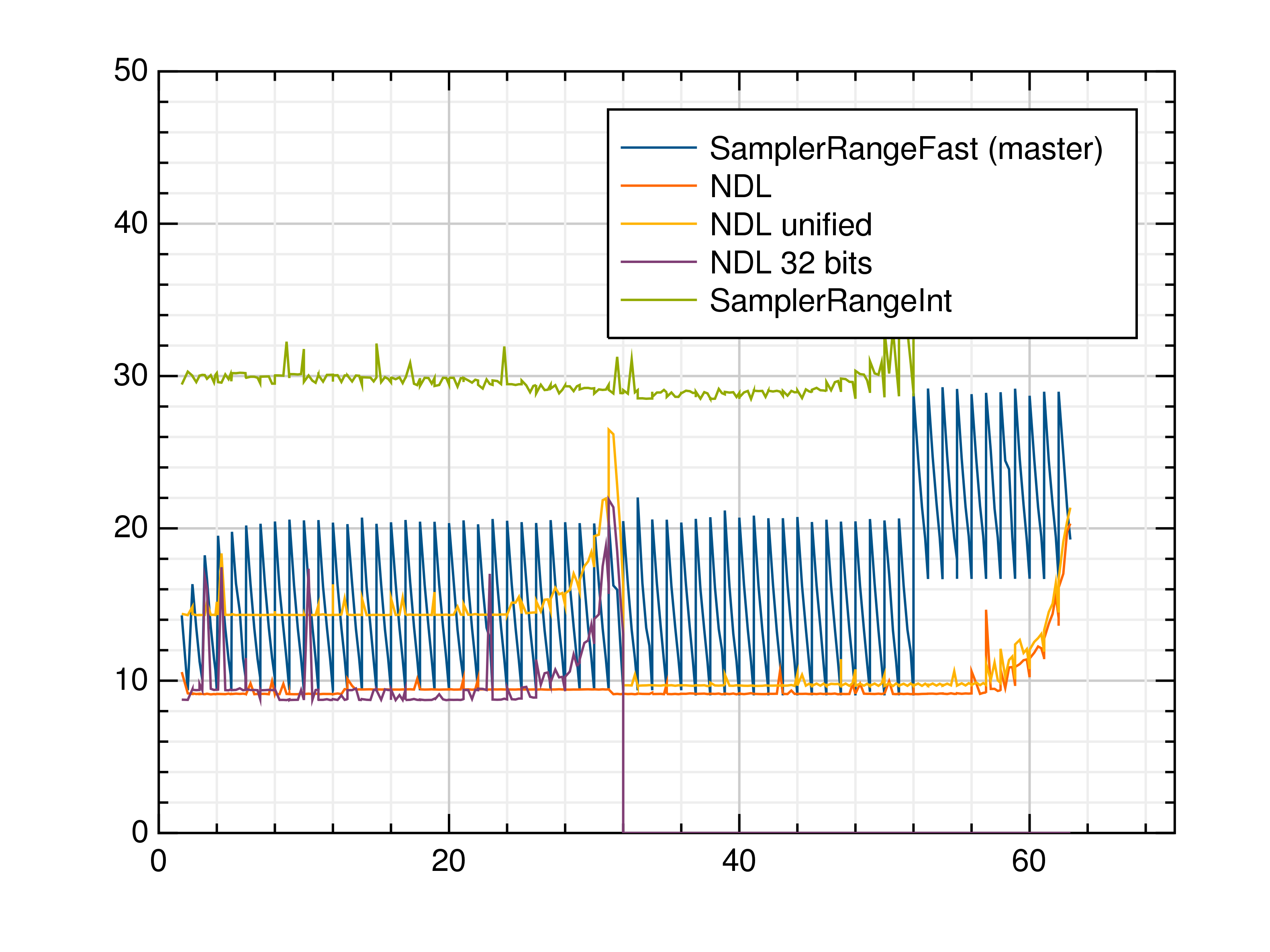
While updating to make this algorithm (NDL) the default, I realised that we have a test garanteeing that e.g. rand(1:9) will give the same result regardless of the architecture (i.e. regardless of the value of Int).

Unfortunately here this means that if we want to maintain this property, there is a (small) cost to pay. I may have made a mistake of course, but this is what I currently understand. Let's call "NDL Unified" the modification of rand in this PR that respect the garantee mentioned above, by adding this line at the beginning, to call the 32 bit version when the range length fits in 32 bits:

    if U === UInt64 && !iszero(sp.s) && sp.s <= typemax(UInt32)
        return rand(rng, SamplerRangeNDL(sp.a, sp.s % UInt32))
    end

Here are the observations (see graph below) for MersenneTwister, where input range is UnitRange{Int64} except for NDL 32 bits:

• the default for MersenneTwister is SamplerRangeFast, whose efficiency decreases for a length from 2^n to 2^(n+1)-1, and is good again at 2^(n+1). There is a pic at 2^52 because MersenneTwister generates 52 bits natively (SamplerRangeFast is somewhat optimized for that)
• NDL (32 or 64 bits depending on input) follows the best case of SamplerRangeFast, with efficiency decreasing when approaching full capacity (2^64 here)
• NDL unified: on the [1:2^32] interval, the performance is not so attractive compared to the status quo (expect it's more predictable, no "pics"), in particular when approaching "full capacity" at 2^32. I don't really understand why it becomes basically as efficient as NDL after 2^32
• NDL 32 bits, which corresponds to e.g. rand(UInt32(1):UInt32(9)): this is slightly better than NDL, and seems to reflect the difference between rand(UInt32) and rand(UInt64) involved in the computation (maybe about 1ns difference).
• Another solution, NDL64 (opposite solution to NDL unified): not plotted, but should look like NDL, where even 32 bit ranges call the 64 bit version, unconditionally. The problem is that for RNGs where rand(UInt64) can be twice as expensive as rand(UInt32), we really loose efficiency for small ranges, i.e. NDL32 (which would be more advantageous for this RNG than in this graph) would be unavailable.
• SamplerRangeInt: the default for non-MersenneTwister

(EDIT: I don't know why the x/y labels disappear when saving the graph to disk, x is "log2(range length)" and y is "time in ns".)

So, I my favorite solution is to drop the guarantee that rand(1:9) will give the result whether Int is 32 or 64 bits, as it gives access to the best performance, and it allows to specifically ask for the 32 version (by converting a range to 32 bits types) if deemed more favorable. If not acceptable, I would otherwise choose NDL64. What do you think?

[chethega]

This goes into the next release and won't be backported, right?

Then I am all for dropping the guarantees.

However,

julia> s=Random.SamplerRangeNDL(UInt128(1):UInt128(2));
julia> @btime rand($s);
  477.703 ns (11 allocations: 186 bytes)

julia> s2=UInt128(1):UInt128(2);
julia> @btime rand($s2);
  25.301 ns (0 allocations: 0 bytes)

[rfourquet]

This goes into the next release and won't be backported, right?

It would be great that it goes in the next release, but for sure won't be backported indeed!

However, [...]

Yeah, there is a widen operation involved (which gives BigInt for UInt128), so this will be enabled only for types upto 64 bits. When you define widen(::Type{UInt128}) = UInt256, then NDL seems to still be faster than the status quo.
Also, it would be interesting to see if NDL can be extended efficiently to BigInt.

[GregPlowman]

Here's what seems like a minority voice.

When developing some simulations, I like to be able to compare results with previous runs. I guess this is a sort of unit test. I might experiment with algorithmic changes, performance enhancements etc. and then re-run the sim and check whether I'm still getting the same results.

In fact, I just upgraded from Julia v0.6 through v0.7, v1.0 and v1.1, and wanted to compare the new sim results to the old v0.6 ones. But I needed to implement the same custom rand(1:n) in both v0.6 and v0.7 so that the sequence was the same in both versions.

I understand the tension between progress and being held back by guarantees, especially when it is deemed the guarantee is of little benefit &/or the progress is of significant benefit.

However, I do want to point out the difference between random sequence guarantees across Julia versions, and across architectures within the same Julia version. I run my simulations across a network cluster and check the results against previous runs. In my case, all machines are 64-bit, but this would break in mixed-architecture clusters.

I don't like that the random sequence guarantee is broken across versions, but I'm happy to sacrifice that for progress. I feel less comfortable if the guarantee is broken across architectures on the same Julia version.

[rfourquet]

I appreciate the usefulness of compatibility between architectures, however it's already not compatible for rand(Int), but more importantly it seems to me that using Julia on 32-bits architectures is really marginal. So everyone having to pay a price for something quite rare (unless my impression is mistaken) doesn't look like a good balance to me.

I would favor having a opt-in way of getting reproducibility. One of them would be to simply create the range with Int32 values, e.g. Int32(1):Int32(9). Another would be to have an RNG (e.g. a wrapper of MersenneTwister) which offers some guarantees. If this RNG was "frozen", we could even imagine being able to guarantee stream reproducibility across some Julia versions for some types/ranges.
Just my 2c.

[rfourquet]

Also, I just read Numpy's policy on RNG https://www.numpy.org/neps/nep-0019-rng-policy.html, this may be relevant to the discussion.

[chethega]

Can we put up some docs for an official reproducibility + rng-stream policy? Is there an issue/PR that discusses that?

As far as I understood, (1) we have no reproducibility between 32 bit and 64 bit anyway, (2) new releases may break RNG streams 32208, 30617, (3) we attempt to avoid breaking RNG streams on bugfix / backports.

Do we attempt reproducibility between architectures (e.g. aarch64 vs x86_64 vs power)?

Since we break RNG streams on releases, it would be almost sensible to codify this by having seeding of the RNG incorporate the version (like 1.2, 1.3, etc) and potentially word size and potentially architecture. That way, everybody knows that a new release will change all random streams, and randomized testsets will need to be regenerated. Nobody will then incorrectly rely on cross-version reproducibility of random streams.

The worst case is random streams being almost reproducible, which is what we have now (and what numpy appears to be doing).

If we codify this dependence of RNG streams, then we also lay the groundwork for replacing mersenne twister with alternatives that are faster (e.g. xoroshiro) or better (i.e. cryptographic like aes-ctr with hardware acceleration).

[rfourquet]

Can we put up some docs for an official reproducibility + rng-stream policy? Is there an issue/PR that discusses that?

The comment from which I grabbed the link I posted above was just requesting that, and there was a small discussion yesterday on slack (triage channel) on this topic too. There is no open issue AFAIK though.

I find your idea of "codifying" in each release the breaking behavior in the seeding process quite interesting!

[stevengj]

Official docs on reproducibility of random streams was merged in #33350.

[StefanKarpinski]

I have also for some time wanted to hash seed values with a cryptographic hash like SHA1 or SHA256 before passing that seed value on to the underlying RNG for actual seeding. The reason being that there are often bad seed values for RNGs and there's strong evidence that close RNG seed values produce streams that have significant correlation. By using a cryptographic hash on the seed value before passing it on to the RNG, you get (more) thoroughly uncorrelated streams for sequential seed values. It also makes it easy to use a tuple of seed values, which can be handy in situations where you want a whole family of reproducible RNG streams.

[rfourquet]

Official docs on reproducibility of random streams was merged in #33350.

This is great, but does not explicitly cover the question (which needs to be resolved here): must rand(1:9) generate the same stream of numbers on 32 and 64 bits architectures? I believe we never officially guaranteed that, but an explicit effort was made to have this behavior, so an explicit decision must be made to break it.

[rfourquet]

I have also for some time wanted to hash seed values with a cryptographic hash like SHA1 or SHA256 before passing that seed value on to the underlying RNG for actual seeding

Sounds like a great idea, if no-one beats me to it, I will try to implement a POC when I have some time.

[stevengj]

This is great, but does not explicitly cover the question (which needs to be resolved here): must rand(1:9) generate the same stream of numbers on 32 and 64 bits architectures?

I think this is a good property to have.

Suppose you have a stochastic program that is working on a 64-bit machine but failing on 32-bit, and you are trying to isolate the source of the failure. Not being able to generate the same random number stream on both architectures with the same Julia versions seems like it would make debugging a lot harder.

[rfourquet]

I think this is a good property to have.

Certainly, but in the present case it's at the cost of performance, and there is a work-around (use Int32(a):Int32(b)).
@mschauer would you share your opinion on this?

[mschauer]

I overlooked this issue. Let me come back.

[StefanKarpinski]

I think we can generally optimize for 64-bit systems at the expense of 32-bit ones. If people need really high performance, they're generally not working on 32-bit computers these days.

[rfourquet]

I think we can generally optimize for 64-bit systems at the expense of 32-bit ones

I fully agree. But even then, we have a decision to make: do we keep "stream compatibility" between 32 and 64 architectures (i.e. Random.seed!(0); rand(1:9) gives the same output whatever Int is)?

• if so, we have the choice between "NDL-unified" and "NDL64" as described above. If we favor "optimize for 64-bit systems", then we choose "NDL64", which is a pessimization for 32-bit systems.
• otherwise, each architecture gets its native algorithm ("NDL").

I would vote for the latter option.

Note that with other RNGs, 64 bits generation might be the "native output" even on 32-bits systems, in which case it's possible to have "sream compatibility" for free.

Off-Topic: since a couple of days, I was thinking to implement passing seeds to a crypto hash function, and I realize now it was not at all an original thought of mine 🙈 !