-
Notifications
You must be signed in to change notification settings - Fork 629
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
subpixel averaging for boundaries of variable-material objects #1399
base: master
Are you sure you want to change the base?
Conversation
| } | ||
|
|
||
| /* check for trivial case of only one object/material */ | ||
| if (material_type_equal(mat, mat_behind)) { | ||
| if (is_variable(mat)) eval_material_pt(mat, vec_to_vector3(v.center())); | ||
| goto trivial; |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
In #1539, this will branch to the new averaging procedure if mat is a variable material.
d0b870d
to
4c02faf
Compare
ce93958
to
bf5296c
Compare
|
|
||
| Requires moderately horrifying logic to figure things out properly, | ||
| stolen from MPB. */ | ||
| static bool get_front_object(const meep::volume &v, geom_box_tree geometry_tree, vector3 &pcenter, | ||
| const geometric_object **o_front, vector3 &shiftby_front, | ||
| material_type &mat_front, material_type &mat_behind) { | ||
| material_type &mat_front, material_type &mat_behind, | ||
| vector3 &p_front, vector3 &p_behind) { |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Note that we added p_front and p_behind here — this is so that we have a point to evaluate the material at if it is a variable materials (grid or user).
This PR implements subpixel averaging for the boundaries of objects with variable materials (e.g. user-defined material functions). I realized that we can still handle this case accurately and efficiently, as long as the material function is continuous inside the object.
For example, here is a simulation of transmitted power through a cylinder of linearly-varying ε:

If I compute and plot the convergence with respect to resolution using this code:
then before this PR I get first-order convergence due to the lack of subpixel averaging at the boundaries of the cylinder:
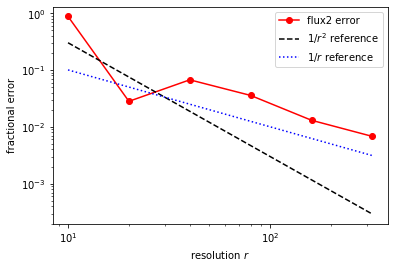
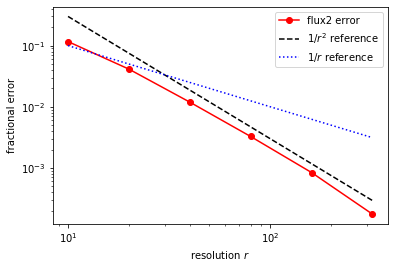
but after this PR I get second-order convergence: