Note: This repository is still developing.
- 01. Traveling Salesman Problem (TSP)
- 02. Knapsack Problem
- 03. Minimum Spanning Tree
- 04. Vehicle Routing Problem (VRP)
- 05. Shortest Path Problem
Combinatorial Optimization is a branch of optimization focused on finding an optimal solution from a finite set of discrete solutions. It is widely applied in fields like operations research, computer science, engineering, logistics, and artificial intelligence. The primary goal of combinatorial optimization is to determine the best combination or ordering of elements that satisfies specific criteria and constraints, often while minimizing or maximizing a particular objective function, like cost, time, or efficiency.
-
Discrete and Finite Solutions: Solutions in combinatorial optimization are drawn from a discrete, finite set of possible options, as opposed to continuous optimization, where solutions can be any value within a range.
-
Complexity and NP-hardness: Many combinatorial optimization problems belong to the class of NP-hard problems, meaning they are computationally intensive, and no polynomial-time algorithms are known to exist for finding optimal solutions to large instances of these problems.
-
Objective Function and Constraints: Each problem has an objective function (e.g., minimize cost, maximize profit) and may have constraints (e.g., capacity limits in Knapsack, connectivity in TSP) that must be met by feasible solutions.
-
Traveling Salesman Problem (TSP): Find the shortest possible route that visits each city exactly once and returns to the origin city.
-
Knapsack Problem: Maximize the total value of items packed into a knapsack without exceeding its weight limit.
-
Graph Coloring: Color the vertices of a graph such that no two adjacent vertices share the same color while minimizing the total number of colors used.
-
Bin Packing: Pack objects of different sizes into a finite number of bins in a way that minimizes the number of bins used.
-
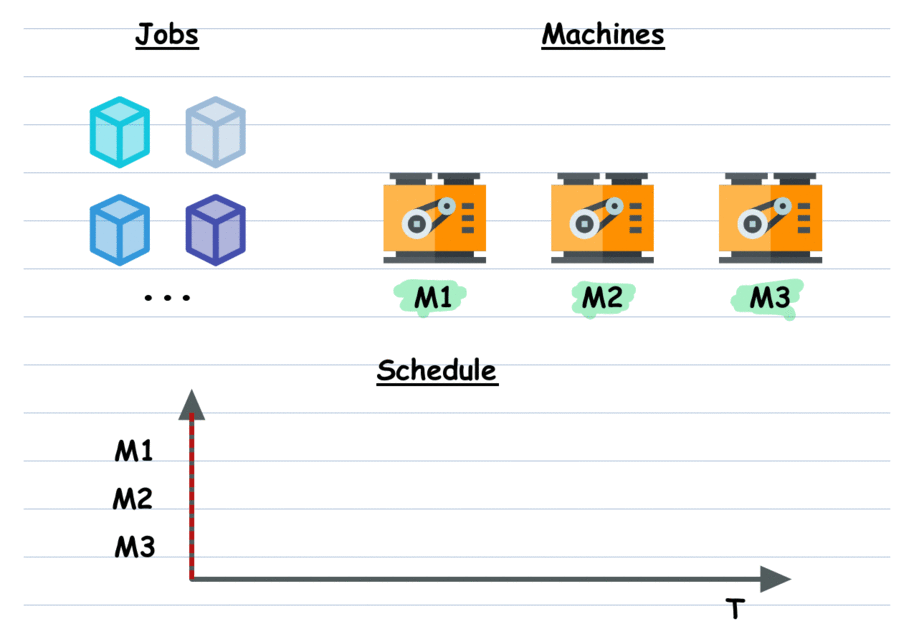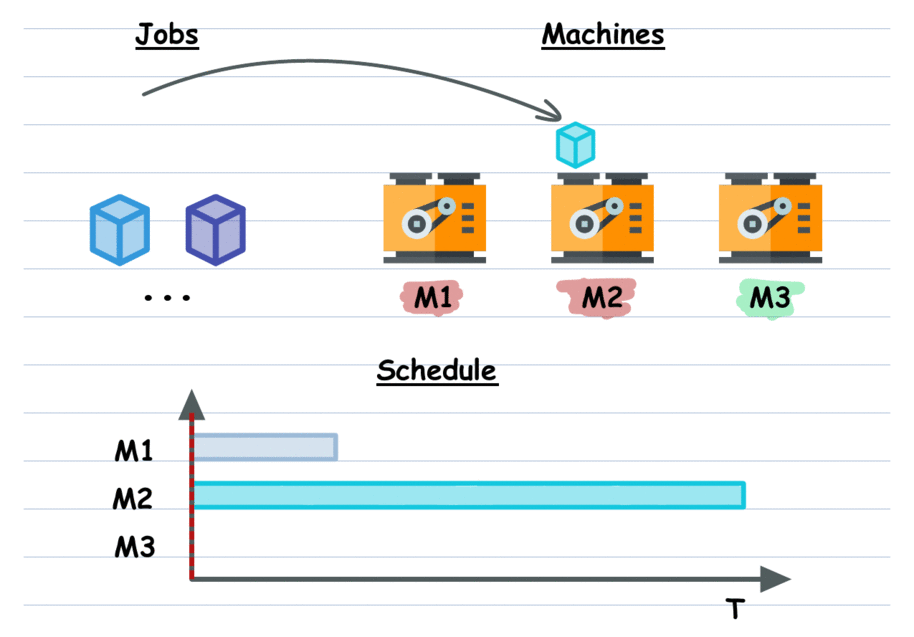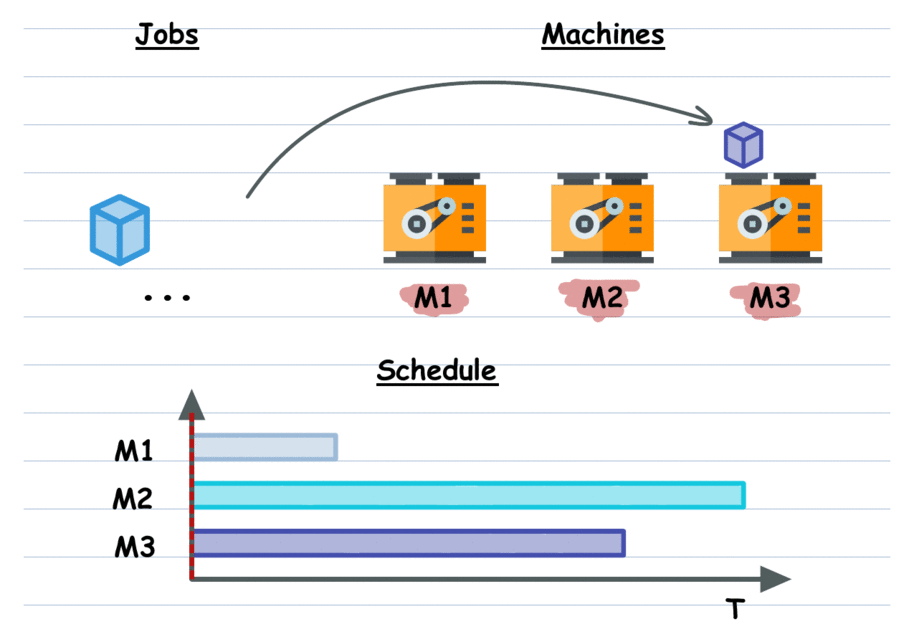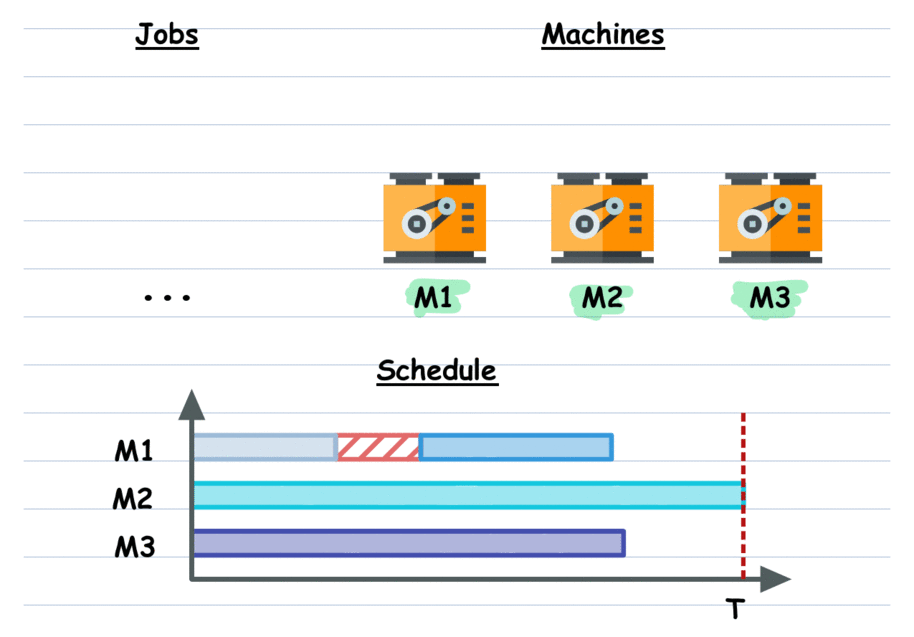
Job Scheduling: Schedule tasks on resources (machines or workers) to minimize total completion time or other objectives.
-
Assignment Problem: Assign tasks to agents in a way that minimizes the total cost or maximizes overall efficiency.
-
Exact Methods: Aim to find the optimal solution. Common exact methods include:
- Dynamic Programming: Breaks the problem into overlapping subproblems, solving each subproblem once and reusing results (e.g., for TSP and Knapsack).
- Branch and Bound: Systematically explores solution branches and prunes suboptimal branches based on bounds to find the optimal solution.
- Integer Linear Programming (ILP): Uses linear programming with integer constraints, commonly solved by solvers like CPLEX or Gurobi.
-
Heuristic Methods: Provides good, feasible solutions in a reasonable time but doesn’t guarantee optimality.
- Nearest Neighbor (for TSP): Constructs a tour by repeatedly visiting the nearest unvisited city.
- Greedy Approaches (e.g., for Knapsack and Bin Packing): Make locally optimal choices at each step to build a solution.
-
Metaheuristic Methods: Higher-level procedures that guide simpler heuristics to explore the solution space effectively. Metaheuristics are particularly useful for large, complex problems.
- Simulated Annealing: Mimics the annealing process in metallurgy, allowing for probabilistic "uphill" moves to escape local optima.
- Genetic Algorithms: Uses evolutionary principles to evolve solutions over generations.
- Ant Colony Optimization: Inspired by the behavior of ants finding paths, using pheromone trails to probabilistically choose paths.
- Tabu Search: Uses memory structures to avoid cycling back to recently visited solutions.
Combinatorial optimization is applied in diverse real-world scenarios, such as:
- Logistics and Supply Chain: Route planning (e.g., for delivery trucks), warehouse space optimization, and resource allocation.
- Telecommunications: Network design and resource allocation in data networks.
- Manufacturing: Job scheduling, assembly line balancing, and quality control.
- Finance: Portfolio optimization, risk management, and asset allocation.
- AI and Machine Learning: Hyperparameter tuning, feature selection, and neural architecture search.
- Scalability: Exact algorithms can become impractical for large problem instances due to their exponential time complexity.
- Quality of Solution: Heuristic and metaheuristic methods may not guarantee optimal solutions, so trade-offs between solution quality and computational effort are often necessary.
- Constraint Handling: Complex real-world applications often involve intricate constraints, making modeling and solution finding even more challenging.
Combinatorial optimization is about making the best choice out of a discrete set of possible solutions under given constraints. It encompasses a variety of problems with significant implications across numerous fields. The choice of solution approach—exact, heuristic, or metaheuristic—depends on the problem size, required solution quality, and available computational resources. The field continues to evolve, integrating advanced computational techniques to address increasingly complex real-world applications.