Breadth-first Tree Traversal

Why is this important?

This workshop is important because:

Trees are very common in real-world applications. Examples include the DOM tree, which structures elements on a web page, and b-trees, which are used to index databases like PostgreSQL.

When we're storing data in trees, it's important to be comfortable using methods to move through that data. A really common problem is searching for a particular node or set of nodes within a tree. "Traversing" a tree just means moving through all of its nodes, and it's a common strategy to search trees!

What are the objectives?

After this workshop, developers will be able to:

• Describe and draw breadth-first tree traversal.
• Pseudocode breadth-first search.
• Identify use cases for breadth-first search.

Where should we be now?

Before this workshop, developers should already be able to:

• Explain tree terms: root, node, edge/branch, leaf, parent, child.
• Compare and contrast graphs, trees, binary trees, and binary search trees.
• Describe and draw a queue data structure.

Breadth-first Search

Breadth-first search is one algorithm for searching through graphs, looking for one or more nodes that meet some search criteria.

In a binary search tree, we can find nodes based on keys quite quickly if we take advantage of the fact that each node's left subtree contains smaller keys and each node's right subtree contains larger keys.

Breadth-first search is more general -- it doesn't make any assumptions about the relationships among nodes' keys. In fact, we can search by criteria that aren't based on keys at all. With a tree of hex color names, we could use Breadth-first Search to find all of the colors created by one user.

Breadth-first search chooses a start node and "visits" every node of a graph in order of how far the node is from that start. In a tree, we pick the root as the start, and distance is just the number of edges from the root to the node.

Breadth-first Search spreads like a mold across the tree or graph, moving outward one step at a time from its start location.

Breadth-first Traversal

Here's a rundown of breadth-first tree traversal:

1. Set up a queue to track which nodes to visit.

2. Add the root to the queue.

3. Until the queue is empty, process the first node in the queue with the following steps:

   • remove the node from the front of the queue
   • add the node's children to the back of the queue
   • do whatever additional processing you'd like!

Check for Understanding

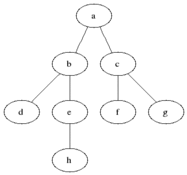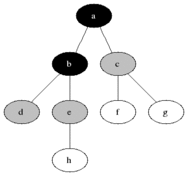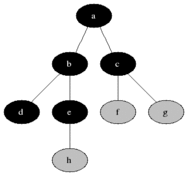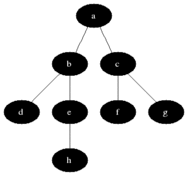
1. Draw the queue at each step in breadth-first traversal for the tree below:

click for answer

  [D]
  [B, F]      (dequeue D, enqueue its children)
  [F, A, C]   (dequeue B, enqueue its children)
  [A, C, E]   (dequeue F, enqueue its children)
  [C, E]      (dequeue A, enqueue its children)
  [E]         (dequeue C, enqueue its children)
  []          (dequeue E, enqueue its children)

Or, you could add the children starting at the "right" each time:

  [D]
  [F, B]      (dequeue D, enqueue its children)
  [B, E]      (dequeue F, enqueue its children)
  [E, C, A]   (dequeue B, enqueue its children)
  [C, A]      (dequeue E, enqueue its children)
  [A]         (dequeue C, enqueue its children)
  []          (dequeue A, enqueue its children)

What is the Big-O runtime complexity of breadth-first traversal?

Exercises: Breadth-first Tree Search

1. In English, describe how you would use breadth-first search to find any node with a given key. Your algorithm should assume you have a tree data structure and that you can access each node's key its array of children. (Do not assume it's a binary search tree.) You should also assume you're given a target key to match.

2. On the whiteboard, pseudocode a breadth-first search function. Assume you have a tree data structure that allows the following operations:

   • given a tree/node my_tree, get the root of the tree with my_tree
   • given a tree/node, get the key of the node with .key
   • given a tree/node, get the children of the node with .children

3. Copy the starter code in either tree.js or tree.rb. Code up your breadth-first search function in one of these files. There are informal "tests" at the bottom of each file that show what the output should be. Run node tree.js or ruby tree.rb to see these tests work on your file.

4. How would you modify your breadth-first search function to work on a binary search tree?

5. How could you use breadth-first search to check whether a binary search tree is balanced?

Binary search trees can be faster than arrays at keeping data sorted when you insert and remove nodes, but only if the binary search tree is balanced, because a balanced tree has the minimum possible number of levels to store all its nodes.

We can check that a tree is balanced by looking at where it has "missing children," room where nodes could have a child but don't. A tree is balanced if all of the missing children are at the very bottom level of the tree or just one level higher.

1. How could you modify breadth-first search to pick out a group of nodes? What if you're selecting nodes based on some other characteristic instead of just the key?

2. You run a website where users can assign creative names to colors. You store named colors as nodes in a self-balancing binary search tree, where the key of a node is the hex code of its color (for example: #30af99, #c0ffee). For a user's profile page, you'd like to show all the colors created by that user. How could you modify the binary search tree and a breadth-first search algorithm to find all the colors created by a particular user?