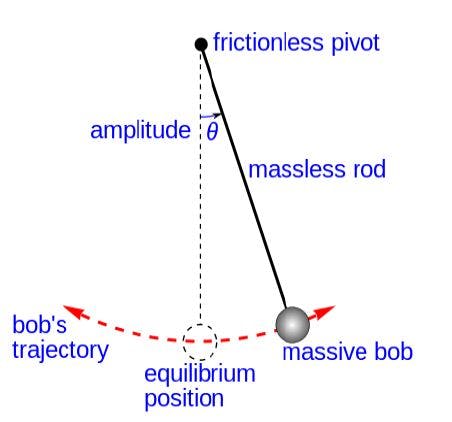
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subjected to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing.
The simple gravity pendulum is an idealized mathematical model of a pendulum. This is a weight (or bob) on the end of a massless cord suspended from a pivot, without friction. When given an initial push, it will swing back and forth at a constant amplitude. Real pendulums are subject to friction and air drag, so the amplitude of their swings declines.
The period of swing of a simple gravity pendulum depends on its length, the local strength of gravity, and to a small extent on the maximum angle that the pendulum swings away from
vertical, θ0, called the amplitude. It is independent of the mass of the bob. If the amplitude is limited to small swings, the period T of a simple pendulum, the time taken for a complete cycle, is
Where L is the length of the pendulum and g is the local acceleration of gravity.
For small swings the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude. This property, called isochronism, is the reason pendulums are so useful for timekeeping. Successive swings of the pendulum, even if changing in amplitude, take the same amount of time.
For larger amplitudes, the period increases gradually with amplitude so it is longer than given by equation (1). For example, at an amplitude of θ0 = 23° it is 1% larger than given by (1). The period increases asymptotically (to infinity) as θ approaches 180°, because the value θ0 = 180° is an unstable equilibrium point for the pendulum. The true period of an ideal simple gravity pendulum can be written in several different forms, one example being the infinite series:
The local value of acceleration due to gravity can be calculated as
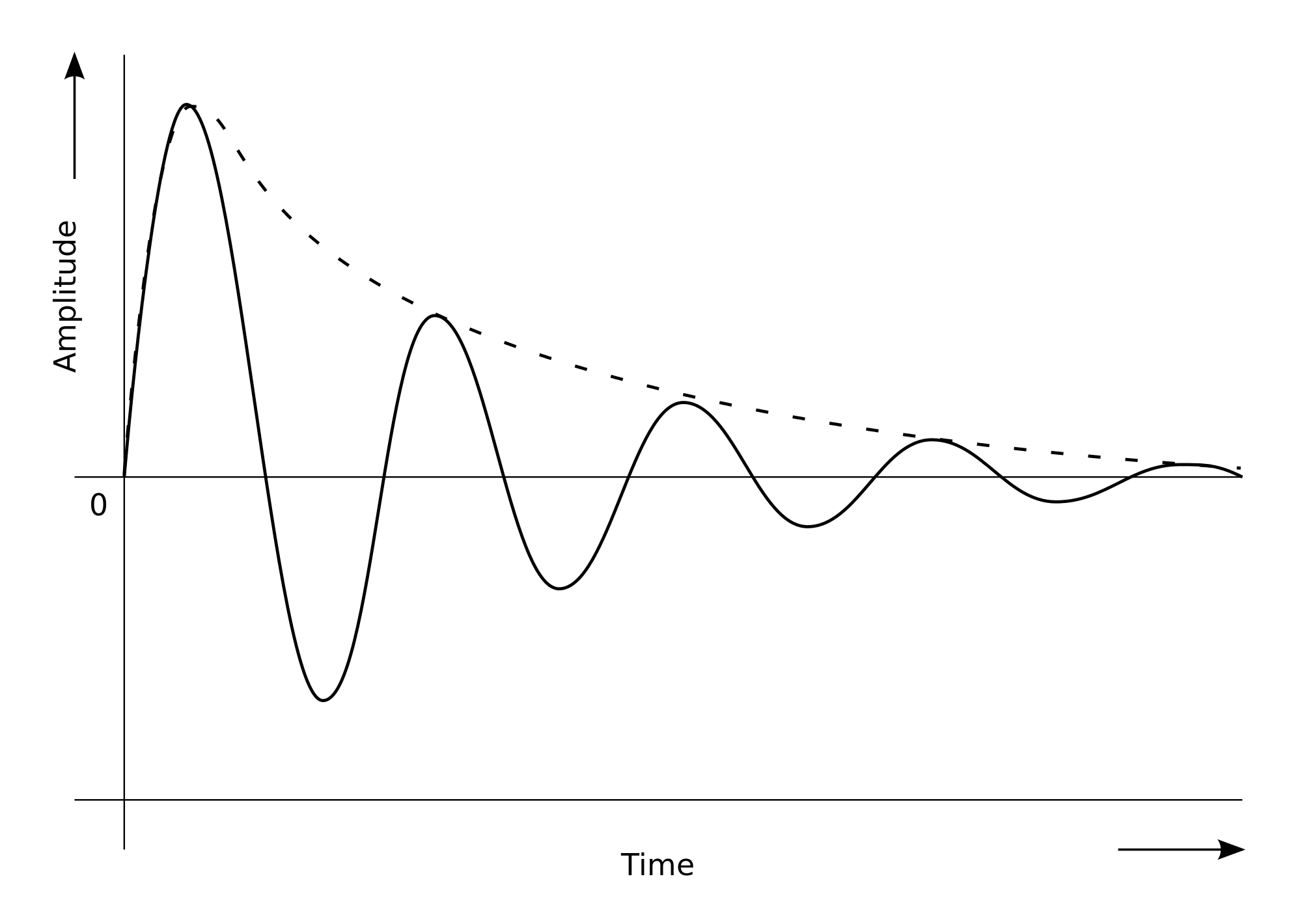
Damping is an influence within or upon an oscillatory system that has the effect of reducing, restricting or preventing its oscillations. In most physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Due to damping the amplitude of oscillation goes on decreasing and finally reaches mean.
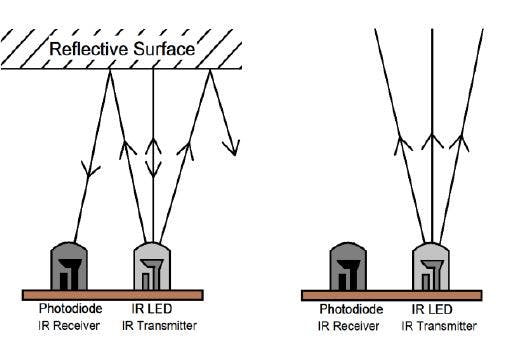
The principle of an IR sensor working as an Object Detection Sensor can be explained using the following figure. An IR sensor consists of an IR LED and an IR Photodiode; together they are called as Photo – Coupler or Opto – Coupler.
When the IR transmitter emits radiation, it reaches the object and some of the radiation reflects back to the IR receiver. Based on the intensity of the reception by the IR receiver, the output of the sensor is defined.
The Arduino UNO is an open-source microcontroller board based on the Microchip ATmega328P microcontroller and developed by Arduino. The board is equipped with sets of digital and analog input /output (I/O) pins that may be interfaced to various expansion boards (shields) and other circuits. The board has 14 Digital pins, 6 Analog pins, and programmable with the Arduino IDE (Integrated Development Environment) via a type B USB cable. It can be powered by a USB cable or by an external 9 volt battery, though it accepts voltages between 7 and 20 volts. The ATmega328 on the Arduino Uno comes preprogrammed with a boot loader that allows uploading new code to it without the use of an external hardware programmer. It communicates using the original STK500 protocol.
Arduino Uno uses C/C++ compiler to compile the uploaded code and performs its function. In this project we use Arduino to measure the time period of an oscillation and thus calculates the local value of acceleration due to gravity.
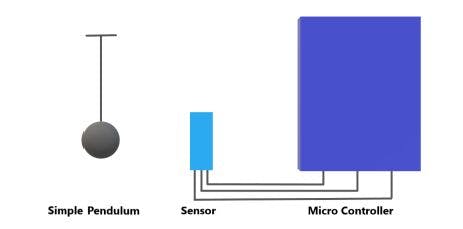
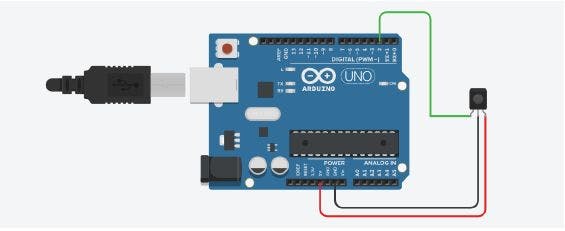
The whole experiment setup consists of a simple pendulum, a virtual clock using IR proximity sensor and microcontroller. The schematic diagram of experimental setup is shown.
The proximity sensor can be connected to Arduino Uno as
A good and strong frame is constructed using wood or other suitable material to hold the pendulum firm, which reduces shake and thus reduces errors.
A simple pendulum of suitable length (~15 cm) is made using a bob and a massless inextensible string.
Place the IR sensor at the suitable distance below or beside the bob of simple pendulum so as to get the maximum accuracy in measurement. The accuracy is verified for various baud rates of microcontroller.
And this is how the sensor works, in an oscillation whenever the bob covers the IR sensor it will return a value 0 to the microcontroller otherwise it will return 1 to the microcontroller.
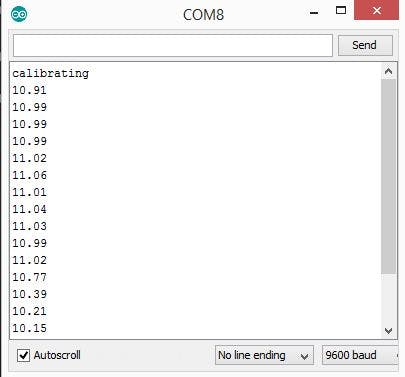
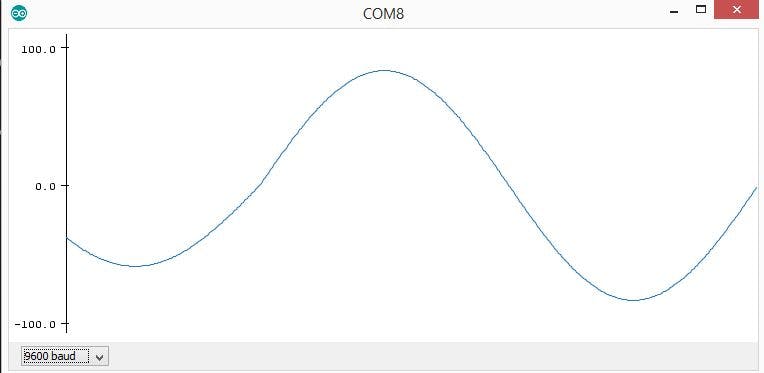
Arduino Uno is the brain of this project, it reads the value from the IR proximity sensor and the measure the time between two consecutive 0 values, is the half of time period. For each half oscillation it calculates the value of ‘g’ and by adding the consecutive ‘g’ values of two half oscillations the mean value of ‘g’ for one oscillation is found. As the oscillations proceed the amplitude of oscillations goes on decreasing. By the data collected using IR sensor a real time damping curve is drawn.
Arduino uses C/C++ code with its own slight modifications. Code has two parts, the major part is to analyze sensor and all determines whether the bob is in the mean position or not. digitalRead() function is used to read the sensor data. If the value is 0 the bob is in the mean position and if 1 it is not. The micros()function is used to measure the time period.
Using the Serial.println()function the value of ‘g’ is printed and a real time damping curve is drawn in the serial plotter.
For small amplitude oscillations the local value of acceleration due to gravity is printed in the serial monitor.
Also a real time damping curve is observed in the serial plotter
Calculating on paper is never an easy job. When it comes to complex formulas it is nothing but a short nightmare. So it is better to replace the scary calculations with a small computer program. The better part is that the observations and values are more accurate when using sensors. In this project we have automated the tedious calculations with a small computer program. In this technical era it seems to be worth.