-
Notifications
You must be signed in to change notification settings - Fork 19
Distribution Functions
An uncertain element in your model may take on a range of possible values: some more likely, some less likely. To define uncertain variables in Argo, choose a probability distribution function from the wide selection of Argo distribution functions. Although cells in the spreadsheet containing distribution functions display a single number, the cell represents a sample of possible values that the simulation will produce. The available distributions in Argo can take on many shapes to represent the real-world system being modeled.
Table of Contents
- Distribution Functions
You can define an Argo distribution in several ways. First, you can type the function directly into the cell. This method offers no description of the distribution, so use it only if you are familiar with the order of the parameters. Second, you can use the Excel Function Wizard, where the distributions are described and the parameters are listed by name. Third, you can select Distribution from the Argo tab, which shortcuts to the appropriate menu in the Excel Function Wizard method. Below are more detailed instructions for each of these three methods.
-
Entering distributions directly into cells
- With the Argo add-in installed, select a cell in the workbook.
- Enter
=rtainto the cell to bring up Excel's IntelliSense list, which will contain the complete library of Argo distributions and results - Select the appropriate distribution from the list
- Enter appropriate parameters for the distribution
- Press Enter to assign the distribution
-
Entering distributions into cells using the Excel Function Wizard
- On Excel's ribbon, select the Formulas tab and the Insert Function button (on the far left)
- On the select a category dropdown menu, select RTA Discrete Distributions or RTA Continuous Distributions
- Select the desired distribution and enter the appropriate distribution parameters
- Select OK to assign the distribution
-
Entering distributions into cells using the Argo tab
- On the Argo tab, click Distribution and select the desired distribution
- Enter the appropriate distribution parameters into Excel's Function Wizard
- Select OK on Excel's function wizard to assign the distribution
Please, note that every distribution has to be defined in its own cell, so that a cell containing a distribution should not contain anything else in it. For instance, in the figure below we have cell D2 defined as rtaNormal(0,1) and cell E2 defined as rtaUniform(0,5).
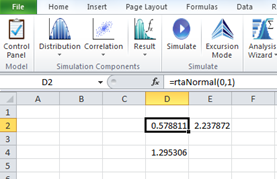

The correct way to multiply two distributions together is to do so in a separate cell, shown below in cell D4 defined to be =D2*E2.

It is incorrect to do any other operations in the same cell where a distribution is defined. Below shows an incorrect way to combine distributions in Argo.

Each RealTime Analytics distribution function has its own purposes and its own parameters. There are also optional parameters common to all distributions, which the user may list after the distribution-specific parameters: Val Functions. Within the formula for each distribution, after the mandatory parameters are inputted, these functions can increase the functionality of a distribution. Below, each val function is described in detail.
valLIKELIHOOD
This function defines the probability of occurrence for a distribution. The probability is a number between 0 and 1 (inclusive), with the default being 1. When this function is added to the parameters, the simulation will either generate a number based on the distribution and other parameters, or (if the probability is less than 1) the simulation may generate a 0 to denote that the event did not occur. Therefore, if the probability of occurrence is set to 0, the simulation will only generate 0 for each simulated trial. If it is .5 (50% probability of occurrence), around half of the trials will be 0 and the other half will be values based on the distribution.
Example: =rtaBeta(2,5,0,1,valLikelihood(.75))
valLOWERBOUND
This function defines the lower truncation threshold for a distribution. In other words, a distribution will not simulate a value below the set lower bound. The lower bound can be any value in a distribution's domain (accepted values). For instance, the log-normal distribution accepts values greater than or equal to 0, thus including any value less than 0 for valLowerBound for the log-normal distribution will give the #VALUE! Error.
Example: =rtaNormal(0,1,valLowerBound(-2))
Example: =rtaNormal(0,1,valLowerBound(-2),valUpperBound(2))
valNAME
This function names a distribution or result so that it can more easily be organized and found within the control panel. Any combination of words, spaces, numbers, or symbols can be used to create the name. All you need to do is type =valNAME(“ Blank “). Don't forget the quotation marks!
Example: =rtaLognormal(10,1,valName(“Risk1”))
Example: =rtaResult(SUM(A1:A5),valName(“Total Cost”))
valPOINTESTIMATE
This function specifies what value is shown within excel. Because distributions are built of a large sample of data and change dynamically in Argo, it is very difficult to keep a neat and uniform worksheet in the model. Point estimate solves this problem by placing a single value to represent the cell value at all times. The below example will show 0.7 in the cell instead of showing a trial from the simulation.
Example: =rtaExponential(0.7,valPointEstimate(0.7))
valSHIFT
This function defines a shift parameter that can shift all of the distribution samples. This allows you to maintain the same distribution while shifting output to the appropriate one for the respective model. The example below will have a distribution with a mean of 100.
Example: =rtaNormal(0,1,valShift(100))
valUPPERBOUND
This function defines the upper truncation threshold for a distribution. In other words, a distribution will not simulate a value above the set upper bound. The upper bound can be any value and can be applied in a number of facets including cost and sale price forecasting.
Example: =rtaNormal(0,1,valUpperBound(2))
Example: =rtaNormal(0,1,valLowerBound(-2),valUpperBound(2))
Similar to the valPOINTESTIMATE function, you can have each distribution in the workbook to display a point estimate at all times. The default setting will display a random trial each time the worksheet is recalculated.
On the Argo ribbon, select Options and select the Cell Preferences tab as shown below.

Under the section labeled "Distribution Return Values" select the drop down menu to select which value you want to be returned.
You can select to have the a Random Sample trial to be displayed (this is the default), mean, median, or mode.
Note: the valPOINTESTIMATE will take precedence over the Distribution Return Values setting, i.e. if you set the Value Returned to Mode and a distribution set to =rtaNormal(0,1,valPOINTESTIMATE(1)) the cell will return a 1 rather than the mode, which in this distribution would be 0.
All probability distributions can be classified as discrete probability distributions or as continuous probability distributions, depending on whether they define probabilities associated with discrete variables or continuous variables.
This section focuses on continuous probability distributions. A continuous probability distribution can take on any value in a specified range.
This function defines a beta distribution in the selected cell. The beta distribution is a family of continuous probability distributions defined on the interval (Min, Max). Two positive parameters, Alpha and Beta, determine a beta distribution's shape. The beta distribution is often used to describe the distribution of an unknown probability parameter. For example, a beta distribution may be used to guess at the probability of success that is an input for a binomial distribution or Bernoulli distribution.
Parameters:
- Alpha is one of the shape parameters. When Alpha > Beta, the distribution is left-skewed.
- Beta is the other shape parameter. When Beta > Alpha, the distribution is right-skewed.
- Min is the left endpoint of the interval where values can land
- Max is the right endpoint of the interval where values can land
When Alpha and Beta are both greater than 1, the distribution is concentrated in the middle of the interval, and the distribution resembles most natural situations.

This function defines a betaPERT distribution in the selected cell. BetaPERT is a family of continuous probability distribution that takes the same inputs as a triangular distribution, yet it outputs a beta distribution, which is smoother than the triangular distribution and occurs naturally.
Parameters:
- Min is the lowest possible value
- Mode is the most likely value, where the peak of the distribution will fall
- Max is the highest possible value

This function defines an exponential distribution in the selected cell. The exponential distribution is a continuous distribution with a strict lower limit at 0. The probability of a value near 0 is high, but the distribution decays as values increase, so that the probability that a value falls in a higher range is near 0. A faster decay Rate means a higher probability of a value near 0 and a lower probability of a high value.
Parameters:
- Rate is the speed at which the probability decays. It must be positive.

This function defines a gamma distribution in the selected cell. The gamma distribution is a continuous probability distribution with a strict lower bound, typically at 0. Its applications include modeling wait times. It is defined in terms of the gamma function with a Shape parameter k and a Scale parameter ?:

Parameters:
- Shape is a positive parameter that, when lower, yields a more left-skew distribution
- Scale is a positive parameter that, when higher, yields a more dispersed distribution

This function defines a logistic distribution in the selected cell. The logistic distribution is a symmetrical, continuous probability distribution whose cumulative distribution function is a logistic growth function.
Parameters:
- Mean is the weighted average or “expected” value. In this case it coincides with the median and the mode
- Scale is a parameter proportional to the standard deviation

This function defines a log-normal distribution in the selected cell. The log-normal distribution is a continuous probability distribution with a strict lower bound. It produces a random variable whose logarithm is normally distributed.
Parameters:
- LN Mean is the weighted average or “expected” value within the log-normal distribution
- LN Standard Deviation measures the spread of the distribution and the likely dispersion of values within the log-normal distribution

This function defines a normal distribution in the selected cell. A normal distribution is a symmetrical, continuous probability distribution that is often used as a first approximation to describe random variables that tend to cluster around a single mean value.
Parameters:
- Mean is the weighted average or “expected” value. In this case it coincides with the median and the mode
- Standard Deviation measures the spread of the distribution and the likely dispersion

This function defines a Pareto distribution in the selected cell. The Pareto distribution is a continuous probability distribution with a strict lower limit. It is sometimes used to model the distribution of incomes and other financial factors. The Pareto distribution is defined with a scale or Scale parameter xm and a Shape parameter a as follows

Parameters:
- Scale is the positive real minimum value
- Shape is a positive real parameter that, when higher, yields faster decay and a left-skewed concentration of probability toward the minimum value

This function defines a Student's t-distribution in the selected cell. The Student's t-distribution is a symmetrical, continuous probability distribution. Its shape is similar to that of the normal distribution, but Student's t-distribution has heavier tails. It arises in a variety of statistical estimation problems with the goal to estimate an unknown parameter, such as a mean value, when observed data has additive errors and the population standard deviation of these errors is unknown.
Parameters:
- Degree of Freedom is a number one less than the number of independent sample measurements: given n independent measurements, there are n-1 degrees of freedom. As degree of freedom grows, the Student's t-distribution approaches the normal distribution with mean 0 and variance 1.

This function defines a triangular distribution in the selected cell. The triangular distribution is a continuous probability distribution with lower limit Min, upper limit Max, and Mode.
Parameters:
- Min is the smallest possible value the variable could take
- Mode is the most likely value for the variable
- Max is the largest possible value the variable could take

This function defines a Trigen distribution in the selected cell. Trigen deals with a three-point estimate where the Min and the Max do not correspond to the smallest and largest possible values, but instead signify a confidence level. Trigen adjusts the estimate to produce a broader triangular distribution that exceeds the original (Min, Max) interval.
Parameters:
- Min is the estimated low value. The actual distribution will go lower
- Mode is the estimated most likely value
- Max is the estimated high value. The actual distribution will go higher
- Uncertainty Captured by the original three-point estimate is the portion (between 0 and 1) that fall inside the (Min, Max) interval
This function defines a uniform distribution in the selected cell. The uniform distribution is a continuous probability distribution where any value between the Min and the Max has an equal probability of occurring.
Parameters:
- Min is the lower limit value
- Max is the upper limit value

This function defines a Weibull distribution in the selected cell. The Weibull distribution is a continuous distribution with a strict lower bound, useful in reliability studies and quality control.
Parameters:
- Shape is a positive number that alters the shape of the distribution
- Scale is a positive number that stretches the distribution outward

All probability distributions can be classified as discrete probability distributions or as continuous probability distributions, depending on whether they define probabilities associated with discrete variables or continuous variables.
This section focuses on discrete probability distributions. A discrete probability distribution represents a countable number of values.
This function defines a _Bernoulli distributio_n in the selected cell. The Bernoulli distribution (sometimes called the “Yes-No” distribution) is a discrete, all-or-nothing probability distribution. With probability Probability, it takes on a value, Impact. With probability 1 - Probability, it takes on the value 0.
Parameters:
- Impact is numeric value of the impact of the Bernoulli distribution
- Probability, between 0 and 1, denotes the probability that the impact will occur

This function defines a binomial distribution in the selected cell. The binomial distribution is a discrete probability distribution representing the likely number of successes among a number of independent yes-no trials. Each trial has the same Probability of success. Compare with hypergeometric distribution.
Parameters:
- Trials gives the number of independent trials
- Probability is the likelihood (between 0 and 1) that any given trial succeeds

This function defines a geometric distribution in the selected cell. The geometric distribution is a discrete probability distribution concerned with the number of failed trials that precede a successful one. If each trial is independent with the same probability of success, and trials continue until one succeeds, then the geometric distribution predicts how many failures come first.
Parameters:
- Probability is the likelihood of success on each trial.

This function defines a hypergeometric distribution in the selected cell. The hypergeometric distribution is a discrete probability distribution representing the likely number of successes when trials are conducted without replacement on population whose members can be classified into two categories. The hypergeometric distribution differs from the binomial distribution because the tested members are distinct: they are drawn without replacement.
Parameters:
- Successes is the number of potential successes in the Population. If one of these members is tried, the result will be a success.
- Trials is the number of members drawn and tested.
- Population is the total number of members from which the sample is drawn.

This function defines a negative binomial distribution in the selected cell. The negative binomial distribution is a discrete distribution that measures the expected number of failures before a certain number of successes are achieved, in a situation where each independent trial has the same probability of success.
Parameters:
- Successes is the number that, until that many successes are achieved, we count the failures
- Probability is the likelihood of success on any of the independent trials.

This function defines a Poisson distribution in the selected cell. The Poisson distribution is a discrete probability distribution with a strict lower bound at 0. In some situations, events occur at a regular average rate, yet independent of the last event. The Poisson distribution represents the number of these events that will occur in a fixed time interval.
Parameters:
- Rate is the expected number of events in the interval, based on the known average rate. It is also the mean of the distribution.

This function defines a uniform discrete distribution in the selected cell. The uniform discrete distribution is a probability distribution that returns each of the integers in its range with equal likelihood.
Parameters:
- Min is a limit that no value can fall below
- Max is a limit that no value can fall above

