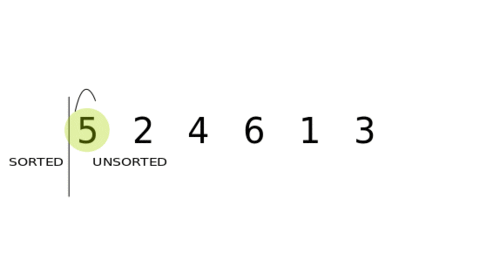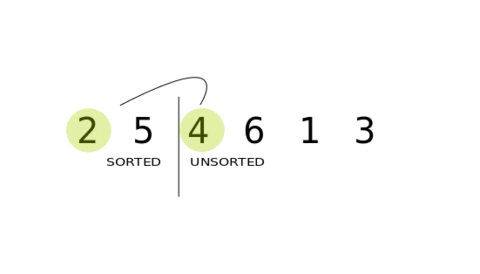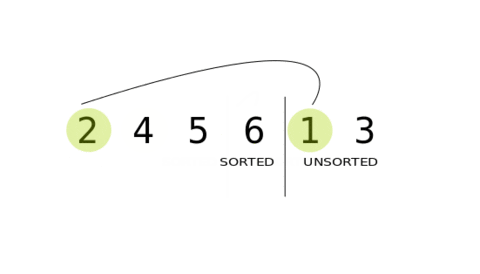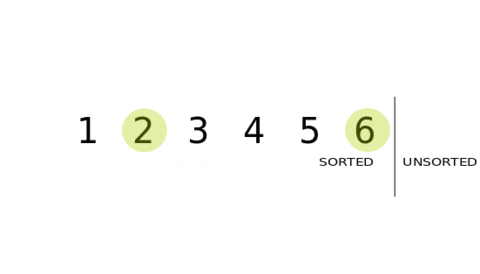Repository to store important sorting algorithms learned by Matheus Costa during his graduation. You can check the explanation of each algorithm above. Also we have here a compare file that does an empirical analysis, comparing time of the sort algorithms. There are include C++ sort() and stable_sort() on this file. Sort Algorithms are included:
- Bubble Sort
- Selection Sort
- Insertion Sort
- Binary Insertion Sort
- Merge Sort
Worst and Average Case Time Complexity: O(n*n). Worst case occurs when array is reverse sorted.
Best Case Time Complexity: O(n). Best case occurs when array is already sorted.
Auxiliary Space: O(1)
Boundary Cases: Bubble sort takes minimum time (Order of n) when elements are already sorted.
Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm.
The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from unsorted part and putting it at the beginning. The algorithm maintains two subarrays in a given array.
- 1: The subarray which is already sorted.
- 2: Remaining subarray which is unsorted.
In every iteration of selection sort, the minimum element (considering ascending order) from the unsorted subarray is picked and moved to the sorted subarray.
Its good to use for arrays that´s not too big, and for easy implementation steps require. Time Complexity: O(2*n) as there are two nested loops. And this time is the same to worst and best case, because in Selection Sort, it will go through the array n*2 time in every interaction.Auxiliary Space: O(1)
The good thing about selection sort is it never makes more than O(n) swaps and can be useful when memory write is a costly operation.
Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
AlgorithmTo sort an array of size n in ascending order:
- 1: Iterate from arr[1] to arr[n] over the array.
- 2: Compare the current element (key) to its predecessor.
- 3: If the key element is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.
- Worst Case: O(2*n) and occurs when the array is in reverse order
- Best Case: O(n) when the array is already sorted, because it will not be necessary to swap any elements, just, verify the array
We can use binary search to reduce the number of comparisons in normal insertion sort. Binary Insertion Sort uses binary search to find the proper location to insert the selected item at each iteration. In normal insertion sort, it takes O(n) comparisons (at nth iteration) in the worst case. We can reduce it to O(log n) by using binary search.
Time Complexity: The algorithm as a whole still has a running worst-case running time of O(n2) because of the series of swaps required for each insertion.
- Average and Best Case: O(log n), because we are using binary search to verify the array.
- Worst Case: O(n^2) when the array is in reverse order
Merge sort is based on Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is a key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See the following implementation for details.
Merge Sort a subarray [a...b] as follows:
Steps:- 1. If a = b, do not do anything, because the subarray is already sorted
- 2.Calculate the position of the middle element: k = ⌊(a+b)/2⌋
- 3.Recursively sort the subarray array[a...k]
- 4.Recursively sort the subarray array[k+1...b]
- 5.Merge the sorted subarray array[a...k] and array[k+1...b] into the sorted subarray array[a...b]
Merge sort is an efficient algorithm, because it halves the size of the subarray at each step. The recursion consists of O(log n) level and processing each level takes O(n) time.
Time Complexity Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation. T(n) = 2T(n/2) + θ(n), briefly we are saying that is works on O(n*log n).
- Best, Average, and Worst case: All of three works in O(n*log n), as merge sort always divides the array in two halves and takes linear time to merge two halves.
Merge Sort is useful for sorting linked lists in O(nLogn) time.In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore, the merge operation of merge sort can be implemented without extra space for linked lists.