clust4j

A Java-based set of classification clustering algorithms. Built under JDK 1.7 and tested up to JDK 1.8. This project is currently in ongoing development for the time being and should not be used in production environments

---

Installation:

clust4j 1.1.6 prerelease is now available under releases. To build the bleeding edge, use the included gradle wrapper:

git clone https://github.com/tgsmith61591/clust4j.git
cd clust4j
./gradlew build ## Go grab some coffee... this takes a minute
## jar is at build/libs/clust4j-x.x.x.jar and includes dependencies

---

clust4j includes some datasets:

Get started quickly with clust4j by loading one of the built-in datasets:

• Iris
  • Predict the species of iris given four features corresponding to petal attributes
• Wine
  • Predict the type of wine given 13 features derived from a chemical analysis
• Breast cancer
  • Predict whether a tumor is benign or malignant given 30 different features, such as "smoothness," "compactness," and "symmetry"

Usage:

DataSet data;
data = ExampleDataSets.loadIris();
data = ExampleDataSets.loadWine();
data = ExampleDataSets.loadBreastCancer();

---

Simple example data (to use for reproducability):

final int k = 2;
final Array2DRowRealMatrix mat = new Array2DRowRealMatrix(new double[][] {
    new double[] {0.005,     0.182751,  0.1284},
    new double[] {3.65816,   0.29518,   2.123316},
    new double[] {4.1234,    0.2301,    1.8900002}
});	

Currently implemented algorithms:

• Partitional algorithms:

  • k-Means, an unsupervised clustering method that aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean (centroid), serving as a prototype of the cluster.

    ```java
    KMeans km = new KMeansParameters(k).fitNewModel(mat);
    final int[] results = km.getLabels();
    ```
    

  • k-Medoids, an unsupervised clustering method that chooses datapoints as centers (medoids or exemplars) and works with an arbitrary matrix of distances between datapoints instead of using the Euclidean norm.

    ```java
    KMedoids km = new KMedoidsParameters(k).fitNewModel(mat);
    final int[] results = km.getLabels();
    ```
    

  • Affinity Propagation, a clustering algorithm based on the concept of "message passing" between data points.Like KMedoids, Affinity Propagation finds "exemplars", members of the input set that are representative of clusters.

    ```java
    AffinityPropagation ap = new AffinityPropagationParameters().fitNewModel(mat);
    final int[] results = ap.getLabels();
    ```
    

• Hierarchical algorithms:

  • HierarchicalAgglomerative, a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy. Agglomerative clustering is not computationally friendly in how it scales. The agglomerative clustering procedure performs at O(n²), but far outperforms its cousin, Divisive Clustering.

    ```java
    HierarchicalAgglomerative a = new HierarchicalAgglomerativeParameters().fitNewModel(mat);
    final int[] results = a.getLabels();
    ```
    

• Density-based algorithms:

  • DBSCAN, a density-based clustering algorithm: given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away).

    ```java
    DBSCAN db = new DBSCANParameters(0.75).fitNewModel(mat);
    final int[] results = db.getLabels();
    ```
    

  • HDBSCAN, a density-based clustering algorithm: performs DBSCAN over varying epsilon values and integrates the result to find a clustering that gives the best stability over epsilon. This implementation includes five algorithms: PrimsKD, PrimsBall, BoruvkaKD and BoruvkaBall.

    ```java
    HDBSCAN hdb = new HDBSCANParameters().fitNewModel(mat);
    final int[] results = hdb.getLabels();
    ```
    

  • MeanShift, a non-parametric feature-space analysis technique for locating the maxima of a density function, a so-called mode-seeking algorithm.

    ```java
    MeanShift ms = new MeanShiftParameters(0.5).fitNewModel(mat);
    final int[] results = ms.getLabels();
    ```
    

• Neighbor point clustering algorithms:

  • NearestNeighbors, a neighbor clusterer that will fit the k-nearest points for each record in a matrix.

    ```java
    NearestNeighbors nn = new NearestNeighborsParameters(k).fitNewModel(mat);
    Neighborhood neighborhood = nn.getNeighbors();
    int[][] indices = neighborhood.getIndices(); // The indices in order of nearness
    double[][] distances = neighborhood.getDistances(); // The corresponding distances
    ```
    

  • RadiusNeighbors, a neighbor clusterer that will fit the nearest points within a given radius.

    ```java
    RadiusNeighbors rn = new RadiusNeighborsParameters(1.5).fitNewModel(mat);
    Neighborhood neighborhood = rn.getNeighbors();
    int[][] indices = neighborhood.getIndices(); // The indices in order of nearness
    double[][] distances = neighborhood.getDistances(); // The corresponding distances
    ```
    

• Supervised clustering algorithms:

  • NearestCentroid, a supervised algorithm that fits centroids based on a set of observed labels.

    ```java
    NearestCentroid nc = new NearestCentroidParameters().fitNewModel(mat, new int[]{0,1,1});
    // you can use .predict(AbstractRealMatrix) to retrieve predicted class labels on new data
    ```
    

Evaluating performance

All clustering algorithms that implement Classifier can also be scored. Supervised and unsupervised methods are scored in different manners. If we want to score the NearestCentroid model we fit above:

// implicitly uses ground truth and predicted labels
double accuracy = nc.score();

Conversely, if we'd like to score an unsupervised algorithm, we have a few options. Every UnsupervisedClassifier implements a silhouetteScore method, but also implements a home-grown scoring algorithm called INDEX_AFFINITY. This operates based on the following complication:

// our k-means model predicts labels like this:
km.getLabels(); // {0,1,1}
// ...but the ground truth may actually be {9,15,15}

... this method, then, is an attempt to measure accuracy not traditionally, but by accounting for predicted segmentation in regards to actual label segmentation. It works by penalizing indices which are inappropriately associated with incorrect neighbor indices. In this regard a ground truth set of {0,1,0,2,2} and predicted set of {2,0,2,1,1} would be 100% accurate. Use as follows:

km.indexAffinityScore(new int[]{50,10,10}); // 100%

Alternatively, the silhouetteScore method can be called as follows:

km.silhouetteScore(); // Uses internally predicted labels

Making predictions

Any algorithm implementing BaseClassifier or its sub-interfaces will implement the method predict(AbstractRealMatrix). After the model has been fit, predictions can be made as follows (using KMeans for example):

KMeans model = new KMeansParameters(2).fitNewModel(mat); // fit the model on the training data
Array2DRowRealMatrix newData = new Array2DRowRealMatrix(new double[][]{ // here's the new data
    new double[]{0.0, 0.0, 0.0},
    new double[]{3.0, 0.0, 2.0}
});
int[] predicted_labels = model.predict(newData); // returns {0, 1}

Note that HDBSCAN does not currently implement a functional predict method, and will throw an UnsupportedOperationException.

Putting it all together with the TrainTestSplit

clust4j includes a TrainTestSplit class that will shuffle and split a DataSet given a training ratio. This can be useful for both SupervisedClassifiers as well as UnsupervisedClassifiers (especially when leveraging clust4j's own proprietary INDEX_AFFINITY as a scoring metric). Here's an example of how this can be used with KMeans:

// Load data, get splits
TrainTestSplit split = new TrainTestSplit(ExampleDataSets.loadIris(), 0.70);
DataSet train = split.getTrain(), test = split.getTest();

// Fit a model and get predictions
KMeans model = new KMeansParameters(3).fitNewModel(train.getData());
int[] predicted_labels = model.predict(test.getData());

// Get the "affinity" score using the Index Affinity algorithm:
double affinity = ClassificationScoring.INDEX_AFFINITY.evaluate(test.getLabels(), predicted_labels)

Put your model into a Pipeline:

clust4j includes a Pipeline object to feed data through a series of ordered PreProcessors and finally, into a clustering model (see below, in the utilities section for more info). Here's an example:

// Let's predict whether a tumor is malignant or benign:
TrainTestSplit split = new TrainTestSplit(ExampleDataSets.loadBreastCancer(), 0.7);

// Get the splits
DataSet training = split.getTrain();
DataSet holdout  = split.getTest();

// Initialize pipe
SupervisedPipeline<NearestCentroid> pipeline = new SupervisedPipeline<NearestCentroid>(
	// This is the parameter class for the model that will be fit
	new NearestCentroidParameters()
		.setVerbose(true)
		.setMetric(new GaussianKernel()),

	// These are the preprocessors that will transform the training data:
	new StandardScaler(), // first transformation
	new MinMaxScaler(),   // second transformation
	new PCA(0.85)         // final transformation
);

// Fit the pipeline:
pipeline.fit(training.getData(), training.getLabels());

// Make predictions:
int[] predicted_labels = pipeline.predict(holdout.getData());

---

Separability metrics

A number of separability metrics are available for use:

• Bray-Curtis distance
• Canberra distance
• Chebyshev distance
• Cosine similarity
• Dice distance
• Euclidean distance (L² norm)
• Kernel similarity methods (descriptions by César Souza^[1])]
• Haversine distance (for geospatial cluster analysis)
• Hamming distance
• Kulsinsky distance
• Manhattan distance (L¹ norm)
• Minkowski distance (L^P norm)
• Rogers-Tanimoto distance
• Russell-Rao distance
• Sokal-Sneath distance
• Yule distance

---

Kernel functions:

• ANOVA kernel, a radial basis function kernel, just as the Gaussian and Laplacian kernels. It is said to perform well in multidimensional regression problems (Hofmann, 2008).

• Cauchy kernel, a long-tailed kernel and can be used to give long-range influence and sensitivity over the high dimension space.

• Circular kernel, an example of an isotropic stationary kernel that is positive definite in R².

• Exponential kernel; closely related to the Gaussian kernel, with only the square of the norm left out. It is also a radial basis function kernel.

• Gaussian kernel, an example of radial basis function kernel. The adjustable parameter sigma plays a major role in the performance of the kernel, and should be carefully tuned to the problem at hand. If overestimated, the exponential will behave almost linearly and the higher-dimensional projection will start to lose its non-linear power. In the other hand, if underestimated, the function will lack regularization and the decision boundary will be highly sensitive to noise in training data.

• Hyperbolic Tangent (sigmoid/tanh) kernel, also known as the Sigmoid Kernel and as the Multilayer Perceptron (MLP) kernel. The Sigmoid Kernel comes from the Neural Networks field, where the bipolar sigmoid function is often used as an activation function for artificial neurons.

• Laplacian kernel; completely equivalent to the exponential kernel, except for being less sensitive for changes in the sigma parameter. Being equivalent, it is also a radial basis function kernel.

• Linear kernel, the simplest kernel function. It is given by the inner product <x,y> plus an optional constant c.

• Log kernel; seems to be particularly interesting for images, but is only conditionally positive definite.

• Multiquadric (and Inverse Multiquadric) kernel; can be used in the same situations as the Rational Quadratic kernel. In the case of the Inverse Multiquadric Kernel, it results in a kernel matrix with full rank (Micchelli, 1986) and thus forms a infinite dimension feature space.

• Polynomial kernel, a non-stationary kernel. Polynomial kernels are well suited for problems where all the training data is normalized.

• Power kernel, also known as the (unrectified) triangular kernel. It is an example of scale-invariant kernel (Sahbi and Fleuret, 2004) and is also only conditionally positive definite.

• Radial Basis kernel, commonly used in support vector machine classification, the Radial Basis Function Kernel (RBF) may be recognized as the squared Euclidean distance between the two feature vectors where sigma is a free parameter. The feature space of the kernel has an infinite number of dimensions.

• Rational Quadratic kernel; less computationally intensive than the Gaussian kernel and can be used as an alternative when using the Gaussian becomes too expensive.

• Spherical kernel, similar to the circular kernel, but is positive definite in R³.

• Spline kernel, given as a piece-wise cubic polynomial, as derived in the works by Gunn (1998).

---

Notice the differentiation between similarity-based and distance-based geometrically separable metrics. All the clustering algorithms are able to handle any metric implementing the GeometricallySeparable interface. Since SimilarityMetric's getSimilarity(...) method should return the negative of getDistance(...), separability metrics implementing SimilarityMetric implicitly will attempt to maximize similarity (as all clustering algorithms will minimize distance). Classes implementing SimilarityMetric should define the getDistance(double[], double[]) method to return -getSimilarity(double[], double[]).

When to use similarity metrics over distance metrics?

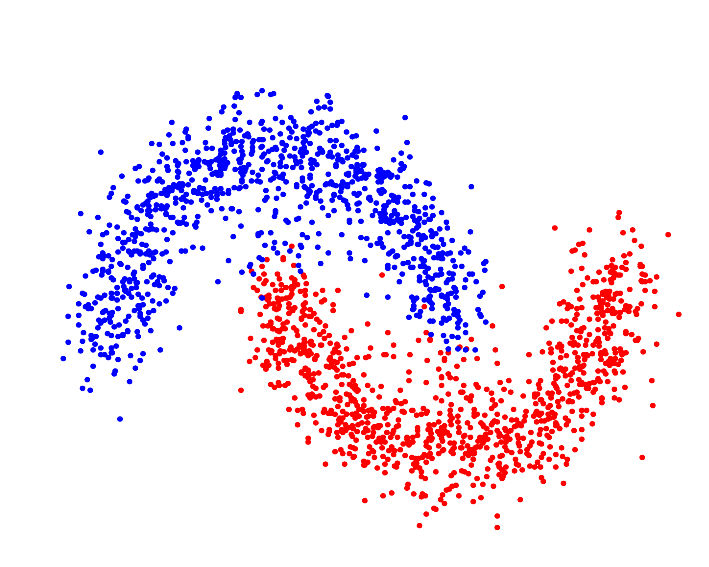
Various similarity metrics—kernel methods, in particular—allow the clustering algorithm to segment the data in Hilbert Space^[4], which can—assuming the proper kernel is selected—allow the algorithm to identify "complex," or non-(hyper)spherically shaped clusters:

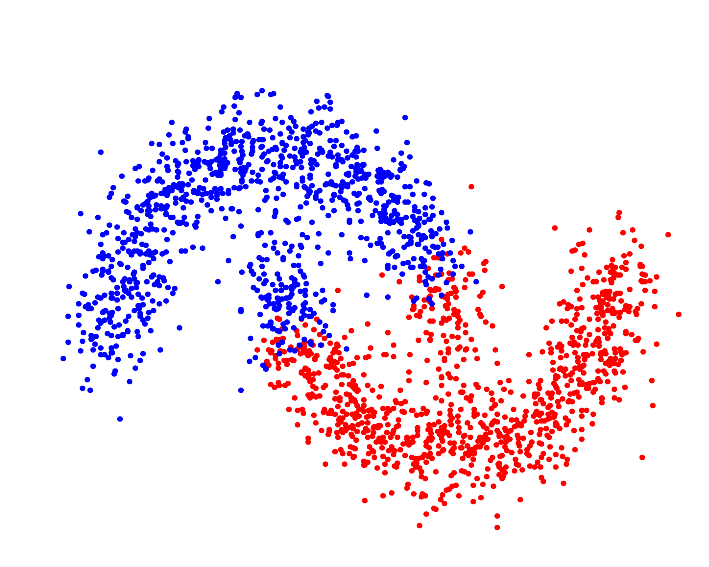
Whereas a distance metric in Euclidean space may struggle with oddly shaped clusters^[9]:

To initialize any clusterer with a kernel as the GeometricallySeparable metric (example uses GaussianKernel):

final Kernel kernel = new GaussianKernel();
KMedoids km = new KMedoids(mat, new KMedoidsPlanner(k).setSep(kernel));

Note: though similarity metrics may be used with any clustering algorithm, it is recommended that they not be used with density-based clustering algorithms, as they seek "neighborhoods" around points and similarity metrics such as kernels will not accurately describe a point's neighborhood. Using a similarity metric with a density-based algorithm will cause a warning to be logged and the algorithm will fall back to the default separability metric (Euclidean distance).

---

Utilities

• Matrix imputation:

  • Mean imputation
  • Median imputation
  • Bootstrap (basic or smooth) imputation
  • KNN Imputation

• Pipeline:

  • Construct a pipeline of PreProcessors through which to push new data, resulting in a cluster fit:

    ```java
    // Unsupervised:
    final KMedoidsParameters planner = new KMedoidsParameters(2).setVerbose(true);
    // Use of varargs for the PreProcessors is supported
    final UnsupervisedPipeline<KMedoids> pipe = new UnsupervisedPipeline<KMedoids>(planner, new StandardScaler() /*, ... */);
    // Push data through preprocessing pipeline and fit model
    KMedoids km = pipe.fit(mat);
    
    // Supervised:
    final NearestCentroidParameters s_planner = new NearestCentroidParameters().setVerbose(true);
    final SupervisedPipeline<NearestCentroid> sup_pip = new SupervisedPipeline<NearestCentroid>(s_planner, new StandardScaler());
    NearestCentroid model = sup_pip.fit(mat, new int[]{0,1,1});
    ```
    

---

Things to note:

• Note that normalization is recommended prior to clustering. Example on a KMeans constructor:

  // For normalization, simply use a `PreProcessor`:
  PreProcessor p = new StandardScaler().fit(X);
  KMeans km = new KMeansParameters(k).fitNewModel(p.transform(X));

• By default, logging is disabled. This can be enabled by instance in any BaseClustererParameters class by invoking .setVerbose(true).

• Note that the default setting may be set globally:

  AbstractClusterer.DEF_VERBOSE = true;

---

References:

1. Souza C.R., Kernel Functions for Machine Learning
2. Yu K., Ji L., Zhang X., Kernel Nearest-Neighbor Algorithm
3. Ester M., Kriegel H.-P., Sander J.S., Xu X., 1996. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise, Institute for Computer Science, University of Munich
4. Chitta, R., Kernel Clustering
5. kernlab R package
6. h2o (for log wrapper structure)
7. Divisive Clustering
8. sklearn clustering repository
9. The Drawbacks of k-Means
10. hdbscan python implementation
11. HDBSCAN research paper