Simple, small sized implementation of select algorithms in C++
Used for traversing a graph
G is the adjacency matrix representing the graph.
'visited' array marks nodes as visited.
bfs(v):
- Mark 'v' as visited and print it
- For each node in G connected to 'v' and unvisited, mark node as visited and add it to the queue
- For each node 't' in the queue call bfs(t)
Used for traversing a graph
G is the adjacency matrix representing the graph.
'visited' array marks nodes as visited.
dfs(v):
- Mark 'v' as visited and print it
- For each node 't' in G connected to 'v' and unvisited, mark node as visited and call dfs(t)
Used to find shortest path from a source to all other nodes
G is the adjacency matrix representing the graph (999 represents ∞).
'v' is the source node from which shortest distance is computed.
'visited' array marks nodes as visited.
'dist' holds shortest distances from the source node.
- Update distance array with distances from the source node (with values from the graph)
- Mark source node as visited
- Find nearest unvisited node 'u' from source
- For every node 'k' in the graph, check if distance from source to 'k' is less than sum of distances from source to 'u' and 'u' to 'k'
- If not, update distance to the new minimum
- Repeat from step 3 until all nodes are marked as visited
Used to find shortest paths for all pairs of nodes
G is the adjacency matrix representing the graph (999 represents ∞).
'dist' matrix holds the shortest distance values.
- Initialize dist with G
- Consider each node 'i' in the graph as an intermediate node
- For every pair of vertices 'j' and 'k', check if distance from 'j' to 'k' is shorter than sum of distances from 'j' to 'i' and 'i' to 'k'
- If not, update dist with the minimum value
Used to find minimum spanning tree
G is the adjacency matrix representing the graph (999 represents ∞).
'parent' is used to keep track of connected nodes and check for loops.
- Find the shortest edge in the graph. Call the nodes 'u' and 'v'
- Check if 'u' and 'v' are connected by a common parent
- If not, select the edge, update the cost, and set 'u' as parent of 'v'
- Repeat from step 1 till n-1 edges are found (n is number of nodes in the graph)
For a given NxN chess board, find the ways in which N queens can be placed so that no two queens share the same row, column or diagonal
'col' array holds the column numbers(of successive rows) where queen can be placed.
nq(N, k):
- For given row 'k', check each column if queen can be placed
- If yes, update col and call nq(N, k+1)
- If last row has been reached, display 'col'
- Repeat step 1 for each row
Used to find minimum spanning tree
G is the adjacency matrix representing the graph (999 represents ∞).
'visited' array marks nodes as visited.
- Mark first node as visited
- Find the nearest unvisited node from any of the visited nodes
- Mark it as visited
- Repeat from step 2 till all nodes are visited
For a given set of integers, check if there exists a subset of it such that the sum of its integers equals a given value M
M is the value of the sum
'val' array holds the given integer set in ascending order, along with a large integer as the last element. This is to avoid checking for end of array
'selected' marks elements that are to be taken
sumofsub(sum, k):
- Mark element k as selected, and check if including it gives M
- If yes, display selected items
- Else, if including current and next element can give M, call sumofsub(sum+val[k], k+1)
- Check if leaving out current element can give M, call sumofsub(sum, k+1)
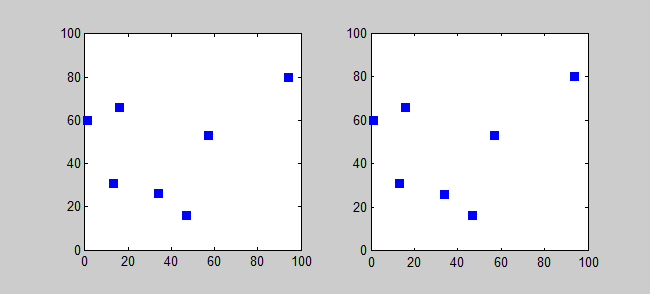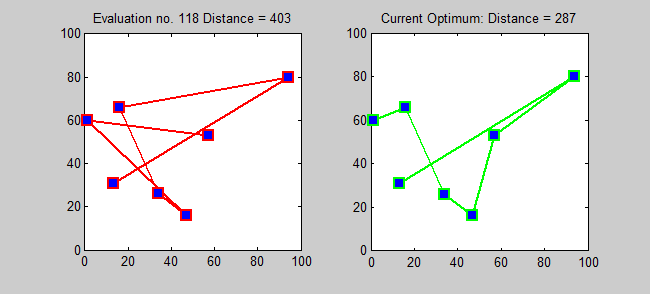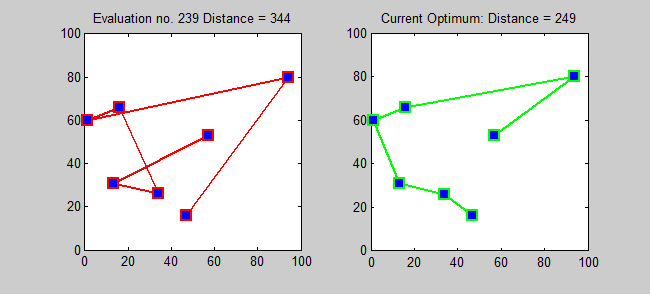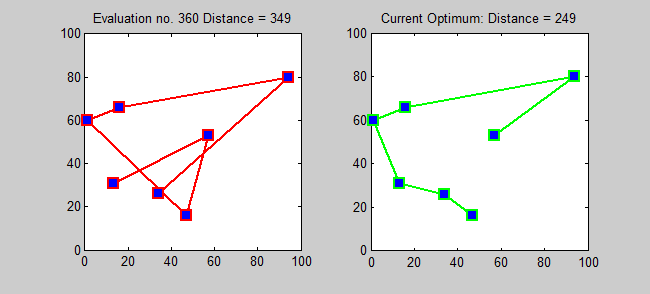
For a given a list of cities and the distances between each pair of cities, find the shortest possible route that visits each city exactly once and returns to the origin city
'tour_brute' and 'cost_brute' represent the final tour and cost respectively.
'v' array holds the route that is currently being tested.
tsp_brute(cur):
- If last node has been reached, find cost of current route
- If this cost is the smallest so far, copy 'v' to 'tour_brute'
- If not last node, for each of the remaining nodes:
a. swap with current node in 'v'
b. call tsp_brute(cur+1)
c. restore values by swapping back