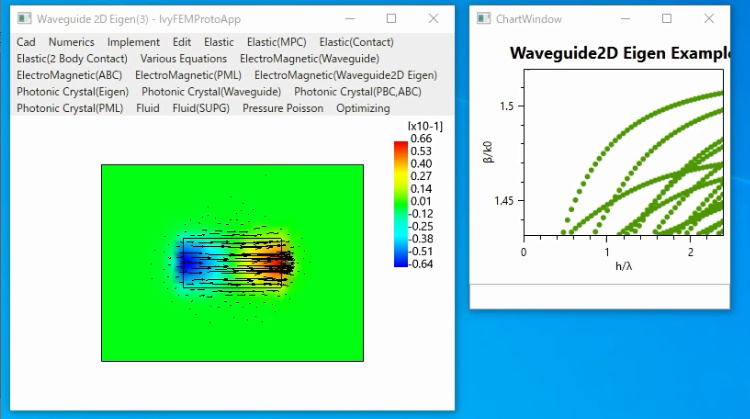
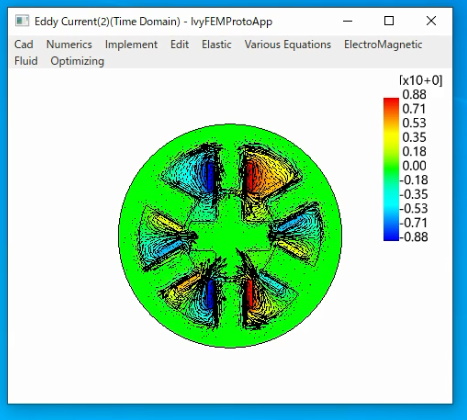
有限要素法(FEM)を用いたCAEライブラリです。
.Net WPFアプリケーションで使用することを想定しています。
いまできること
☑ 2D(多角形)、3D(限定的)の図面作成
☑ 有限要素(三角形要素、四面体要素※)分割
☑ 有限要素行列の作成 (*1)
☑ リニアシステムを解く(LAPACKE, Lis、独自実装)
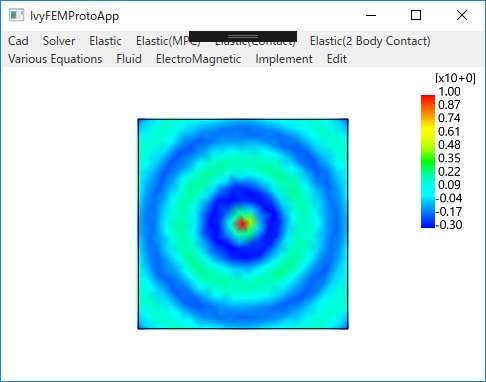
☑ サーモグラフィーのような分布図
*1 いま用意しているのは
弾性体力学:線形弾性体(2D/3D)
超弾性体
St.Venant Kirchhoff(2D/3D)
Mooney-Rivlin (非圧縮、微圧縮)(2D/3D)
Ogden (非圧縮、微圧縮)(2D/3D)
多点拘束(Multipoint Constraint [MPC])(2D:直線/3D:平面)
剛体との接触(2D:直線、円/3D:平面、球)
弾性体二体接触(2D/3D)※
構造要素(線形)
Truss要素(トラス)
Beam要素(X方向の梁)(非推奨)
Euler-Bernoulli
Timoshenko
Frame要素(骨組、方向の異なるトラス/梁を繋いだもの)
Euler-Bernoulli
Timoshenko
DKT薄板要素(Discrete Kirchhoff Flat Plates)
Mindlin厚板要素(Reisner-Mindlin Thick Plates)
MITC3シェル要素(MITC: Mixed Interpolation of Tensorial Components)
構造要素(幾何学的非線形)
Co-rotational Beam(Frame) Formulation
Euler-Bernoulli shallow arch
Timoshenko Beam(Frame)
Total Lagrange法
Eular-Bernoulli Field-consistent Beam(Frame)
Timoshenko Beam(Frame)
MITC3シェル要素
St.Venant-Kirchhoff
St.Venant-Kirchhoff(厚さの伸び縮み考慮)
Mooney-Rivlin超弾性体モデル(厚さの伸び縮み考慮)
弾性波プレート導波路(elastic plate waveguides)
Lamb waveの固有値問題(1D)
Lamb waveの伝達問題(2D)
周波数領域FEM
(固有モード展開)
(PML: Perfectly Matched Layers,完全整合層)
(ABC: Absorbing Boundary Conditions,吸収境界条件)
時間領域FEM
(PML: Perfectly Matched Layers,完全整合層)
SH waveの固有値問題(1D)
SH waveの伝達問題(2D)
周波数領域FEM
(固有モード展開)
(PML: Perfectly Matched Layers,完全整合層)
(ABC: Absorbing Boundary Conditions,吸収境界条件)
Note: SH wave:Shear Horizontal wave
流体力学 :Navier-Stokesの方程式
標準(2D/3D)(ただし、3Dは※)
SUPG [Streamline Upwind Petrov-Galerkin]安定化(2D/3D)
Vorticity / Stream Funciton定式化
標準
SUPG[Streamline Upwind Petrov-Galerkin]安定化※
分離型解法(Runge-Kutta)(標準)
Pressure Poisson定式化※
標準
SUPG[Streamline Upwind Petrov-Galerkin]安定化※
分離型解法(Runge-Kutta)(標準)
分離型解法(Runge-Kutta)(SUPG[Streamline Upwind Petrov-Galerkin]安定化)※
Finite Calculus (FIC) Formulation
RANS(Reynolds Average Navier Stokes) 定式化
RNG k-epsilonモデル
LES(Large Eddy Simulation)※
k equation model
乱流(turbulent)中の滴(droplet)の軌跡※
電磁気学 :電磁導波路の伝達問題(2D)
H面TEモード/E面TEモード/2次元TMモードの導波路
周波数領域FEM
(固有モード展開)
(Givoli-Neta-Patlashenkoの高次ABC)(Evanescent Wave ABC)
(PML)
時間領域FEM
(Givoli-Neta-Patlashenkoの高次ABC)(Evanescent Wave ABC)
(Jiao-Jin-Michielssen-RileyのPML)
フォトニック結晶の固有値問題
正方格子、三角形格子
誘電体ロッド型、エアホール型
フォトニックバンドギャップ
フォトニック結晶導波路
フォトニック結晶導波路の伝達問題
正方格子、三角形格子
誘電体ロッド型、エアホール型
周波数領域FEM
(固有モード展開)
(PBC)
(PML)
時間領域FEM
(Jiao-Jin-Michielssen-RileyのPML)
(固有モード展開複素ABC(Modal ABCZ))※
full-wave(ベクトル波)導波路の固有値問題
edge/nodal elements
(遮蔽形, closed waveguides)
(開放形, open or unbounded waveguides)
共振器の固有値問題(3D)
電磁導波路の伝達問題(3D)
周波数領域FEM
(固有モード展開)
Note: ABC - Absorbing Boundary Conditions, 吸収境界条件
PML - Perfectly Matched Layers, 完全整合層
PBC - Periodic Boundary Conditions, 周期境界条件
渦電流(eddy current)場問題
A-φ法(2D)
各種方程式:Poisson方程式(2D/3D)
熱拡散方程式(2D/3D)
移流拡散方程式(2D/3D)
Helmholtz方程式(2D/3D)
三角形要素:Lagrange (1次、2次)
Bell Triangle(5次)
edge element(1次、2次)
四面体要素:Lagrange (1次、2次)
edge element(1次、2次)
※印:実験的または未完
バイナリ(2021-06-30更新)
IvyFEM.dll version 0.0.0.63
プラットフォームターゲット: x64
IvyFEM
依存ライブラリ
OpenTK.GLControlをNuGetでインストールしてください。
インストールおよび使い方
インストール、実装概略を次のページにまとめました。
.NET向けCAEライブラリIvyFEMを用いて弾性体の曲げの有限要素法シミュレーションをする
.NET向け有限要素法CAEライブラリIvyFEMでカスタマイズ方程式を実装する
IvyFEM(.NET向け有限要素法ライブラリ)をPythonから使用する
技術資料
定式化をpdfにまとめています。
pdf置き場
サンプルアプリケーション
IvyFEM.dllを使ったサンプルアプリケーション
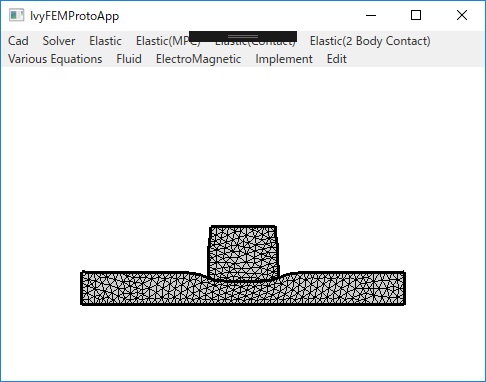
IvyFEMProtoApp
計算例
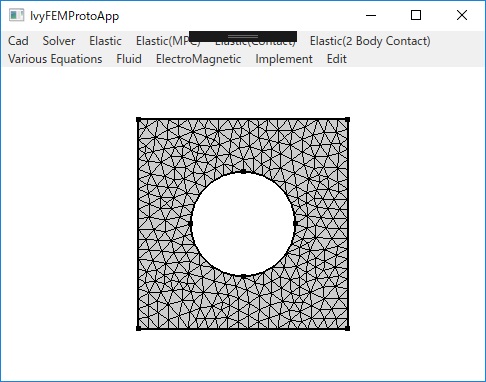
〇メッシュ
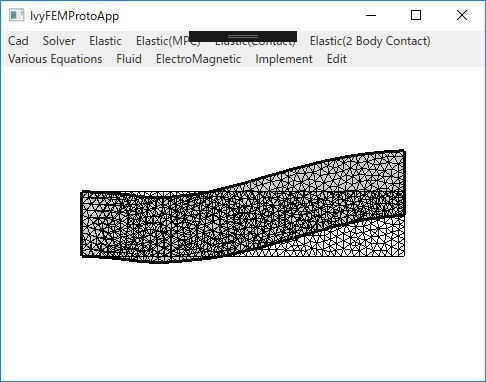
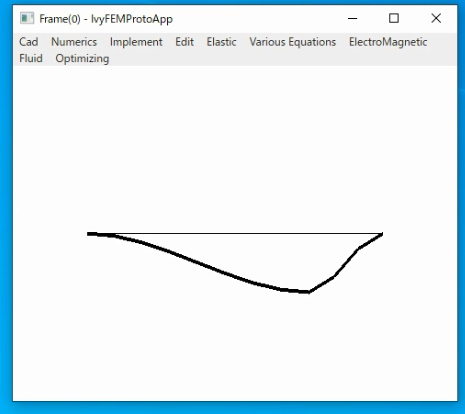
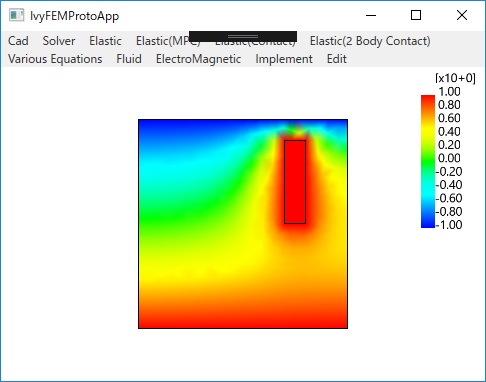
〇弾性体
〇弾性体多点拘束(MPC)
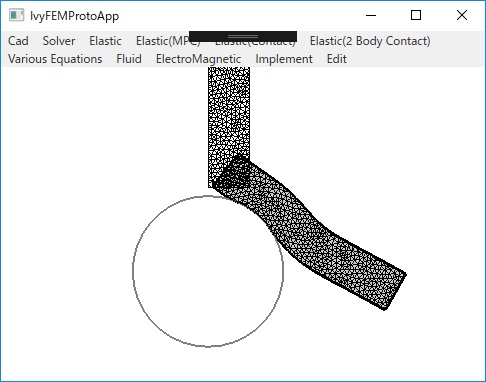
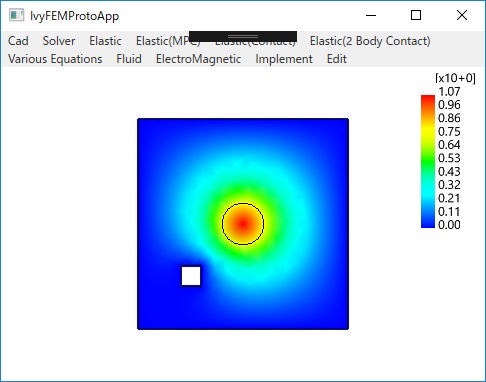
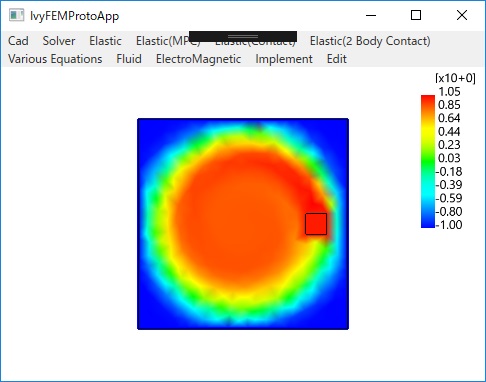
〇直線、円との接触問題
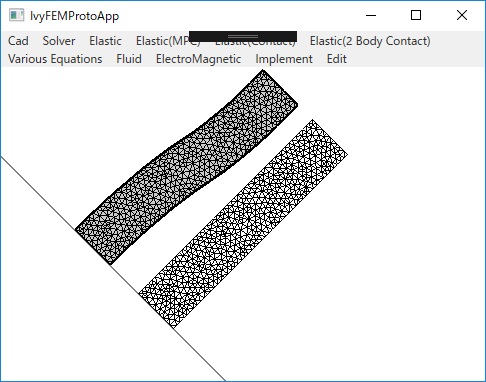
〇弾性体二体接触問題
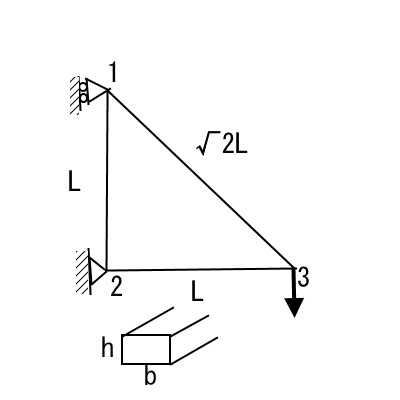
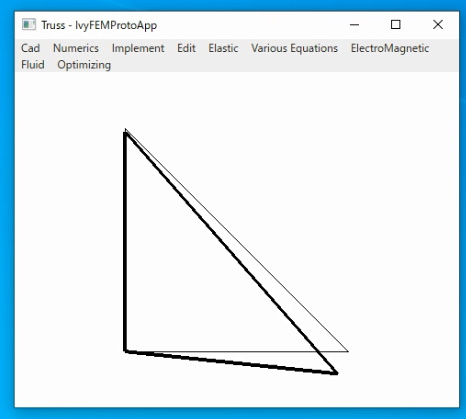
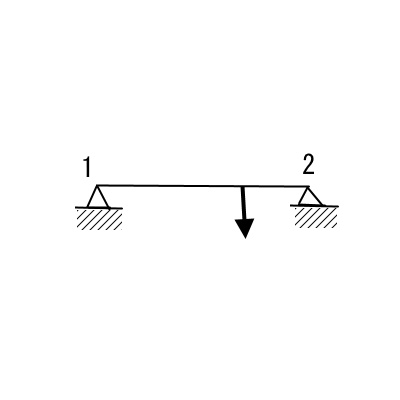
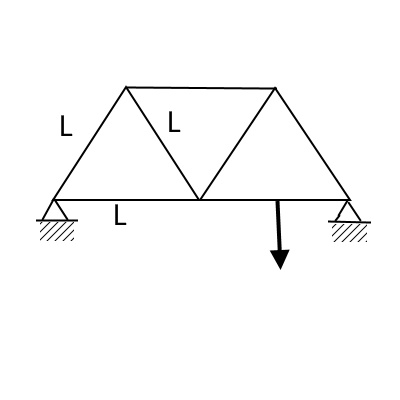
〇構造要素
トラス要素
ビーム要素
フレーム要素
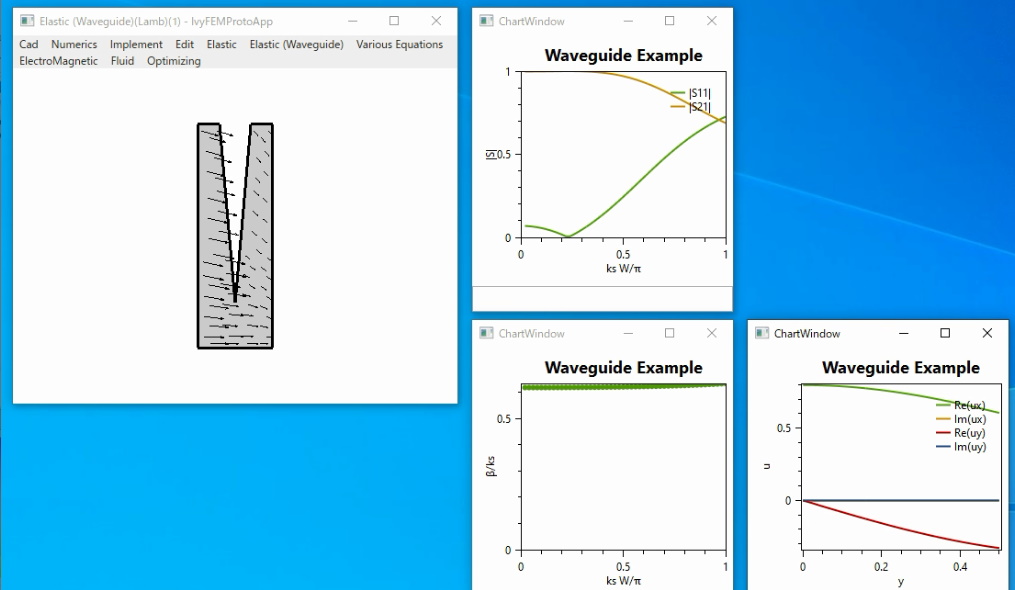
〇弾性波プレート導波路の伝達問題
Lamb wave
〇Poissonの方程式
〇Helmholtzの方程式
〇拡散方程式
〇移流拡散方程式
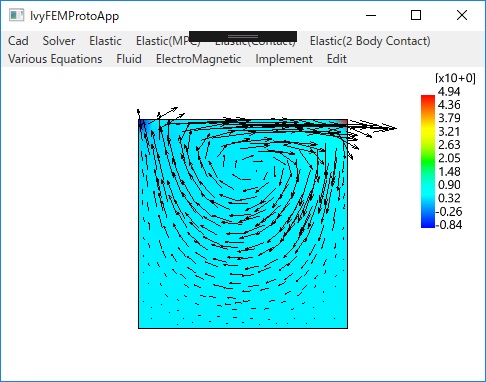
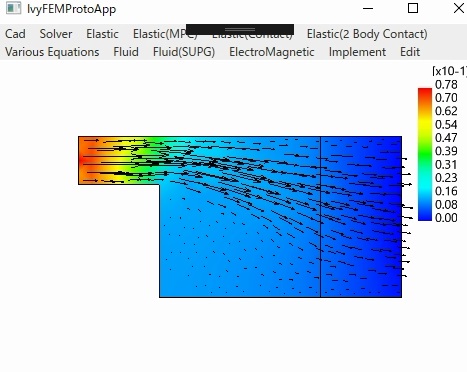
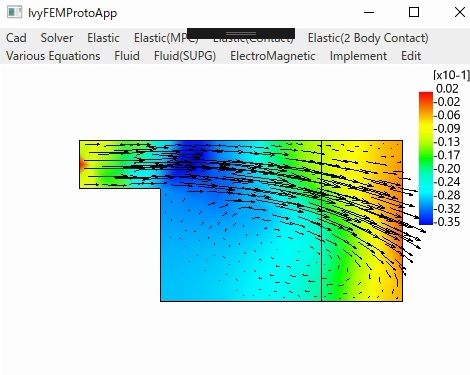
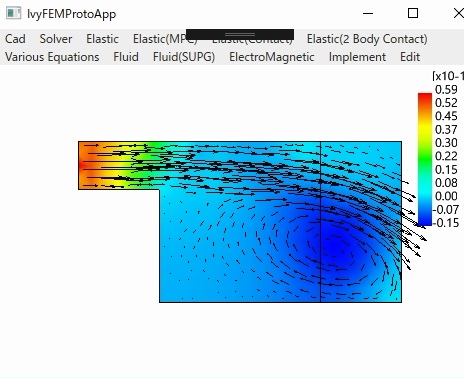
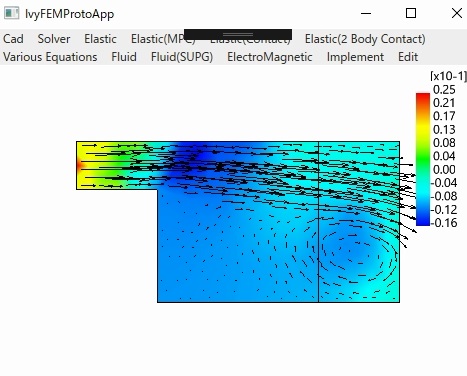
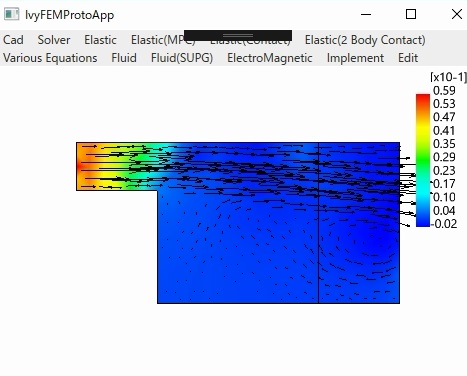
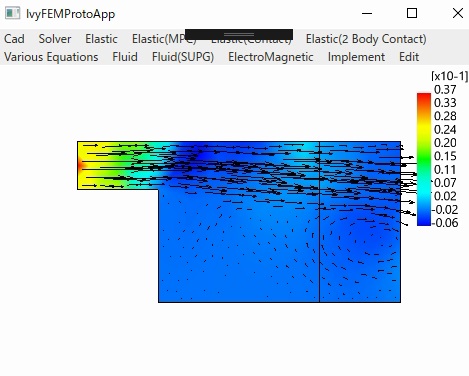
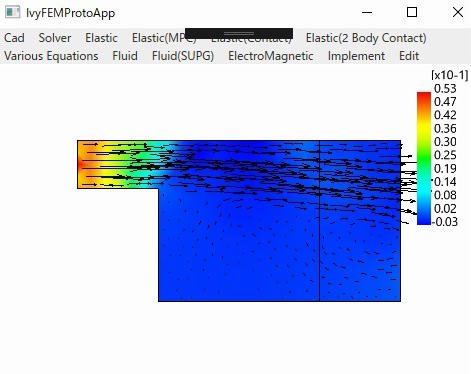
〇流体(Navier-Stokesの方程式)
Standard Galerkin Cavity
SUPG Cavity
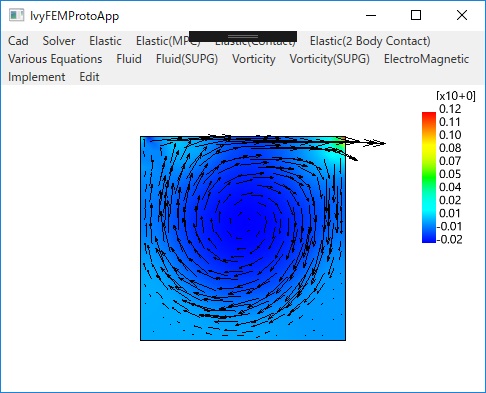
〇流体(Finite Calculus (FIC) Formulation)
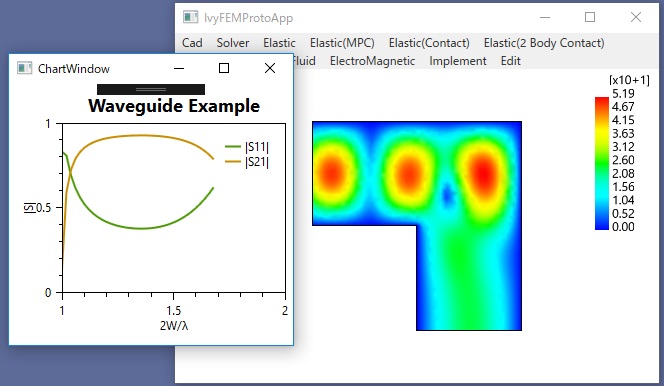
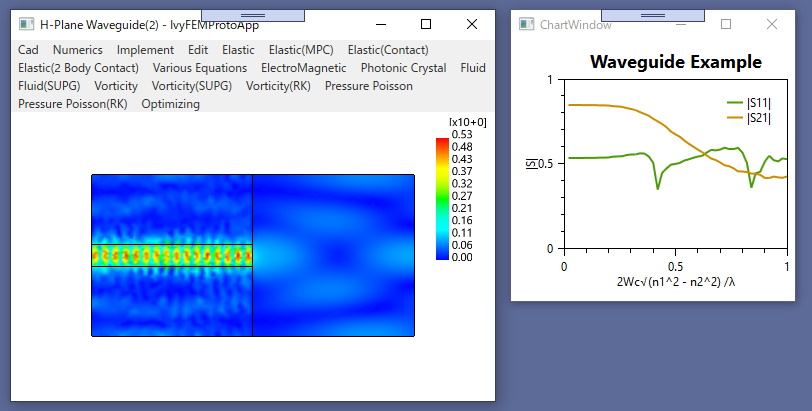
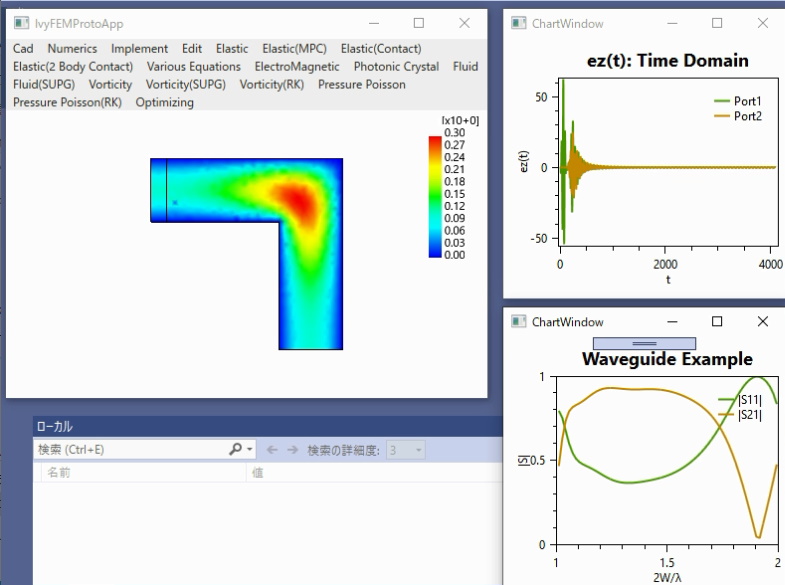
〇電磁導波路の周波数領域FEM(固有モード展開)
H面導波路直角コーナーベンド
遮蔽形誘電体導波路の終端
〇電磁導波路の周波数領域FEM(高次ABC)
開放形誘電体導波路の終端
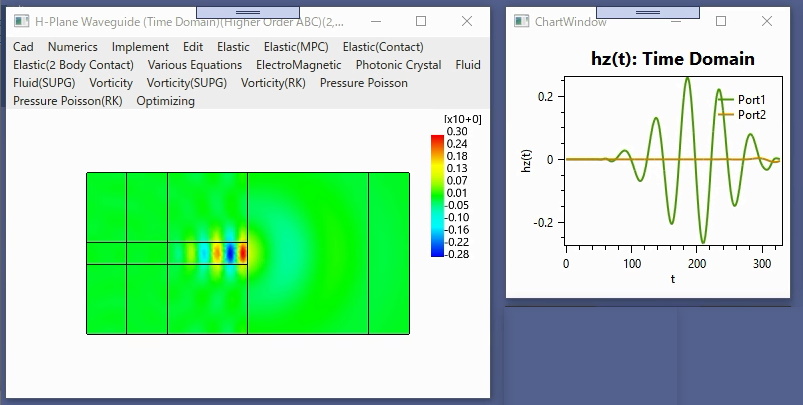
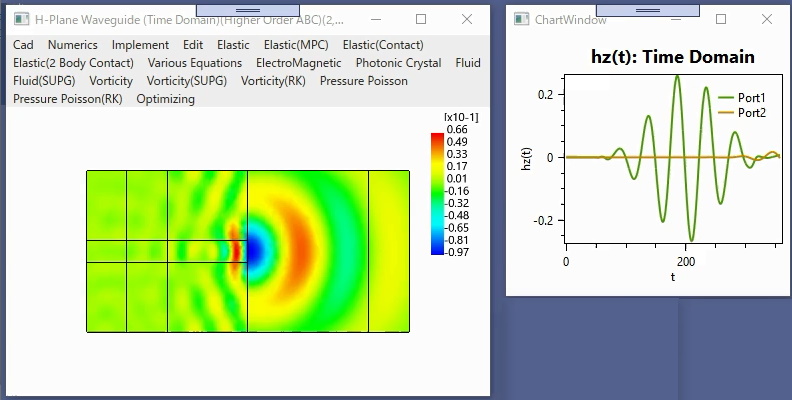
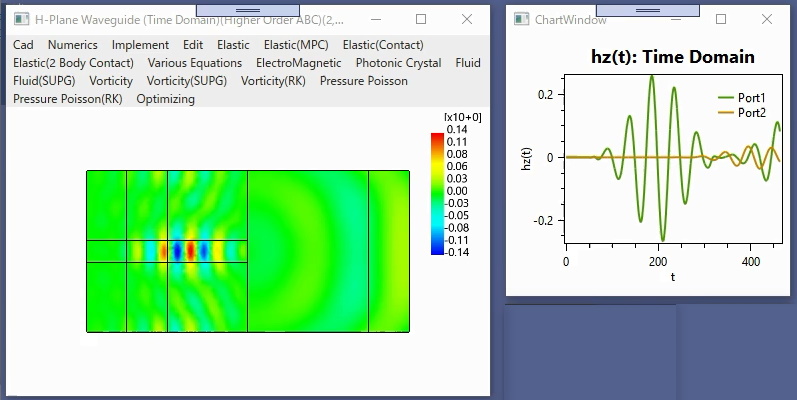
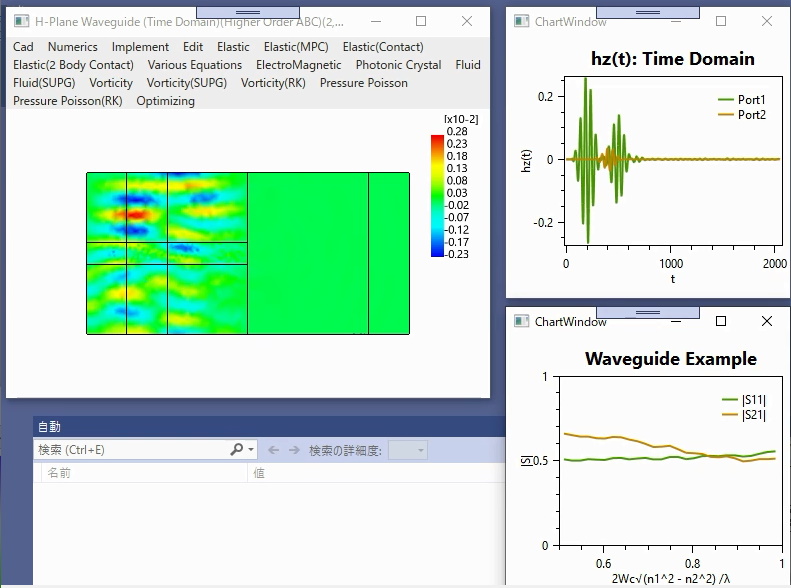
〇電磁導波路の時間領域FEM(高次ABC)
H面導波路直角コーナーベンド
開放形誘電体導波路の終端
〇フォトニックバンドギャップ
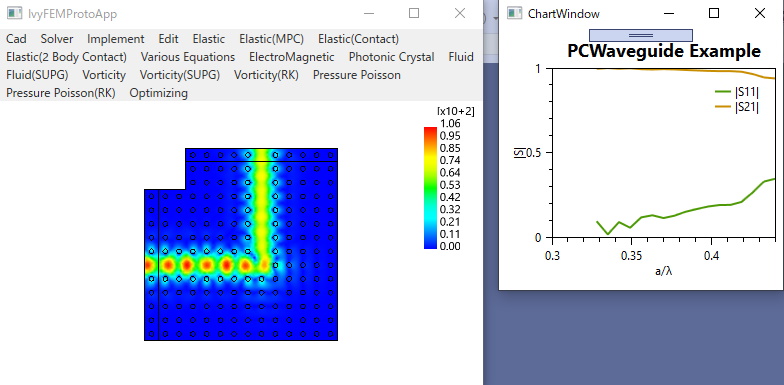
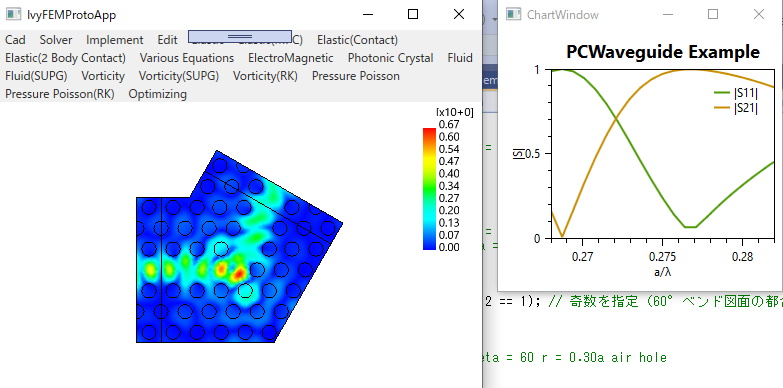
〇フォトニック結晶導波路の周波数領域FEM(固有モード展開)
〇電磁導波路のベクトル波固有モード(full-wave eigenmode)
〇3次元電磁導波路の伝達問題
〇渦電流(eddy current)場
forked from ryujimiya/IvyFEM
-
Notifications
You must be signed in to change notification settings - Fork 0
.NET向け有限要素法(FEM)を用いたCAEライブラリ
License
loading00123/IvyFEM
Folders and files
| Name | Name | Last commit message | Last commit date | |
|---|---|---|---|---|
Repository files navigation
About
.NET向け有限要素法(FEM)を用いたCAEライブラリ
Resources
License
Stars
Watchers
Forks
Languages
- C# 100.0%