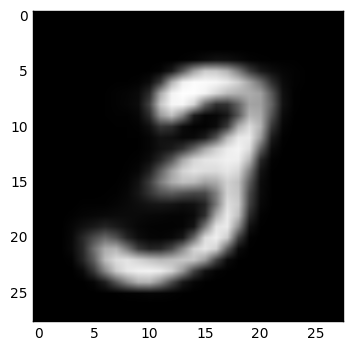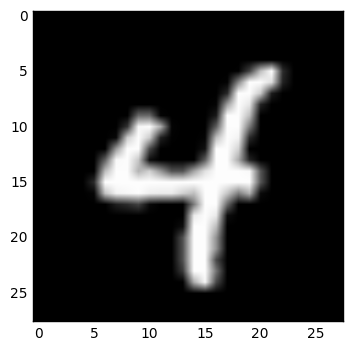tensorflow-rbm

Tensorflow implementation of Restricted Boltzmann Machine.

Overview

This is a fork of https://github.com/meownoid/tensorfow-rbm with some improvements:

• predict function
• notebooks showing several RBM usages:
  • calculate xor with RBM
  • reconstruct images with RBM

Original README

Overview

This is a fork of https://github.com/Cospel/rbm-ae-tf with some corrections and improvements:

• scripts are in the package now
• implemented momentum for RBM
• using probabilities instead of samples for training
• implemented both Bernoulli-Bernoulli RBM and Gaussian-Bernoulli RBM

BBRBM Example

Bernoulli-Bernoulli RBM is good for Bernoulli-distributed binary input data. MNIST, for example.

Load data and train RBM:

import numpy as np
import matplotlib.pyplot as plt
from tfrbm import BBRBM, GBRBM
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
mnist_images = mnist.train.images

bbrbm = BBRBM(n_visible=784, n_hidden=64, learning_rate=0.01, momentum=0.95, use_tqdm=True)
errs = bbrbm.fit(mnist_images, n_epoches=30, batch_size=10)
plt.plot(errs)
plt.show()

Output:

Epoch: 0: 100%|##########| 5500/5500 [00:07<00:00, 743.34it/s]
Train error: 0.1268

Epoch: 1: 100%|##########| 5500/5500 [00:07<00:00, 760.61it/s]
Train error: 0.0847

Epoch: 2: 100%|##########| 5500/5500 [00:07<00:00, 763.98it/s]
Train error: 0.0770

Epoch: 3: 100%|##########| 5500/5500 [00:07<00:00, 767.36it/s]
Train error: 0.0706

Epoch: 4: 100%|##########| 5500/5500 [00:07<00:00, 720.42it/s]
Train error: 0.0645

Epoch: 5: 100%|##########| 5500/5500 [00:07<00:00, 741.36it/s]
Train error: 0.0594

Epoch: 6: 100%|##########| 5500/5500 [00:07<00:00, 739.19it/s]
Train error: 0.0556

Epoch: 7: 100%|##########| 5500/5500 [00:08<00:00, 686.20it/s]
Train error: 0.0527

Epoch: 8: 100%|##########| 5500/5500 [00:09<00:00, 582.32it/s]
Train error: 0.0504

Epoch: 9: 100%|##########| 5500/5500 [00:10<00:00, 549.63it/s]
Train error: 0.0485

...

Examine some reconstructed data:

IMAGE = 1

def show_digit(x):
    plt.imshow(x.reshape((28, 28)), cmap=plt.cm.gray)
    plt.show()

image = mnist_images[IMAGE]
image_rec = bbrbm.reconstruct(image.reshape(1,-1))

show_digit(image)
show_digit(image_rec)

Examples:

API

rbm = BBRBM(n_visible, n_hidden, learning_rate=0.01, momentum=0.95, err_function='mse', use_tqdm=False)

or

rbm = GBRBM(n_visible, n_hidden, learning_rate=0.01, momentum=0.95, err_function='mse', use_tqdm=False, sample_visible=False, sigma=1)

Initialization.

• n_visible — number of neurons on visible layer
• n_hidden — number of neurons on hidden layer
• use_tqdm — use tqdm package for progress indication or not
• err_function — error function (it's not used in training process, just in get_err function), should be mse or cosine

Only for GBRBM:

• sample_visible — sample reconstructed data with Gaussian distribution (with reconstructed value as a mean and a sigma parameter as deviation) or not (if not, every gaussoid will be projected into a single point)
• sigma — standard deviation of the input data

Advices:

• Use BBRBM for Bernoulli distributed data. Input values in this case must be in the interval from 0 to 1.
• Use GBRBM for normal distributed data with 0 mean and sigma standard deviation. If it's not, just normalize it.

rbm.fit(data_x, n_epoches=10, batch_size=10, shuffle=True, verbose=True)

Fit the model.

• data_x — data of shape (n_data, n_visible)
• n_epoches — number of epoches
• batch_size — batch size, should be as small as possible
• shuffle — shuffle data or not
• verbose — output to stdout

Returns errors array.

rbm.partial_fit(batch_x)

Fit the model on one batch.

rbm.reconstruct(batch_x)

Reconstruct data. Input and output shapes are (n_data, n_visible).

rbm.transform(batch_x)

Transform data. Input shape is (n_data, n_visible), output shape is (n_data, n_hidden).

rbm.transform_inv(batch_y)

Inverse transform data. Input shape is (n_data, n_hidden), output shape is (n_data, n_visible).

rbm.get_err(batch_x)

Returns error on batch.

rbm.get_weights()

Get RBM's weights as a numpy arrays. Returns (W, Bv, Bh) where W is weights matrix of shape (n_visible, n_hidden), Bv is visible layer bias of shape (n_visible,) and Bh is hidden layer bias of shape (n_hidden,).

Note: when initializing deep network layer with this weights, use W as weights, Bh as bias and just ignore the Bv.

rbm.set_weights(w, visible_bias, hidden_bias)

Set RBM's weights as numpy arrays.

rbm.save_weights(filename, name)

Save RBM's weights to filename file with unique name prefix.

rbm.load_weights(filename, name)

Loads RBM's weights from filename file with unique name prefix.

Original README

Tensorflow implementation of Restricted Boltzman Machine and Autoencoder for layerwise pretraining of Deep Autoencoders with RBM. Idea is to first create RBMs for pretraining weights for autoencoder. Then weigts for autoencoder are loaded and autoencoder is trained again. In this implementation you can also use tied weights for autoencoder(that means that encoding and decoding layers have same transposed weights!).

I was inspired with these implementations but I need to refactor them and improve them. I tried to use also similar api as it is in tensorflow/models:

myme5261314

saliksyed

Thank you for your gists!

More about pretraining of weights in this paper:

Reducing the Dimensionality of Data with Neural Networks

Feel free to make updates, repairs. You can enhance implementation with some tips from:

Practical Guide to training RBM