The objective of the ChOp project is to design and implement large-scale exact distributed optimization algorithms taking into account CPU-GPU heterogeneity, but also achieving high productivity and parallel efficiency. The prototypes are programmed to enumerate all feasible and complete configurations of the N-Queens. The final versions of the distributed algorithms solve to the optimality instances of combinatorial optimization problems, such as the flow-shop scheduling and the ATSP. This study is pioneering within the context of parallel exact optimization.
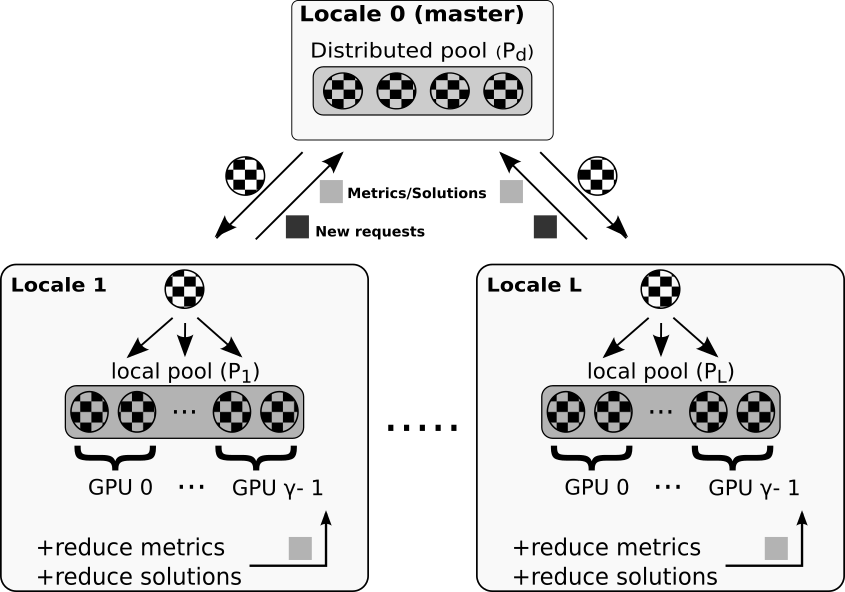
The locale 0 (master) is responsible for generating the distribute pool Pd and controlling the search. Each worker locale receives nodes from the master and generates a local pool that is partitioned into CPU and GPU portions. L locales are launched on L-1 computer nodes.
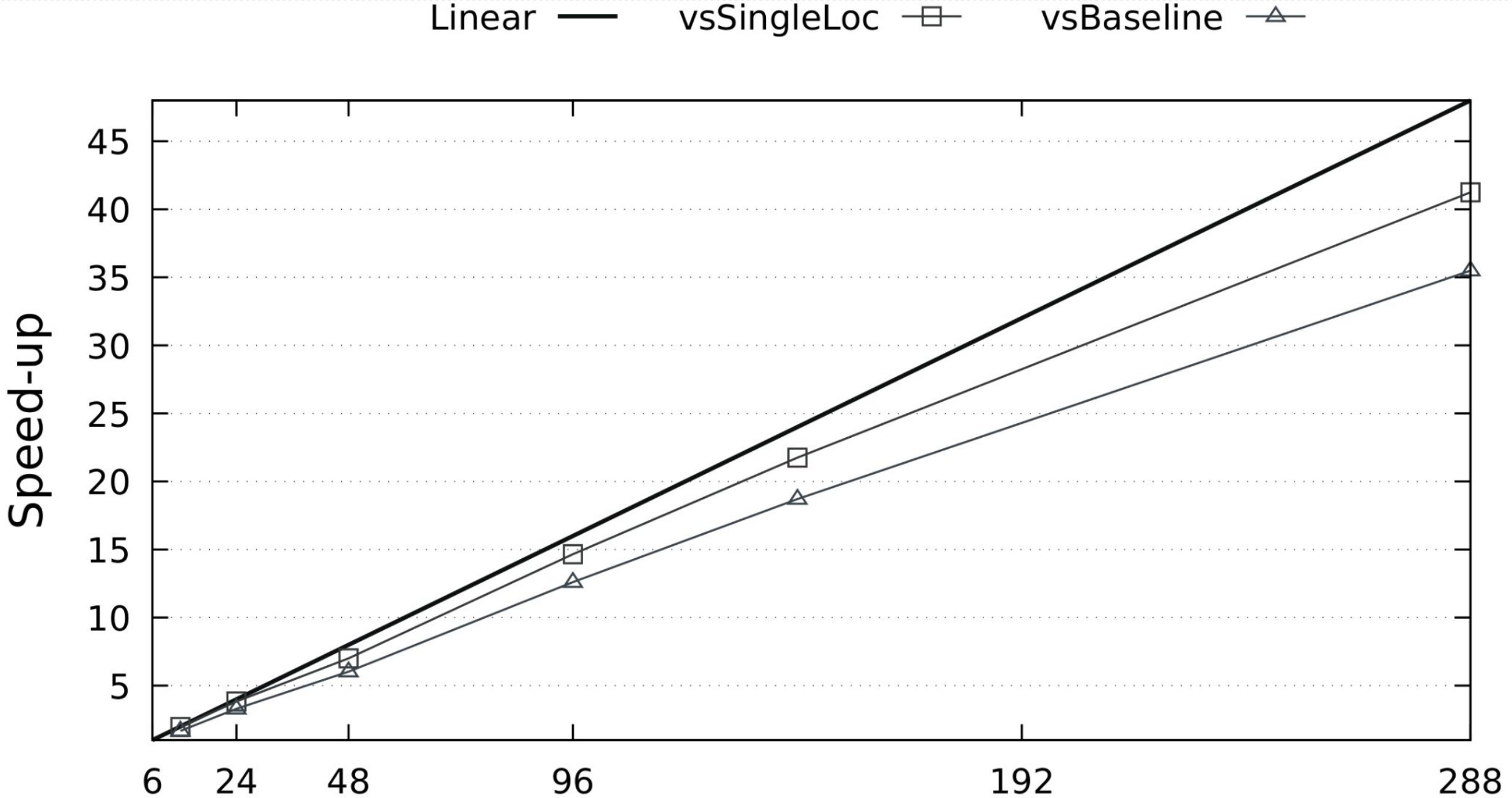
84% of the linear speedup vs. the same application on one computer node. 74% of the linear speedup vs. the optimized baseline in CUDA on one computer node. See Carneiro et al. (2021).
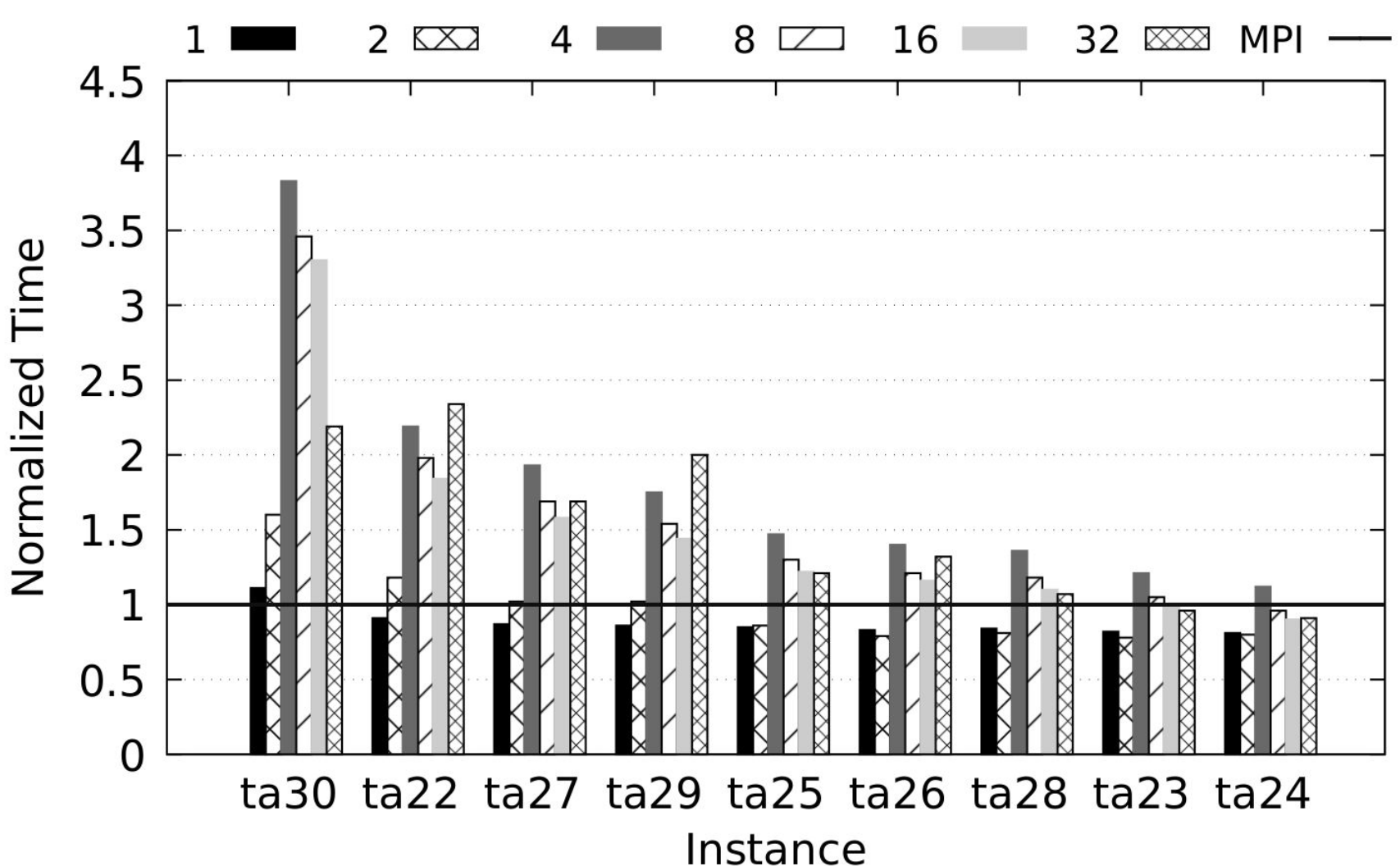
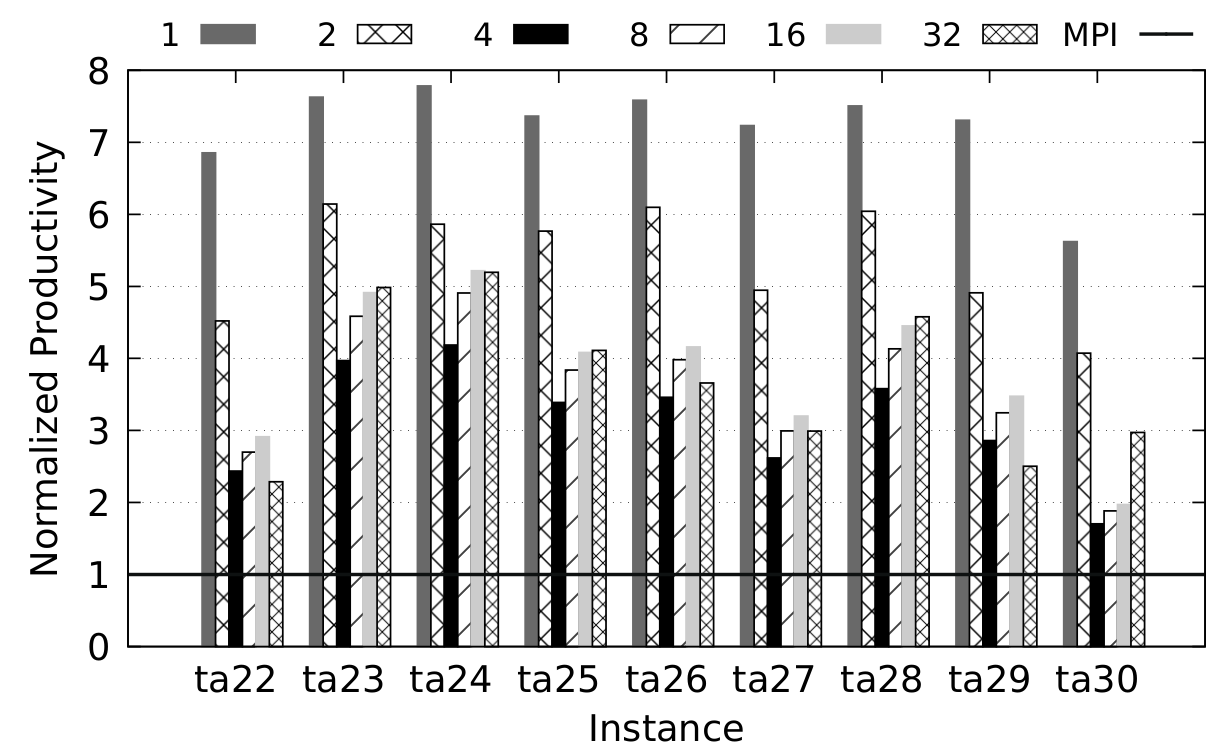
Some productivity/performance results of using Chapel for distributed exact optimization vs MPI+Cpp, flow-shop scheduling problem:
Execution times of Chapel-BB solving to the optimality Taillard instances ta21-30. The execution time is given relative to the MPI-PBB baseline. Next, normalized the productivity achieved by Chapel compared to its counterpart written in MPI+Cpp. Experiments executed on 1 (32 cores) to 32 nodes (1024 cores). For more details, see Carneiro et al. (2020).
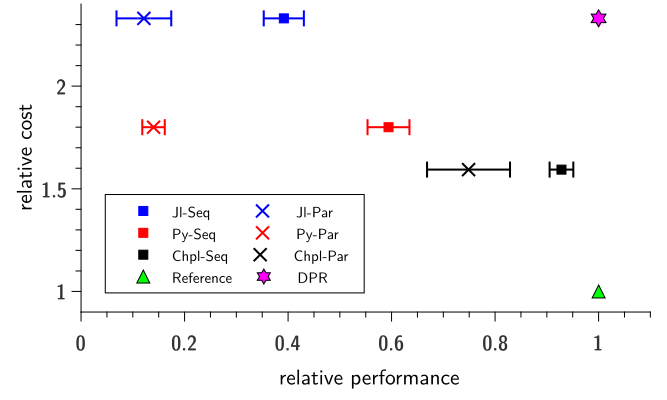
Illustration of the trade-off between relative cost and relative performance of three languages compared to the reference one. In the graph, the arrows point to the desired productivity region (DPR). The trade-off between relative cost and relative performance of Chapel, Julia, and Python compared to the reference implementation. In the graph, the desired productivity region (DPR) is on point 1.2.33. For more details, see Gmys et al. (2020).
-
Carneiro, T; Koutsantonis, L.; Melab, N.; Kieffer, E.; Bouvry, P. A Local Search for Automatic Parameterization of Distributed Tree Search Algorithms. PDCO 2022 - 12th IEEE Workshop Parallel / Distributed Combinatorics and Optimization, May 2022, Lyon, France.
-
Carneiro, T.; Melab, N.; Hayashi, A.; Sarkar, V. Towards Chapel-based Exascale Tree Search Algorithms: dealing withmultiple GPU accelerators. In: The International Conference on High Performance Computing & Simulation - HPCS2020 (2021). HPCS 2020 Outstanding Paper Award winner.
-
Carneiro, T.; Gmys, J.; Melab, N.; Tuyttens, D. Towards Ultra-scale Branch-and-Bound Using a High-productivity Lan-guage. Future Generation Computer Systems, 105: 196-209 (2020). DOI: 10.1016/J.future.2019.11.011.
-
Gmys, J.; Carneiro, T.; Melab, N.; Tuyttens, d.; Talbi, E-G. A Comparative Study of High-productivity High-performance Programming Languages for Parallel Metaheuristics. Swarm and Evolutionary Computation, 57:100720 (2020). DOI:10.1016/j.swevo.2020.100720
-
Carneiro, T.; Melab, N. An Incremental Parallel PGAS-based Tree Search Algorithm. In: The 2019 In-ternational Conference on High Performance Computing & Simulation - HPCS2019, pp.19-26, DOI:10.1109/HPCS48598.2019.9188106.
-
Carneiro, T.; Melab, N. Productivity-aware Design and Implementation of Distributed Tree-based Search Algorithms. In: The International Conference on Computational Science - ICCS2019. Lecture notes in computer science, vol.11536 (253-266), Springer. DOI: 10.1007/978-3-030-15996-2_2