-
Notifications
You must be signed in to change notification settings - Fork 5k
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Scratch 平台的神经网络(R 语言) #1867
Scratch 平台的神经网络(R 语言) #1867
Conversation
update20170706
|
校对认领 |
|
@lsvih 好的呢 🍺 |
|
|
||
| This post is for those of you with a statistics/econometrics background but not necessarily a machine-learning one and for those of you who want some guidance in building a neural-network from scratch in R to better understand how everything fits (and how it doesn’t). | ||
| 这篇文章是针对那些有着统计或经济学背景,却缺少机器学习知识,希望能够借助一些指导,通过 R 语言的 Scratch 平台更好的理解如何正确地使用机器学习。 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
->
这篇文章是为了那些有着统计或经济学背景,却缺少机器学习知识的人们所写,也是为了那些希望能够借助一些指导,通过 R 语言的 Scratch 平台更好地正确理解如何使用机器学习的人们所写。
这样还是有些不通顺,希望作者再看看怎么翻比较好
|
|
||
| This post is for those of you with a statistics/econometrics background but not necessarily a machine-learning one and for those of you who want some guidance in building a neural-network from scratch in R to better understand how everything fits (and how it doesn’t). | ||
| 这篇文章是针对那些有着统计或经济学背景,却缺少机器学习知识,希望能够借助一些指导,通过 R 语言的 Scratch 平台更好的理解如何正确地使用机器学习。 | ||
|
|
||
| Andrej Karpathy [wrote](https://medium.com/@karpathy/yes-you-should-understand-backprop-e2f06eab496b) that when CS231n (Deep Learning at Stanford) was offered: |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
删除原文
|
|
||
| Why bother with backpropagation when all frameworks do it for you automatically and there are more interesting deep-learning problems to consider? | ||
| 如果所有的反向传播算法已经被框架为你自动计算完毕了,你又何苦折磨自己而不去探寻更多有趣的深度学习问题呢? |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
->
如果框架已经为你自动计算完了所有的反向传播算法
|
|
||
| Starting from a linear regression we will work through the maths and the code all the way to a deep-neural-network (DNN) in the accompanying R-notebooks. Hopefully to show that very little is actually new information. | ||
| 从线性回归开始,借着 R 语言笔记,通过解决一系列的数学和编程问题直至深度神经网络(DNN)。希望能够显示出来你需要学习的新知识其实只有很少的一部分。 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
R 语言笔记 -> R-notebook
|
|
||
| 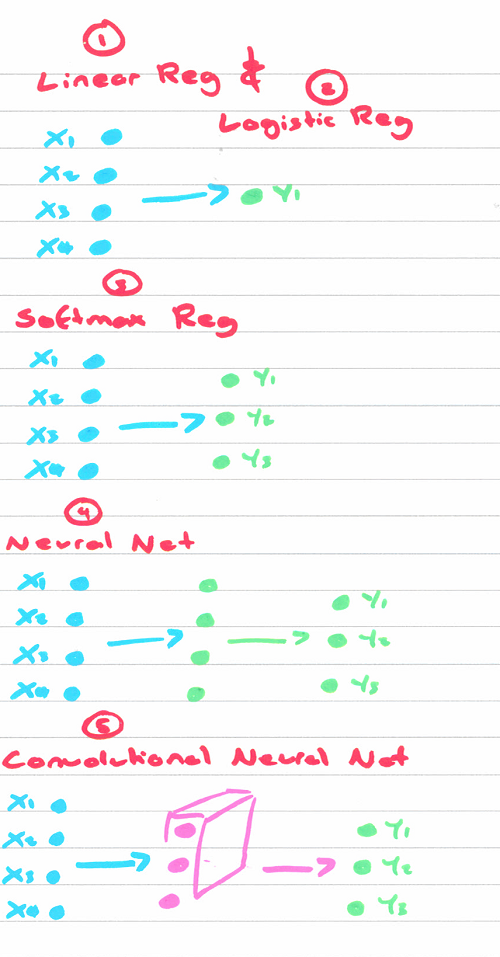 | ||
|
|
||
| **Notebooks:** | ||
| **笔记** |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Notebook:
// 这些都是 ipython notebook,感觉直接翻成笔记不太合适,不如保留原名,您觉得呢?下面的“笔记”同理。
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
感觉内容还是笔记,或者说 ipython notebook 有什么很特别的地方?这个我不是很清楚
| @@ -376,9 +377,10 @@ We can visualise this map with the following function: | |||
|
|
|||
|  | |||
|
|
|||
| Running this function we notice how computationally intensive the process is (compared to a standard fully-connected layer). If these feature maps are not useful ‘features’ (i.e. the loss is difficult to decrease when these are used) then back-propagation will mean we will get different weights which correspond to different feature-maps; which will become more useful to make the classification. | |||
| 在运行这个函数的时候我们意识到了整个过程是如何地高密度计算(与标准的全连接神经层相比)。如果这些 feature map 合不是那些那么有用的集合(也就是说,损失在被使用的时候很难被降低)然后反向传播会意味着我们将会得到不同的权重,与不同的 feature map 合相关联,对于构造聚类很有帮助。 | |||
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
,对于构造聚类很有帮助。 -> 。因此这个函数对于计算聚类很有用。
|
|
||
| filter_map <- lapply(X=c(1:64), FUN=function(x){ | ||
| # Random matrix of 0, 1, -1 | ||
| conv_rand <- matrix(sample.int(3, size=9, replace = TRUE), ncol=3)-2 | ||
| convolution(input_img = r_img, filter = conv_rand, show=FALSE, out=TRUE) | ||
| }) | ||
|
|
||
| We can visualise this map with the following function: | ||
| 我们可以用以下的函数可视化这个地图: |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
地图 -> map
|
|
||
| conv_emboss <- matrix(c(2,0,0,0,-1,0,0,0,-1), nrow = 3) | ||
| convolution(input_img = r_img, filter = conv_emboss) | ||
|
|
||
| You can check the notebook to see the result, however this seems to extract the edges from a picture. Other, convolutions can ‘sharpen’ an image, like this 3x3 filter: | ||
| 你可以查看笔记来看结果,然而这看起来是从图片中提取线段。否则,卷积可以‘尖锐化’一张图片,就像一个3*3的过滤器: |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
尖锐化 -> 锐化
|
|
||
| conv_emboss <- matrix(c(2,0,0,0,-1,0,0,0,-1), nrow = 3) | ||
| convolution(input_img = r_img, filter = conv_emboss) | ||
|
|
||
| You can check the notebook to see the result, however this seems to extract the edges from a picture. Other, convolutions can ‘sharpen’ an image, like this 3x3 filter: |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
笔记同上
|
|
||
| In the previous example we looked at a standard neural-net classifying handwritten text. In that network each neuron from layer i, was connected to each neuron at layer j — our ‘window’ was the whole image. This means if we learn what the digit “2” looks like; we may not recognise it when it is written upside down by mistake, because we have only seen it upright. CNNs have the advantage of looking at small bits of the digit “2” and finding patterns between patterns between patterns. This means that a lot of the features it extracts may be immune to rotation, skew, etc. For more detail, Brandon explains [here ](https://www.youtube.com/watch?v=FmpDIaiMIeA)what a CNN actually is in detail. | ||
| 在之前的例子中我们观察的是一个标准的神经网络对手写字体的归类。在神经网络中的 i 层的每个神经元,与 j 层的每个神经元相连-我们所框中的是整个图像(译者注:与 CNN 之前的5*5像素的框不同)。这意味着如果我们学习了数字2的样子,我们可能无法在它被错误地颠倒的时候识别出来,因为我们只见过它正的样子。CNN 在观察数字2的小的比特时并且在比较样式的时候有很大的优势。这意味着很多被提取出的特征对各种旋转,歪斜等是免疫的(译者注:即适用于所有变形)。对于更多的细节,Brandon 在[这里](https://www.youtube.com/watch?v=FmpDIaiMIeA)解释了什么是真正的 CNN。 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
数字中文空格
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
|
|
||
|  | ||
|
|
||
| **Notebooks:** | ||
| **笔记** |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
感觉内容还是笔记,或者说 ipython notebook 有什么很特别的地方?这个我不是很清楚
|
|
||
| When we have just two mutually-exclusive outcomes we would use a binomial logistic regression. With more than two outcomes (or “classes”), which are mutually-exclusive (e.g. this plane will be delayed by less than 5 minutes, 5–10 minutes, or more than 10 minutes), we would use a multinomial logistic regression (or “softmax”). In the case of many (n)classes that are not mutually-exclusive (e.g. this post references “R” and “neural-networks” and “statistics”), we can fit n-binomial logistic regressions. | ||
| 当我们只有两个互斥的结果时我们将使用一个二项逻辑回归。当候选结果(或者分类)多于两个时,即多项互斥(例如:这架飞机延误时间可能在5分钟内、5-10分钟或多于10分钟),我们将使用多项逻辑回归(或者“Softmax 回归”)(译者注:Softmax 函数是逻辑函数的一种推广,更多知识见[知乎](https://www.zhihu.com/question/23765351))。在这种情况下许多类别不是互斥的(例如:这篇文章中的“R”,“神经网络”和“统计学”),我们可以采用二项式逻辑回归(译者注:不是二项逻辑回归)。 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
这里我想强调的是 二项 与 二项式 的区别,主要防止读者马虎。你觉得怎样解释比较好呢?
| @@ -95,24 +94,24 @@ This can be implemented in R, like so: | |||
| beta_hat <- beta_hat - (lr*delta) | |||
| } | |||
|
|
|||
| Running this for 200 iterations gets us to same gradient and coefficient as the closed-form solution. Aside from being a stepping stone to a neural-network (where we use GD), this iterative method can be useful in practice when the the closed-form solution cannot be calculated because the matrix is too big to invert (to fit into memory). | |||
| 200次的迭代之后我们会得到和闭包方法一样的梯度与参数。除了这代表着我们的进步意外(我们使用了 GD),这个迭代方法在当闭包方法因矩阵过大而无法计算逆的时候也非常有用(因为有内存的限制)。 | |||
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
改成了 无法计算矩阵的逆 并加入了逗号断句,个人认为把具体原因解释出来会更清楚些
|
|
||
| 1. We use an ‘activation’/link function called the logistic-sigmoid to squash the output to a probability bounded by 0 and 1 | ||
| 2. Instead of minimising the quadratic loss we minimise the negative log-likelihood of the bernoulli distribution | ||
| 1. 我们使用一种称为 logistic-sigmoid 的 ‘激活’/链接函数来将输出压缩至0到1的范围内 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
这个意思就不一样了
|
|
||
| 1. We use an ‘activation’/link function called the logistic-sigmoid to squash the output to a probability bounded by 0 and 1 | ||
| 2. Instead of minimising the quadratic loss we minimise the negative log-likelihood of the bernoulli distribution | ||
| 1. 我们使用一种称为 logistic-sigmoid 的 ‘激活’/链接函数来将输出压缩至0到1的范围内 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
你可以看下 sigmoid 函数的图像,是一条连续的曲线,后面的二项分类还是要规定一条线的,这里的sigmoid只是产生0~1的数值
|
不等了,目前已有的校对意见有争议的讨论下,明天就 merge。 |
|
@CACppuccino sigmoid function 是我的错,看到 sigmoid 就直接相当然了 另外您本地改好之后麻烦 commit 一下哈 |
|
@sqrthree 根据校对者建议修改完毕 可以merge了 |
|
已经 merge 啦~ 快快麻溜发布到掘金专栏然后给我发下链接,方便及时添加积分哟。 |
|
@sqrthree 老哥你在一周前把这篇就给分享了。。我该怎么办 |
|
😄 发原创呀 |
请校对 @sqrthree #1856