-
Notifications
You must be signed in to change notification settings - Fork 32
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Turning around escape in model macro #311
Conversation
|
Can anyone help me think? I don't know how I broke macro expansion: julia> # Can't do that! Why?
julia> @macroexpand @model function demo4(n, ::Type{TV} = Vector{Float64}) where TV
m ~ Normal()
x = TV(undef, n)
@show __varinfo__
for i = eachindex(x)
x[i] ~ Normal(m, 1.0)
end
end
:($(Expr(:error, "malformed expression")))
julia> # Actually _calling_ the macro does work...
julia> var"@model"(LineNumberNode(1, nothing), Main, :(function demo4(n, ::Type{TV} = Vector{Float64}) where TV
m ~ Normal()
x = TV(undef, n)
@show __varinfo__
for i = eachindex(x)
x[i] ~ Normal(m, 1.0)
end
end))
:(#= /home/philipp/git/DynamicPPL.jl/src/compiler.jl:517 =# (Base).@__doc__ function demo4(n, ::Type{TV} = Vector{Float64}; ) where TV
#= line 1 =#
evaluator = ((__model__::Model, __varinfo__::AbstractVarInfo, __context__::DynamicPPL.AbstractContext, n, ::Type{TV}) where TV->begin
begin
#= REPL[127]:1 =#
#= REPL[127]:2 =#
begin
vn = (VarName){:m}()
inds = ()
isassumption = begin
let vn = (VarName){:m}()
if (DynamicPPL.contextual_isassumption)(__context__, vn)
if !((DynamicPPL.inargnames)(vn, __model__)) || (DynamicPPL.inmissings)(vn, __model__)
true
else
m === missing
end
else
false
end
end
end
if isassumption
m = (DynamicPPL.tilde_assume!)(__context__, (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(Normal()), vn)..., inds, __varinfo__)
else
if !((DynamicPPL.inargnames)(vn, __model__))
m = (DynamicPPL.getvalue_nested)(__context__, vn)
end
(DynamicPPL.tilde_observe!)(__context__, (DynamicPPL.check_tilde_rhs)(Normal()), m, vn, inds, __varinfo__)
end
end
#= REPL[127]:3 =#
x = TV(undef, n)
#= REPL[127]:4 =#
begin
Base.println("__varinfo__ = ", Base.repr(begin
#= show.jl:955 =#
local var"#310#value" = __varinfo__
end))
var"#310#value"
end
#= REPL[127]:6 =#
for i = eachindex(x)
vn = (VarName){:x}(((i,),))
inds = ((i,),)
isassumption = begin
let vn = (VarName){:x}(((i,),))
if (DynamicPPL.contextual_isassumption)(__context__, vn)
if !((DynamicPPL.inargnames)(vn, __model__)) || (DynamicPPL.inmissings)(vn, __model__)
true
else
#= /home/philipp/git/DynamicPPL.jl/src/compiler.jl:88 =# @views(x[i]) === missing
end
else
false
end
end
end
if isassumption
x[i] = (DynamicPPL.tilde_assume!)(__context__, (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(Normal(m, 1.0)), vn)..., inds, __varinfo__)
else
if !((DynamicPPL.inargnames)(vn, __model__))
x[i] = (DynamicPPL.getvalue_nested)(__context__, vn)
end
(DynamicPPL.tilde_observe!)(__context__, (DynamicPPL.check_tilde_rhs)(Normal(m, 1.0)), #= /home/philipp/git/DynamicPPL.jl/src/compiler.jl:88 =# @views(x[i]), vn, inds, __varinfo__)
end
end
end
end)
return (Model)(:demo4, evaluator, NamedTuple{(:n, :TV)}((n, TV)), NamedTuple{(:TV,)}((Vector{Float64},)))
end)
julia> # So does evaluation!
julia> var"@model"(LineNumberNode(1, nothing), Main, :(function demo4(n, ::Type{TV} = Vector{Float64}) where TV
m ~ Normal()
x = TV(undef, n)
@show __varinfo__
for i = eachindex(x)
x[i] ~ Normal(m, 1.0)
end
end)) |> eval
demo4 (generic function with 2 methods) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
It would be great to not have to escape everything. I actually tried to change it at some point but it turned out to be quite annoying and not completely straightforward (I don't remember why) so I did not complete or push these local changes.
|
So, what about the following approach:
I think that's all sound. It remains to check
julia> @macroexpand @model function demo4(n, x::Int)
m ~ Normal()
x = Vector(undef, n)
@show __varinfo__
for i in eachindex(x)
x[i] ~ Normal(m, 1.0)
end
end
quote
$(Expr(:meta, :doc))
function demo4(var"#402#n", var"#403#x"::DynamicPPL.Int; )
#= REPL[113]:1 =#
var"#401###evaluator#390" = ((var"#413#__model__"::Model, var"#414#__varinfo__"::AbstractVarInfo, var"#415#__context__"::DynamicPPL.AbstractContext, var"#402#n", var"#403#x"::DynamicPPL.Int)->begin
begin
#= REPL[113]:1 =#
#= REPL[113]:2 =#
begin
var"#404###vn#384" = (VarName){:m}()
var"#405###inds#385" = ()
var"#406###isassumption#386" = begin
if (DynamicPPL.contextual_isassumption)(var"#415#__context__", var"#404###vn#384")
if !((DynamicPPL.inargnames)(var"#404###vn#384", var"#413#__model__")) || (DynamicPPL.inmissings)(var"#404###vn#384", var"#413#__model__")
true
else
var"#407#m" === DynamicPPL.missing
end
else
false
end
end
if var"#406###isassumption#386"
var"#407#m" = (DynamicPPL.tilde_assume!)(var"#415#__context__", (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal()), var"#404###vn#384")..., var"#405###inds#385", var"#414#__varinfo__")
else
if !((DynamicPPL.inargnames)(var"#404###vn#384", var"#413#__model__"))
var"#407#m" = (DynamicPPL.getvalue_nested)(var"#415#__context__", var"#404###vn#384")
end
(DynamicPPL.tilde_observe!)(var"#415#__context__", (DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal()), var"#407#m", var"#404###vn#384", var"#405###inds#385", var"#414#__varinfo__")
end
end
#= REPL[113]:3 =#
var"#403#x" = DynamicPPL.Vector(DynamicPPL.undef, var"#402#n")
#= REPL[113]:4 =#
begin
Base.println("__varinfo__ = ", Base.repr(begin
#= show.jl:955 =#
local var"#408##400#value" = var"#414#__varinfo__"
end))
var"#408##400#value"
end
#= REPL[113]:5 =#
for var"#409#i" = DynamicPPL.eachindex(var"#403#x")
var"#410###vn#387" = (VarName){:x}(((var"#409#i",),))
var"#411###inds#388" = ((var"#409#i",),)
var"#412###isassumption#389" = begin
if (DynamicPPL.contextual_isassumption)(var"#415#__context__", var"#410###vn#387")
if !((DynamicPPL.inargnames)(var"#410###vn#387", var"#413#__model__")) || (DynamicPPL.inmissings)(var"#410###vn#387", var"#413#__model__")
true
else
(Base.maybeview)(var"#403#x", var"#409#i") === DynamicPPL.missing
end
else
false
end
end
if var"#412###isassumption#389"
var"#403#x"[var"#409#i"] = (DynamicPPL.tilde_assume!)(var"#415#__context__", (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal(var"#407#m", 1.0)), var"#410###vn#387")..., var"#411###inds#388", var"#414#__varinfo__")
else
if !((DynamicPPL.inargnames)(var"#410###vn#387", var"#413#__model__"))
var"#403#x"[var"#409#i"] = (DynamicPPL.getvalue_nested)(var"#415#__context__", var"#410###vn#387")
end
(DynamicPPL.tilde_observe!)(var"#415#__context__", (DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal(var"#407#m", 1.0)), (Base.maybeview)(var"#403#x", var"#409#i"), var"#410###vn#387", var"#411###inds#388", var"#414#__varinfo__")
end
end
end
end)
return (Model)($(QuoteNode(:($(Expr(:escape, :demo4))))), var"#401###evaluator#390", DynamicPPL.NamedTuple{(:n, :x)}((var"#402#n", var"#403#x")), DynamicPPL.NamedTuple())
end
endNote that a lot of names are "double gensymed", since they are gensyms undergoing hygiene. |
|
Sounds good, we should rely on the default hygiene as much as possible. It seems in the example the argument types should be |
src/compiler.jl
Outdated
| # as the default conditioning. Then we no longer need to check `inargnames` | ||
| # since it will all be handled by `contextual_isassumption`. | ||
| if !($(DynamicPPL.inargnames)($vn, __model__)) || | ||
| $(DynamicPPL.inmissings)($vn, __model__) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
[JuliaFormatter] reported by reviewdog 🐶
| $(DynamicPPL.inmissings)($vn, __model__) | |
| $(DynamicPPL.inmissings)($vn, __model__) |
|
It seems something went wrong and the deprecated internal names where reintroduced when you merged the master branch. |
|
Right, I didn't realize you had removed them already :D |
|
I think this looks good: julia> @macroexpand @model function demo4(n, ::Type{T}; σ) where {T}
m ~ Normal()
x = Vector{T}(undef, n)
for i in eachindex(x)
x[i] ~ Normal(m, σ)
end
return (;m, x, ℓ = getlogp(__varinfo__))
end
quote
function demo4(var"#176#__model__"::Model, var"#177#__varinfo__"::AbstractVarInfo, var"#178#__context__"::DynamicPPL.AbstractContext, var"#179#n", ::DynamicPPL.Type{var"#182#T"}, var"#181#σ"; ) where var"#182#T"
#= REPL[11]:1 =#
begin
#= REPL[11]:1 =#
#= REPL[11]:2 =#
begin
var"#167###vn#295" = (VarName){:m}()
var"#168###inds#296" = ()
var"#169###isassumption#297" = begin
if (DynamicPPL.contextual_isassumption)(var"#178#__context__", var"#167###vn#295")
if !((DynamicPPL.inargnames)(var"#167###vn#295", var"#176#__model__")) || (DynamicPPL.inmissings)(var"#167###vn#295", var"#176#__model__")
true
else
var"#170#m" === DynamicPPL.missing
end
else
false
end
end
if var"#169###isassumption#297"
var"#170#m" = (DynamicPPL.tilde_assume!)(var"#178#__context__", (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal()), var"#167###vn#295")..., var"#168###inds#296", var"#177#__varinfo__")
else
if !((DynamicPPL.inargnames)(var"#167###vn#295", var"#176#__model__"))
var"#170#m" = (DynamicPPL.getvalue_nested)(var"#178#__context__", var"#167###vn#295")
end
(DynamicPPL.tilde_observe!)(var"#178#__context__", (DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal()), var"#170#m", var"#167###vn#295", var"#168###inds#296", var"#177#__varinfo__")
end
end
#= REPL[11]:3 =#
var"#171#x" = DynamicPPL.Vector{var"#182#T"}(DynamicPPL.undef, var"#179#n")
#= REPL[11]:4 =#
for var"#172#i" = DynamicPPL.eachindex(var"#171#x")
var"#173###vn#298" = (VarName){:x}(((var"#172#i",),))
var"#174###inds#299" = ((var"#172#i",),)
var"#175###isassumption#300" = begin
if (DynamicPPL.contextual_isassumption)(var"#178#__context__", var"#173###vn#298")
if !((DynamicPPL.inargnames)(var"#173###vn#298", var"#176#__model__")) || (DynamicPPL.inmissings)(var"#173###vn#298", var"#176#__model__")
true
else
(Base.maybeview)(var"#171#x", var"#172#i") === DynamicPPL.missing
end
else
false
end
end
if var"#175###isassumption#300"
var"#171#x"[var"#172#i"] = (DynamicPPL.tilde_assume!)(var"#178#__context__", (DynamicPPL.unwrap_right_vn)((DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal(var"#170#m", var"#181#σ")), var"#173###vn#298")..., var"#174###inds#299", var"#177#__varinfo__")
else
if !((DynamicPPL.inargnames)(var"#173###vn#298", var"#176#__model__"))
var"#171#x"[var"#172#i"] = (DynamicPPL.getvalue_nested)(var"#178#__context__", var"#173###vn#298")
end
(DynamicPPL.tilde_observe!)(var"#178#__context__", (DynamicPPL.check_tilde_rhs)(DynamicPPL.Normal(var"#170#m", var"#181#σ")), (Base.maybeview)(var"#171#x", var"#172#i"), var"#173###vn#298", var"#174###inds#299", var"#177#__varinfo__")
end
end
#= REPL[11]:7 =#
return (; m = var"#170#m", x = var"#171#x", ℓ = DynamicPPL.getlogp(var"#177#__varinfo__"))
end
end
begin
$(Expr(:meta, :doc))
function demo4(var"#183#n", ::DynamicPPL.Type{var"#185#T"}; σ) where var"#185#T"
#= REPL[11]:1 =#
return (Model)(:demo4, demo4, DynamicPPL.NamedTuple{(:n, :T, :σ)}((var"#183#n", var"#185#T", σ)), DynamicPPL.NamedTuple())
end
end
end
julia> @model function demo4(n, ::Type{T}; σ) where {T}
m ~ Normal()
x = Vector{T}(undef, n)
for i in eachindex(x)
x[i] ~ Normal(m, σ)
end
return (;m, x, ℓ = getlogp(__varinfo__))
end
demo4 (generic function with 2 methods)
julia> methods(demo4)
# 2 methods for generic function "demo4":
[1] demo4(__model__::Model, __varinfo__::AbstractVarInfo, __context__::DynamicPPL.AbstractContext, n, ::Type{var"#201#T"}, σ) where var"#201#T" in Main at REPL[12]:1
[2] demo4(n, ::Type{var"#204#T"}; σ) where var"#204#T" in Main at REPL[12]:1
julia> demo4(2, Float64; σ = 1.0)
Model{typeof(demo4), (:n, :T, :σ), (), (), Tuple{Int64, DataType, Float64}, Tuple{}, DefaultContext}(:demo4, demo4, (n = 2, T = Float64, σ = 1.0), NamedTuple(), DefaultContext())
julia> demo4(2, Float64; σ = 1.0)()
(m = 0.1242670570655595, x = [0.38638092732182805, -0.08489833515866964], ℓ = -2.820763671492404)
|
|
I managed to fix the error by making sure that the arguments and where clause of the |
|
I also noticed that the example above is not what we want. Eg., |
|
But you're right about the global variables needed to be resolved in calling scope. I have to think about that. The bug is resolved to some extent by escaping arguments and where-params in that the syntax error does not occur anymore, but then we'd also have to escape all occurences of them in the body (due to the problem admitted in the previous paragraph), which is tedious and should not be necessary in the first place, IMO! I am convinced there is some underlying problem in either hygiene or MacroTools, or how we change the meaning of |
Sure, but often this is sufficient if you construct an unescaped macro expression. E.g., in the rule definition macros in ChainRulesCore (https://github.com/JuliaDiff/ChainRulesCore.jl/blob/3b46ac592fcb6bce8377f45ba2f9f5a4321a0bdf/src/rule_definition_tools.jl#L172-L177 and similar lines) rely on this behaviour - the interpolation was removed on purpose when the macro was changed to an unescaped version. However, I guess here it might be problematic in the function body if e.g. users use variables of name
I believe there's no way around this issue other than escaping all user-provided statements in the function body. The question is what we gain in the end then, in particular if we still interpolate
The interesting thing is that it is only necessary to escape it in |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference): 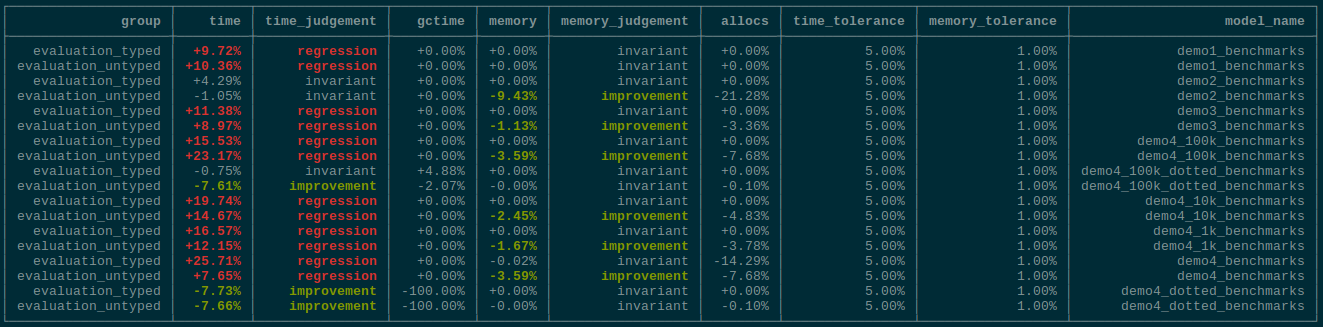 The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Hygiene on |
|
OK, so there's a few difficulties...
sooo... I guess it isn't really worth it? @torfjelde @devmotion, what do you think? |
|
Yes, unfortunately it seems somewhat between impossible and very difficult/annoying, so I think it's maybe not worth it. Just wanted to mention that the fix for
(JuliaLang/julia#42220) was backported to Julia 1.6.4, so it's fixed in the latest stable release 🙂 |
I came to the same conclusion. We are just doing things for which hygiene is not the right thing: messing around within the passed expression. |
Instead of
escaping the whole generated code andgensyming internal names ourselves, escape only what is necessary and hygiene do its work.Implements #308. Just a first try, I'm not even sure yet what to keep.