-
Notifications
You must be signed in to change notification settings - Fork 32
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
[Merged by Bors] - Sibling PR of introduction of Setfield.jl in AbstractPPL.jl #295
Conversation
| @@ -271,6 +293,10 @@ function generate_mainbody!(mod, found, expr::Expr, warn) | |||
| # Do not touch interpolated expressions | |||
| expr.head === :$ && return expr.args[1] | |||
|
|
|||
| # Do we don't want escaped expressions because we unfortunately | |||
| # escape the entire body afterwards. | |||
| Meta.isexpr(expr, :escape) && return generate_mainbody(mod, found, expr.args[1], warn) | |||
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Because we do the wrong thing and escape the entire body of the method in @model, we cannot handle nested escaping. And since Setfield.lensmacro does the right thing, only escaping what it needs to, we run into issues.
This is a hack to essentially ensure that any escaping will be removed. Note that this doesn't break anything because before we couldn't even use escaped expressions within @model, and so I think it's fine for this PR alone. BUT we should really address this properly, i.e. rewrite @model to only escape what it needs to.
src/compiler.jl
Outdated
| ) | ||
| ) | ||
|
|
||
| return remove_escape(setmacro(identity, expr, overwrite=true)) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Same as above. setmacro correctly escapes, we don't, and so we hack.
src/compiler.jl
Outdated
| @assert length(ex.args) == 2 | ||
| ref, val = ex.args | ||
| obj, lens = Setfield.parse_obj_lens(ref) | ||
| lens_var = gensym("lens") |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
This is essentially copy-paste from Setfields' implementation, but we add this in here.
I believe this will also be sorted out if we fix the "escape EVERYTHING" in @model since then lens should automatically be assigned a unique symbol expanded.
If not we should just make a PR to Setfield.jl. Using gensym seems like it loses nothing.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Regarding my above comment about setmacro: if we have copied the function to here anyway, we might as well rename it to something more descriptive.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Agree with that, though my intention is to make a PR to Setfield.jl now that we seem to be going in the direction of using it.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Co-authored-by: github-actions[bot] <41898282+github-actions[bot]@users.noreply.github.com>
|
@phipsgabler :) |
…/DynamicPPL.jl into tor/allow-non-array-variables
src/compiler.jl
Outdated
| ) | ||
| ) | ||
|
|
||
| return remove_escape(setmacro(identity, expr; overwrite=true)) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
expr -> setmacro(idendity, expr; overwrite=true) deserves its own function name... This is pretty opaque, IMHO, if you haven't just before read the source of Setfield.jl.
src/compiler.jl
Outdated
| @assert length(ex.args) == 2 | ||
| ref, val = ex.args | ||
| obj, lens = Setfield.parse_obj_lens(ref) | ||
| lens_var = gensym("lens") |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Regarding my above comment about setmacro: if we have copied the function to here anyway, we might as well rename it to something more descriptive.
src/compiler.jl
Outdated
| @@ -38,7 +38,7 @@ isassumption(expr) = :(false) | |||
|
|
|||
| # If we're working with, say, a `Symbol`, then we're not going to `view`. | |||
| maybe_view(x) = x | |||
| maybe_view(x::Expr) = :($(DynamicPPL.maybe_unwrap_view)(@view($x))) | |||
| maybe_view(x::Expr) = :($(DynamicPPL.maybe_unwrap_view)(@views($x))) | |||
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
@views is now needed since we can have property-access, etc. in x.
|
I just did some benchmarks and it's a bit inconclusive, though the variations are small.
We're talking miniscule differences though, so uncertain if we even care or can conclude anything from this 🤷 EDIT: I figured it out. It was because EDIT 2: See the description of the PR for up-to-date benchmarks. |
|
bors r+ |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference): 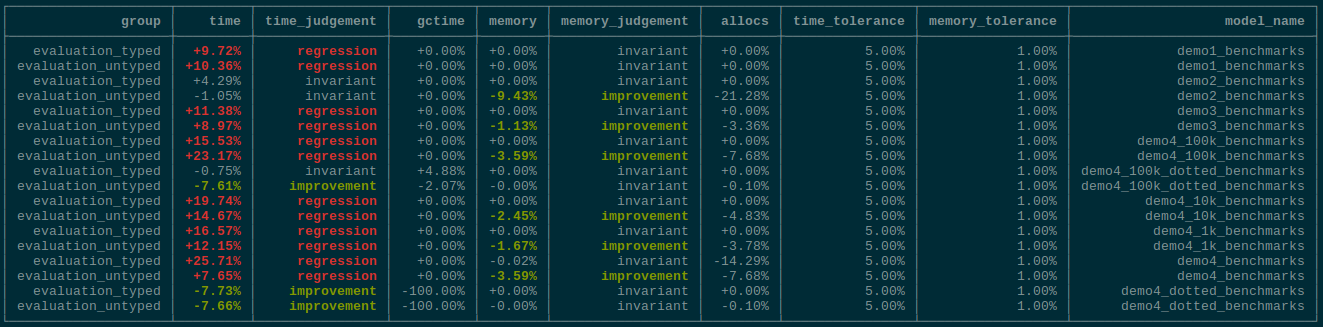 The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Build failed: |
|
bors r+ |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Build failed: |
|
bors r+ |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Build failed: |
test/compiler.jl
Outdated
| @@ -178,7 +183,7 @@ end | |||
| @model function testmodel_missing3(x) | |||
| x[1] ~ Bernoulli(0.5) | |||
| global varinfo_ = __varinfo__ | |||
| global sampler_ = __context__.sampler | |||
| global sampler_ = __context__.s2ampler | |||
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I guess this should be
| global sampler_ = __context__.s2ampler | |
| global sampler_ = __context__.sampler |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Nono, that was fully intended. I forgot to mention that while you were gone we renamed the sampler field for SamplingContext to s2ampler. I thought it looked cooler 😎
|
bors r+ |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Build failed: |
|
bors r+ |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):  The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
|
Pull request successfully merged into master. Build succeeded: |
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff.
We also finally drop the passing of the
indsaround in the tilde-pipeline, which is not very useful now that we have the more general lenses inVarName.TODOs:
DeprecateEDIT: On second thought, let's not. See comment for reason.*tilde_*withindsargument appropriately.(Maybe) RewriteDeferred to Turning around escape in model macro #311@modelto not escape the entire expression.hashforTuplevs.hashfor immutable struct 😕Sample fields of structs
Sample fields of
DataFrameBenchmarks
Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference):
The weird thing is that we're using less memory, indicating that type-inference might better?
0.31.1
0.31.1
Setup
using BenchmarkTools, DynamicPPL, Distributions, SerializationModels
demo1results["evaluation_untyped"]results["evaluation_typed"]demo2results["evaluation_untyped"]results["evaluation_typed"]demo3results["evaluation_untyped"]results["evaluation_typed"]demo4: loads of indexingresults["evaluation_untyped"]results["evaluation_typed"]results["evaluation_untyped"]results["evaluation_typed"]This PR
This PR
Setup
using BenchmarkTools, DynamicPPL, Distributions, SerializationModels
demo1results["evaluation_untyped"]results["evaluation_typed"]demo2results["evaluation_untyped"]results["evaluation_typed"]demo3results["evaluation_untyped"]results["evaluation_typed"]demo4: lots of univariate random variablesresults["evaluation_untyped"]results["evaluation_typed"]results["evaluation_untyped"]results["evaluation_typed"]